Представление выражений с помощью деревьев

 

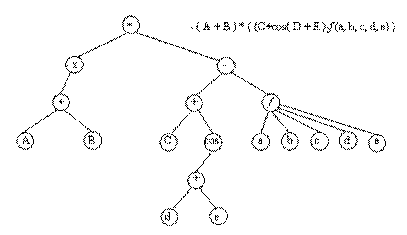
С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу операция. В общем случае дерево при этом может оказаться не бинарным (см. рис.7).

 

Рис.7. Представление арифметического выражения произвольного вида в виде дерева.

 

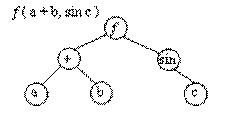
Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным (см. рис.8).

 

Рис. 8. Представление арифметического выражения в виде бинарного дерева

 

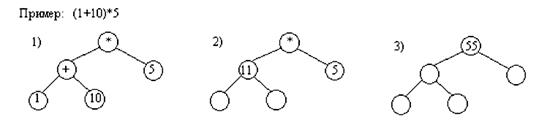
Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.

Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения (см. рис.9).

 

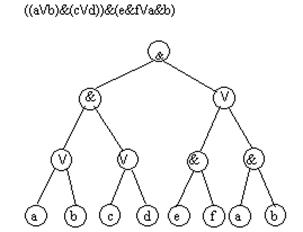
Рис.9. Вычисление арифметического выражения с помощью бинарного дерева

Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным (см. рис.10).

Рис. 10. Представление логического выражения в виде бинарного дерева

Контрольные вопросы

 

1) Понятие дерева, двоичного дерева, упорядоченного дерева, дерева поиска.

2) Способы задания дерева.

3) Способы обхода дерева (в глубину: прямой, обратный, симметричный; в ширину).

4) Показать, что бинарное дерево можно построить, если заданы прямой и обратный порядки расположения его узлов. Можно ли это сделать, если заданы прямой и концевой порядки? Если заданы обратный и симметричный порядки?

5) Найдите все бинарные деревья, узлы которых располагаются точно в одной и той же последовательности

а) в прямом и обратном порядках;

б) в прямом и симметричном порядках;

в) в обратном и симметричном порядках.

6) Каково наибольшее число вершин, находящихся одновременно в стеке при обходе двоичного дерева, содержащего n элементов:

а) в прямом,

б) обратном,

в) симметричном порядках?

Задания для практической работы

 

Во всех задачах тип значений элементов дерева простой. Исходное дерево после ввода распечатать в одном из порядков.

1. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения при прямом обходе дерева.

2. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения при обратном обходе дерева.

3. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения при концевом обходе дерева.

4. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения реализуя обход, рекурсивно.

5. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева при прямом обходе дерева.

6. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева при обратном обходе дерева.

7. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева при концевом обходе дерева.

8. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева реализуя обход, рекурсивно.

9. В заданном непустом бинарном дереве найти длину (число ветвей) пути от корня до ближайшей вершины со значением равным заданному при прямом обходе дерева;

10. В заданном непустом бинарном дереве найти длину (число ветвей) пути от корня до ближайшей вершины со значением равным заданному реализуя обход, рекурсивно.

11. В заданном непустом бинарном дереве подсчитать число вершин на n- ом уровне, считая корень вершиной 0-го уровня.

12. Задано бинарное дерево. Определить, есть ли в этом дереве хотя бы два одинаковых элемента.

13. Распечатать все элементы заданного непустого бинарного дерева по уровням: сначала из корня дерева, затем (слева направо) из вершин, дочерних по отношению к корню, затем (слева направо) из вершин, дочерних по отношению к этим вершинам, и т.д.

14. Формулу вида:

< формула >::= < терминал >|(< формула > < знак > < формула >)

< знак >::= + | - | *

< терминал >::= 0|1|2|3|4|5|6|7|8|9 можно представить в виде двоичного дерева (‘дерева – формулы ‘):

- формула из одного терминала (цифры) представляется деревом из одной вершины (корнем) с этим терминалом;

- формула вида (f₁ s f₂) - деревом, в котором корень – это знак s, а левое и правое поддеревья – это соответствующие представления f₁ и f₂:

а) по заданной формуле построить дерево – формулу, обходя дерево – формулу в 1)прямом, 2)обратном, 3)концевом порядке, напечатать его элементы и вычислить (как целое число) значение;

б) проверить, является ли заданное двоичное дерево (с элементами типа char) деревом – формулой и напечатать его элементы в порядке 1)прямого, 2)обратного, 3)концевого обхода;

в) пусть в дереве – формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных; преобразовать заданное дерево – формулу, заменяя в нем все поддеревья, соответствующие формулам ((f₁ ± f₂) * f₃) и(f₁ *(f₂ ± f₃)) на поддеревья, соответствующие формулам  ((f₁ * f₃) ± (f₂ * f₃)) и ((f₁ * f₂) ± (f₁ * f₃)); распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке;

г) выполнить в заданном дереве – формуле преобразования, обратные преобразованиям из пункта в; распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

15. Заданную последовательность из строчных латинских букв, оканчивающуюся точкой, представить в виде дерева поиска, затем преобразовать его, удалив символ с наименьшим значением. Распечатать  преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

16. Заданную последовательность из строчных латинских букв, оканчивающуюся точкой, представить в виде дерева поиска, затем преобразовать его, удалив символ с наибольшим значением. Распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

17. Заданную последовательность целых чисел, оканчивающуюся нулем, представить в виде дерева поиска, затем преобразовать его, добавив еще одно целое число; распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

Литература

 

1. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. – М.:Вильямс, 2000. – 382 с.

2. Вирт Н. Алгоритмы и структуры данных: Пер. с англ. — 2-е изд. испр. - СПб.: Невский Диалект, 2001. -352 с.

3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики: Пер. с англ. — М.: Мир, 1998, —703с.

4. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, 2001 — 960 с.

5. Кнут Д. Искусство программирования. Т.1. – М.: Вильямс, 2000 – 690с.

6. Кнут Д. Искусство программирования. Т.2. – М.: Вильямс, 2000 – 788с.

1. Кнут Д. Искусство программирования. Т.3. – М.: Вильямс, 2000 – 800с.
2. Кубенский А. А. Структуры и алгоритмы обработки данных: объектно-ориентированный подход и реализация на C++. - СПб.: БХВ-Петербург, 2004. - 464с.

9. Липский В. Комбинаторика для программистов: Пер. с польск. М.: Мир, 1988. —213 с.

1. Мозговой М.В. Классика программирования: алгоритмы, языки, автоматы, компиляторы. Практический подход. — СПб.: Наука и Техника, 2006.— 320 с.
2. Седжвик Р., Фундаментальные алгоритмы на C++. Анализ/Структуры данных/Сортировка/Поиск: Пер. с англ./Роберт Седжвик. - К.: Издагсльство «ДиаСофт», 2001.- 688 с.
3. Хэзфидд Ричард, Кирби Лоуренс и др. Искусство программирования на С. Фундаментальные алгоритмы, структуры данных и примеры приложений. Энциклопедия программиста: Пер. с англ./Ричард Хэзфилд, Лоуренс Кирби и др. — К.: Издательство «ДиаСофт», 2001. — 736 с.