Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции автомобиля относительно поперечной осиСодержание книги
Поиск на нашем сайте
При оценке плавности хода, устойчивости и управляемости автомобилей необходимо знать величину момента инерции автомобиля относительно его поперечной оси У~У,проходящей через центр его тяжести. В курсе "Теория автомобиля" известны несколько способов его определения: по колебаниям подвешенного автомобиля; по его колебаниям на подпружиненной качающейся платформе; подвешиванием его на пружине над одной из осей. Для ознакомления студентов с одним из методов (например, на подпружиненной качающейся платформе) служит настоящая лабораторная работа.
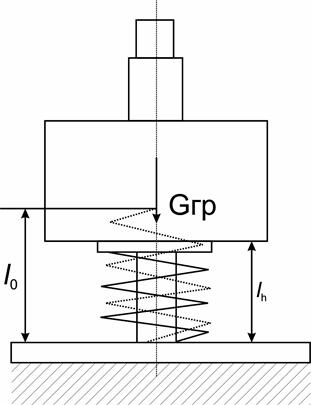
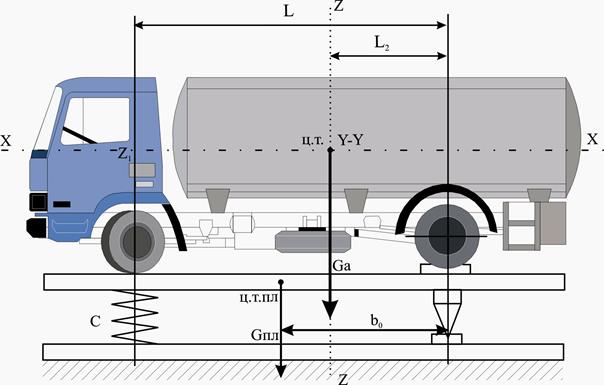
Приборы и оборудование 1. Модель автомобиля. 2. Стенд "качающаяся платформа". 3. Прибор для определения жесткости пружин. 4. Секундомер. 5. Весы циферблатные с пределом 0...I кг. 6. Линейка масштабная. 7. Микрокалькулятор. 8. Отвес. Для определения момента инерции модели относительно ее поперечной оси, проходящей через его центр тяжести, на качающейся подпружиненной платформе необходимо предварительно определить положение центра тяжести модели способом, изложенным в лабораторной работе №1 (величину l 2), взвесить отдельно платформу и модель на весах с точностью до 10 г и найти жесткость пружины качающейся платформы. Жесткость пружины, установленной под платформу, может быть определена замером ее длины в свободном состоянии и под нагрузкой определенной величины, например 10Н, из соотношения С=Gгр / (l0 – lн) (11) где С - жесткость пружины, Н/м; l0 -длина пружины в свободном состоянии, м; lн - длина пружины под нагрузкой, м; Gгр - вес груза, Н. Располагая величиной массы платформы и модели, можно найти момент инерции модели относительно ее поперечной оси. Порядок выполнения работы 1. Найти центр тяжести платформы путем двукратного ее подвешивания в разных точках одновременно с отвесом. Точка пересечения вертикалей, проведенных из точки подвеса по нити, - центр тяжести платформы. 2. Замерить масштабной линейкой расстояние от центра тяжести платформы до оси качания b 0 (рис.3). 3. Замерить масштабной линейкой базу L модели (межосевое расстояние). 4. Установить платформу на ось качания, а под нее на расстоянии L, равном базе модели, пружину, стараясь расположить ее на равном удалении от опор качания платформы, т.е. на продольной оси модели (рис.4).
5. Определить момент инерции платформы Jпл. Для этого необходимо дать ей возможность совершать свободные колебания относительно опор качания, сжав и отпустив пружину под платформой. Разделив время Σt на число колебаний платформы, в течение которых она их совершит, определяют период колебаний платформы. Опыт повторяют трижды. Из уравнения определяют искомую величину Jпл:
где Jпл- момент инерции платформы, Нмс2, С - жесткость пружины, Н/м; L -база модели, м; Gпл - вес платформы, Н; b0 - расстояние от центра тяжести платформы до ее оси качания; Tпл ср - средний период колебаний платформы, с. 6. Определить положение центра тяжести модели относительно одной из осей L2 способом, описанным в лабораторной работе №1 или узнать у преподавателя. 7. Установить модель на платформу таким образом, чтобы ее задняя ось совпадала с осью качания платформы, а середина передней оси находилась над пружиной, которая располагается под платформой.
Рис. 3 Схема определения жесткости пружин
Рис. 4 Схема установки автомобиля на платформу
8. Определить период свободных колебаний системы "модель-платформа", сообщив ей колебательное движение и замерив время и число совершенных за этот срок колебаний. Опыт повторяют трижды. 9. Определить момент инерции модели относительно ее поперечной оси по уравнению:
где Jм-момент инерции модели, Нмс, Tc - средний период колебаний системы "модель-платформа" в трех опытах, с; Ga.- вес модели, Н. 10. Результаты измерений и вычислений заносят в табл.3.1 Табл. 3.1
Лабораторная работа №4 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ φ y И νпоп АВТОМОБИЛЕЙ НА КОСОГОРЕ Поперечная устойчивость на косогоре автомобилей оказывает существенное влияние на их безопасность, так как автомобили с большим значением ν поп могут двигаться по косогорам с относительно большими скоростями и совершать маневры. Помочь будущему инженеру-механику составить представление о количественной стороне поперечной устойчивости автомобилей могут лабораторные работы с их моделями.
Приборы и оборудование 1. Модель автомобиля. 2. Штангенциркуль. 3. Стол с изменяемой величиной угла поперечного наклона. 4. Линейка масштабная. 5. Набор площадок под модель из различных материалов: деревянная, стеклянная, пластмассовая, стальная и покрытая наждачной бумагой. 6. Микрокалькулятор. 7. Набор грузов для модели. 8. Весы циферблатные.
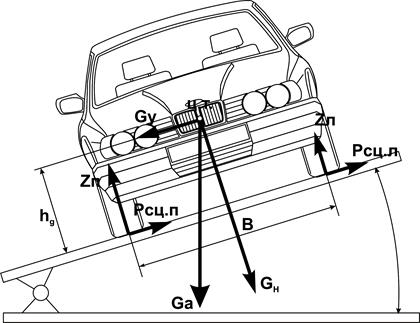
Порядок выполнения работы Поперечная устойчивость машин на косогоре определяется способностью находится на нем (двигаться или стоять) без соскальзывания или опрокидывания. Количественно поперечную устойчивость можно оценить с помощью двух коэффициентов коэффициента сцепления движетеля с опорной поверхностью в поперечном направлении φy и коэффициента поперечной устойчивости ν поп. В момент потери моделью поперечной устойчивости на нее действуют следующие силы (рис. 5): Gа - вес модели, Н; GH-нормальная составляющая веса, Н; Gy - поперечная составляющая силы веса, Н; Pсц-поперечная силы сцепления движетелей (колес, гусениц) модели с опорной поверхностью, Н. Соотношения между этими величинами выражаются уравнениями:
В случае соскальзывания модели с наклонной поверхности
После исключения веса модели Ga. и в случае опрокидывания модели
Соотношения (14) и (15) позволяют определить порядок выполнения лабораторной работы.
Рис.5 Определение поперечной устойчивости автомобиля
1. Взвесить модель незагруженной. 2. Определить высоту центра тяжести модели незагруженной способом, описанным в лабораторной работе №1. 3. Проделать то же с различными грузами и занести данные в таблицу результатов испытаний. 4. Установить на стол с изменяемым углом наклона площадку из стекла в горизонтальном положении, а на нее модель параллельно оси вращения опорной площадки. 5. Постепенно, вращая винт регулировки наклона опорной площадки стола, увеличивать угол наклона до тех пор, пока не произойдет потеря его поперечной устойчивости (соскальзывание или опрокидывание). 6. Замерить угол βнаклона опорной поверхности в момент потери моделью поперечной устойчивости и занести результаты занести в табл. 4.1. 7. Проделать то же самое для другой площадки (стальной, пластмассовой, резиновой и т.п.) при других значениях высоты центра тяжести модели hg. 8. Величины дополнительных грузов и тип покрытия опорной поверхности задается преподавателем. 9. Вычислить по уравнениям (14) и (15) (в зависимости от того, какой вид потери поперечной устойчивости произошел: опрокидывание или соскальзывание) величину νпопили φy и сравнить их с данными, приведенными в табл.4.2. 10. По результатам опытов построить зависимость νпоп = f(hg, B) или φy = f(hg).
Табл. 4.1
Табл. 4.2
По результатам измерений строим график зависимости ν поп, φy от hg
Лабораторная работа № 5
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.79.193 (0.01 с.) |

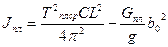 ,
,
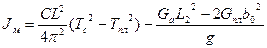 , (13)
, (13)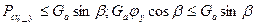 (14)
(14)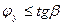
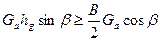 (15)
(15)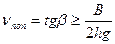 , где β - угол поперечного наклона опорной поверхности; hg– высота центра тяжести модели; ν поп - коэффициент поперечной устойчивости.
, где β - угол поперечного наклона опорной поверхности; hg– высота центра тяжести модели; ν поп - коэффициент поперечной устойчивости.