
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексная математическая модель всеазимутальной РНСодержание книги
Поиск на нашем сайте
Комплексность математической модели обусловлена следующими причинами. 1. На ранних этапах работы при наличии большого количества альтернатив объем информации об исследуемом объекте минимален и ограничен его внешними обводами, параметрами завязки конструкции (стартовой тяговооруженностью, нагрузкой на крыло, типом ДУ) и начальным приближением программ управления. На основе этих исходных данных необходимо определить аэродинамические и массово-центровочные характеристики исследуемого ЛА, например КРБ, его тепловые режимы и параметры ДУ, и только затем приступить к моделированию полета и анализу полученных результатов. 2. Взаимосвязь частных математических моделей базируется на общности используемых исходных данных. Например, внешние обводы служат основой для расчета аэродинамических характеристик, массово-центровочной сводки и тепловых режимов КРБ, а данные по аэродинамике, массовым параметрам и характеристикам ДУ, в свою очередь, используются динамической моделью для расчета вектора равнодействующей внешних сил при моделировании движения центра масс. 3. Выводы и рекомендации, выработанные на этапе баллистического проектирования, не должны существенным образом изменяться на более поздних этапах проектирования и конструирования. Это делает невозможным проведение "чистой" оптимизации отдельных структурных или функциональных элементов, например, программ управления КРБ, без оценки того, насколько полученные программы согласуются с существующей аэродинамикой или отведенными лимитами массы конструкции системы спасения; компонуется ли КРБ при имеющихся внешних обводах с РН, стартовым устройством и пр. Процесс построения комплексной математической модели включает в себя: -формальное описание объекта исследований, полнота которого зависит от требований к точности прогнозирования его характеристик; -установление функциональной связи между независимыми (фиксированными для исследуемого варианта ЛА) и зависимыми параметрами; -математическое описание объекта исследований с помощью систем уравнений, т.е. создание его статической и динамической моделей; -программную реализацию комплексной математической модели. Рассмотрим комплексную математическую модель всеазимутальной РН, используемую на этапах согласования и оптимизации проектно-баллистических параметров и управления. Комплексная модель включает в себя модель движения (динамическую модель), модели двигательной установки, комплекса автономного управления (КАУ), аэродинамическую модель, а также методики расчета тепловых режимов КРБ, массовых сводок систем и агрегатов одноразовой ступени и системы спасения КРБ. Динамическая модель Основой комплексной математической модели всеазимутальной РН является динамическая модель, описывающая движение РН и ее составных элементов: ракетных блоков и отделяющихся частей на различных этапах полета и объединяющая результаты расчетов, которые выполняются в рамках других моделей. С точки зрения динамики полета наибольший интерес представляет КРБ, сочетающий «ракетную» схему выведения в составе РН, а также управляемый, «по-самолетному», планирующий полёт на участке манёвра возврата и «моторный» (с помощью вспомогательной воздушнореактивной двигательной установки) крейсерский полёт в атмосфере на дозвуковой скорости. Причем, если участок крейсерского полета по режимам движения и нагружению конструкции идентичен полету дозвукового неманевренного самолета, то участок маневра возврата имеет существенные отличия как от участка спуска орбитального самолета, так и от режимов движения обычных самолетов. На этапе баллистического проектирования при исследовании вопросов динамики полета основное внимание уделяется анализу уравнений движения центра масс. При этом, в связи с трудностью получения в процессе синтеза облика ЛА значений демпфирующих аэродинамических моментов, собственных моментов инерции, определяемых по результатам углубленной проработки проекта и экспериментальных исследований, динамические уравнения движения ЛА относительно центра масс заменяются статическими уравнениями моментов внешних сил, предусматривающих взаимную компенсацию на заданном угле атаки моментов относительно центра масс от аэродинамической силы и силы тяги ДУ, отклонённой на соответствующий балансировочный угол. Общий вид уравнений движения определяется выбором системы координат, в проекции на оси которой они записываются, а также полнотой учета сил и моментов, действующих на КРБ в полете и при движении по взлётно-посадочной полосе (ВПП) при посадке. В этой системе координат (рис.1) положение центра масс определяется сферическими координатами: радиусом-вектором, а также геоцентрической широтой и долготой r, Система дифференциальных уравнений, описывающих движение центра масс КРБ в сферически-скоростной системе координат, связанной с вращающейся Землей, имеет следующий вид:
где проекции векторов кориолисовой
где проекции векторов кориолисовой
и
При этом в отличие от традиционного варианта записи системы уравнений движения в сферически-скоростной системе координат, приведенная система уравнений адаптирована к решению задач моделирования маневра возврата и крейсерского полета КРБ, длительное время летящего с дозвуковой скоростью, путем учета меридиональной
Рис.1 Сферически-скоростная система координат
В качестве исходных данных при анализе влияния ветровых составляющих на изменение параметров траектории используется зимнее высотное распределение профиля ветра для района космодрома Плесецк, приведенное на рис.2. Следует также обратить внимание на то, что орты При моделировании пространственного движения ЛА будем считать, что вектор равнодействующей внешних сил -силу притяжения Земли, -равнодействующую вектора аэродинамических сил, -равнодействующую силы тяги ДУ, Определим проекции этих сил на оси сферически-скоростной системы координат. Сила притяжения
где u – гравитационный потенциал Земли. В общем виде гравитационный потенциал Земли представляется в помощью бесконечного ряда, однако в процессе моделирования траектории полета РН при соблюдении приемлемой точности достаточно в разложении ограничиться тремя первыми членами, являющимися сферическими функциями нулевого, второго и четвертого порядков.
где Оценим относительные величины кориолисова
Рис.2 Высотный профиль ветра
Расчеты показывают, что максимальные относительные величины:
С учетом этого определим составляющие ускорения силы притяжения в сферической системе координат
Воспользовавшись матрицей направляющих косинусов между сферической и скоростной системами координат, получаем
Найдем теперь составляющие равнодействующей вектора аэродинамических сил -силы лобового сопротивления X; -подъемной силы Y; -боковой силы Z. При моделировании полета ЛА в атмосфере примем ряд допущений: -система управления обеспечивает ориентацию вектора скорости в плоскости тангажа; -угловые скорости по углам атаки и крена малы, вследствие чего перекрестные аэродинамические связи между каналами тангажа, рыскания и крена отсутствуют; -координаты центра масс и центра давления лежат в плоскости тангажа.
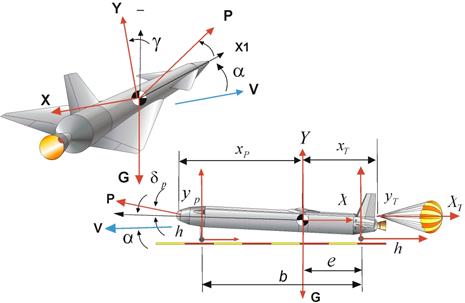
Рис.3 Схема сил, действующих на КРБ в полёте и при движении по ВПП
Перечисленные допущения позволяют при моделировании пространственного движения ЛА в атмосфере избежать учета его аэродинамических характеристик по углу скольжения и за счет этого сократить в два раза необходимый объем аэродинамических данных для ЛА типа крылатых ракетных блоков, не обладающих в отличие от обычных РН аэродинамической симметрией по углам Нецелесообразность использования программы управления по рысканию на атмосферном участке полета обуславливается также и чисто аэродинамическими причинами. Например, на участке маневра возврата КРБ, появление даже небольшого скольжения на умеренных углах атаки, нарушает симметрию вихревой системы вокруг корпуса КРБ, вследствие чего возникает значительная нестационарная боковая сила, вызывающая тряску КРБ и ухудшающая его путевую устойчивость и управляемость. Спроектировав силу лобового сопротивления и подъемную силу на оси скоростной системы координат, получаем
где q – скоростной напор;
Для вычисления характерной площади у крылатых ЛА обычно используют площадь крыла или квадрат размаха крыла. Однако на этапе оптимизации проектно-баллистических параметров КРБ, когда характеристики аэродинамических поверхностей изменяются в процессе расчетов, в качестве характерной площади Определим теперь проекции равнодействующей силы тяги двигательной установки - при управлении на атмосферном участке полета
- при управлении на безатмосферном участке полета
где Наконец, последней составляющей вектора -сила тяжести -суммарная аэродинамическая сила -сила тяги ДУ -реакция поверхности ВПП на стойки шасси -сила трения качения пневматиков шасси Нагрузки на носовую и главные стойки шасси (
Последнее из уравнений представляет собой условие равенства моментов внешних сил относительно центра масс ЛА, где Сделав допущение о том, что поверхность ВПП плоская и не имеет уклона, при моделировании движения ЛА в процессе разбега или пробега, систему уравнений (3.1) можно заменить упрощенной системой, состоящей из двух дифференциальных уравнений
Далее рассмотрим вопросы разработки методик расчета массово-центровочных характеристик РН и КРБ, составляющих внешних сил (аэродинамики и тяги двигательной установки), оценки тепловых режимов, а также создания базы данных аэродинамических характеристик ЛА.
|
||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.009 с.) |

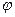 ,
, 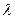 ,связанными с базовой прямоугольной системой координат, а его вектор скорости
,связанными с базовой прямоугольной системой координат, а его вектор скорости 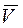 - модулем скорости V, углом наклона к плоскости местного горизонта
- модулем скорости V, углом наклона к плоскости местного горизонта 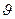 и курсовым углом
и курсовым углом 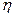 , т.е. углом между местной параллелью и проекцией вектора скорости на плоскость местного горизонта. Причем векторы ускорения и равнодействующей внешних сил проектируются на направления касательной к траектории, нормали, лежащей в плоскости векторов
, т.е. углом между местной параллелью и проекцией вектора скорости на плоскость местного горизонта. Причем векторы ускорения и равнодействующей внешних сил проектируются на направления касательной к траектории, нормали, лежащей в плоскости векторов 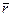 и
и 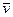 , и нормали к этой плоскости.
, и нормали к этой плоскости.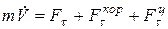 ;
;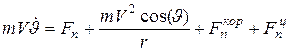 ; (1)
; (1)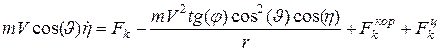 ;
;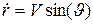 ;
;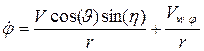 ;
;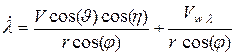 ,
,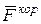 и переносной сил
и переносной сил 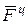 вычисляются с помощью уравнений
вычисляются с помощью уравнений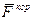 и переносной сил
и переносной сил 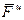 вычисляются с помощью уравнений (2) и (3).
вычисляются с помощью уравнений (2) и (3).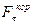 =0;
=0;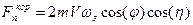 ; (2)
; (2)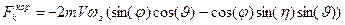 ;
;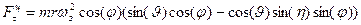 ;
;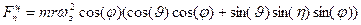 ; (3)
; (3)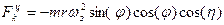 .
.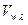 и широтной
и широтной  ветровых составляющих.
ветровых составляющих.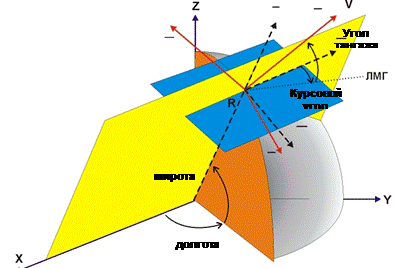
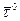 ,
, 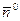 ,
, 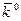 образуют левую тройку векторов. Такая ориентация была выбрана с целью согласования параметров
образуют левую тройку векторов. Такая ориентация была выбрана с целью согласования параметров 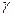 ,
, 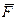 (рис.3) включает в себя:
(рис.3) включает в себя: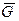 ;
;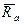 ;
;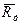 .
.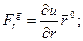
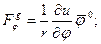
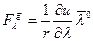 , (4)
, (4)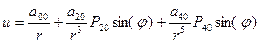 , (5)
, (5)
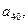 - константы, а
- константы, а 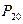 ,
, 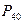 - полиномы Лежандра второго и четвертого порядка, определяемые по формулам
- полиномы Лежандра второго и четвертого порядка, определяемые по формулам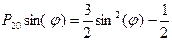 ;
;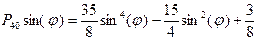 . (6)
. (6)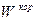 и центробежного
и центробежного 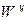 ускорений, а также вклад двух последних членов в формуле (5). Для этого рассмотрим две точки на траектории полета РН, стартующей с широты 45 град, которые соответствуют моментам отделения КРБ первой ступени (
ускорений, а также вклад двух последних членов в формуле (5). Для этого рассмотрим две точки на траектории полета РН, стартующей с широты 45 град, которые соответствуют моментам отделения КРБ первой ступени (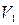 =1800 м/с,
=1800 м/с, 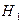 =53 км,
=53 км, 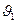 =23 град) и сбросу головного обтекателя в антиподную точку (
=23 град) и сбросу головного обтекателя в антиподную точку (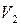 =7520 м/с,
=7520 м/с, 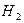 =115 км,
=115 км, 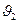 =0.7 град).
=0.7 град).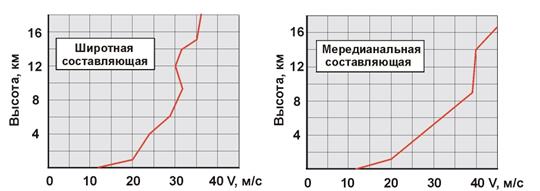
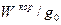 ,
, 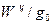 ,
, 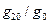 ,
, 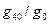 не превосходят соответственно значений: 2.56, 2.45, 0.08 и 0.00046 % - в первом случае и 10.75, 2.47, 0.079 и 0.00044% - во втором. Поэтому на этапе баллистического проектирования с достаточной степенью точности нормальный потенциал Земли можно заменить следующим приближенным выражением
не превосходят соответственно значений: 2.56, 2.45, 0.08 и 0.00046 % - в первом случае и 10.75, 2.47, 0.079 и 0.00044% - во втором. Поэтому на этапе баллистического проектирования с достаточной степенью точности нормальный потенциал Земли можно заменить следующим приближенным выражением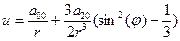 . (7)
. (7)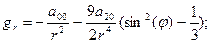
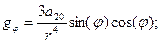 (8)
(8)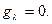
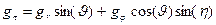 ;
;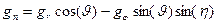 ; (9)
; (9)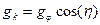 .
.
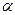 и
и 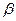 .
.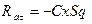 ;
;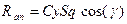 ; (10)
; (10)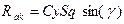 ,
,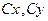 - коэффициенты силы лобового сопротивления и подъемной силы, отнесенные к характерной площади;
- коэффициенты силы лобового сопротивления и подъемной силы, отнесенные к характерной площади;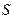 удобно пользоваться площадью миделя его корпуса, являющейся, как это вытекает из постановочной части задачи (предусматривающей у КРБ наличие одноразового прототипа), величиной постоянной.
удобно пользоваться площадью миделя его корпуса, являющейся, как это вытекает из постановочной части задачи (предусматривающей у КРБ наличие одноразового прототипа), величиной постоянной.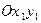 связанной системы координат на угол
связанной системы координат на угол 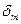 , а на безатмосферном участке траектории, с целью обеспечения пространственного выведения, дополнительно на угол
, а на безатмосферном участке траектории, с целью обеспечения пространственного выведения, дополнительно на угол 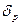 в плоскости
в плоскости 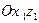 имеем
имеем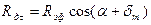 ;
;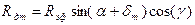 ; (11)
; (11)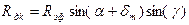 ,
,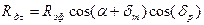 ;
;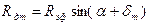 ; (12)
; (12)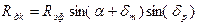 ,
,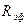 - эффективная тяга ДУ, определяемая как разность между идеальной тягой двигателя (
- эффективная тяга ДУ, определяемая как разность между идеальной тягой двигателя (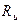 ) и потерями (
) и потерями (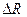 ), обусловленными установкой двигателя на конкретный вариант ЛА, нерасчетными режимами работы ДУ и пр.
), обусловленными установкой двигателя на конкретный вариант ЛА, нерасчетными режимами работы ДУ и пр.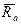 ;
;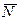 ;
;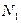 и
и 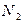 ) определяются путем решения системы линейных уравнений
) определяются путем решения системы линейных уравнений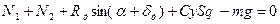 ;
;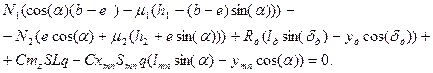 (13)
(13)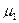 ,
, 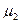 - коэффициенты трения качения (для сухого бетонного покрытия и незаторможенных колес:
- коэффициенты трения качения (для сухого бетонного покрытия и незаторможенных колес: 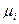 =0.04, для заторможенных:
=0.04, для заторможенных: 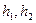 - расстояние от поверхности ВПП до продольной оси ЛА при обжатых амортизаторах;
- расстояние от поверхности ВПП до продольной оси ЛА при обжатых амортизаторах;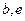 – база и вынос колес главных стоек шасси относительно центра масс;
– база и вынос колес главных стоек шасси относительно центра масс;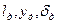 - координаты ДУ и угол ориентации вектора тяги относительно продольной оси ЛА;
- координаты ДУ и угол ориентации вектора тяги относительно продольной оси ЛА;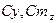 - коэффициент подъемной силы и коэффициент момента тангажа относительно центра масс ЛА;
- коэффициент подъемной силы и коэффициент момента тангажа относительно центра масс ЛА;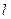 - характерная длина ЛА;
- характерная длина ЛА;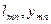 - координаты узла крепления тормозного парашюта в БСК;
- координаты узла крепления тормозного парашюта в БСК;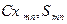 - коэффициент силы лобового сопротивления и площадь тормозного парашюта;
- коэффициент силы лобового сопротивления и площадь тормозного парашюта;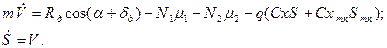 (14)
(14)


