Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметр поврежденности Работнова-КачановаСодержание книги
Поиск на нашем сайте
Можно построить модель рассеянного хрупкого разрушения, введя новый безразмерный параметр поврежденности. Л.М.Качановым и Ю.Н.Работновым независимо и практически одновременно была предложена простейшая модель накопления повреждений, положившая начало бурно развивающейся области – механике рассеянного разрушения или механике повреждений (damage mechanics). Идея подхода состоит в том, что в материале предполагается рост внутренних дефектов, эквивалентный уменьшению эффективного сечения образца. Например, при одноосном растяжении напряжением σ0 начальное сечение стержня
Далее принимается кинетическая гипотеза о том, что скорость роста параметра поврежденности зависит от эффективного напряжения, и простейшее предположение состоит в степенном характере этой зависимости:
Интегрируя уравнение роста параметра поврежденности (4.2.2) и подставляя начальные условия (
Можно рассмотреть три события, соответствующие трем условиям окончательного разрушения: 1. Всё сечение разрушено:
Критическое время при этом:
2. Сечение уменьшилось пропорционально
Критическое время: Если принять для наглядной оценки 3. Поврежденность достигла некоторого критического значения:
при котором начинается неустойчивый рост дефектов. Последнее предположение наиболее правдоподобно и соответствует достижению критической длины для роста усталостной трещины. Такой же качественный вывод следует из анализа «модели пучка волокон» (разд. 4.2.3), когда накопление дискретных разрывов волокон, задолго до разрушения всех волокон, приводит к возникновению неустойчивого процесса последовательного разрыва волокон без роста (при уменьшении) внешней нагрузки, что соответствует возникновению «падающего» участка на диаграмме деформирования. Эксперименты по нагружению углепластиков с разной скоростью деформации показывают, что критическое значение параметра поврежденности
Если принять В более общем случае кинетическое уравнение (4.2.2)
Полагая в начальный момент σ0=σ е при t =0 и в момент разрушения:
совпадающее с (4.2.5) при степенном виде (4.2.2) функции В данном разделе приведены упрощенные соотношения механики накопления повреждений - с единственной целью - отметить, что введение параметра (вектора, тензора) поврежденности и кинетического уравнения его роста типа (4.2.2), (4.2.11) позволяет из экспериментов при простых режимах нагружения определять параметры материала (С и n) и оценивать долговечность при других режимах нагружения. Прочность пучка волокон Эта модель отражает влияние статистического разброса прочности волокон на реализацию их прочности в однонаправленном композите. Этот «третий секрет прочности» подробно обсужден в Лекции 1.2. Для исследования влияния разброса прочности по результатам испытаний на разрыв большого числа волокон строят гистограмму – ступенчатую фигуру (рис. 2.4.1, а), в которой высота каждой ступени зависит от числа волокон с прочностью в границах данной ступени Если приложенное напряжение достаточно велико
который называется функцией распределения
Рис. 4.2.1. Функции распределения – б и плотности распределения – а прочности волокон Модель разрушения пучка Предположим, что в пучке N несвязанных волокон. С ростом приложенного среднего напряжения σ0 разрушилось n (σ0) наиболее «слабых» волокон. Значит, нагрузка распределилась на оставшиеся
На рис. 4.2.2 показана условная зависимость начального напряжения
Рис. 4.2.2. Иллюстрация понятия прочности пучка волокон
Из условия максимума (4.2.13):
и прочность пучка
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

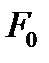 с ростом параметра поврежденности ω уменьшается и становится равным:
с ростом параметра поврежденности ω уменьшается и становится равным: 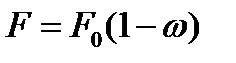 . При этом эффективное напряжение при постоянной нагрузке растет
. При этом эффективное напряжение при постоянной нагрузке растет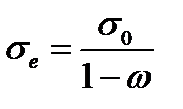 . (4.2.1)
. (4.2.1)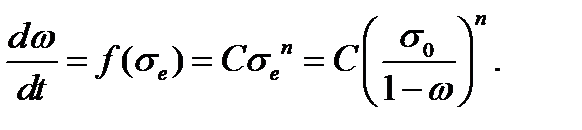 (4.2.2)
(4.2.2)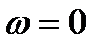 при
при 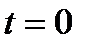 ), получим
), получим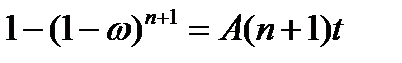 , где
, где 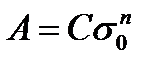 . (4.2.3)
. (4.2.3)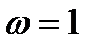 . (4.2.4)
. (4.2.4)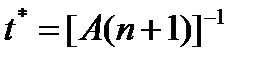 . (4.2.5)
. (4.2.5)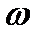 , и напряжение
, и напряжение 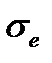 (4.2.1) в расчете на ослабленное сечение
(4.2.1) в расчете на ослабленное сечение 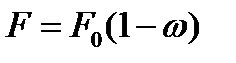 достигло предела прочности
достигло предела прочности 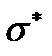 :
: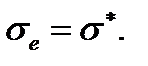 (4.2.6)
(4.2.6)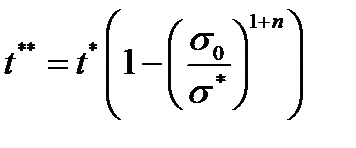 . (4.2.7)
. (4.2.7)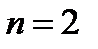 , а приложенное напряжение
, а приложенное напряжение 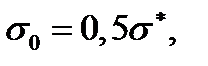 то поправка (4.2.7) по отношению к (4.2.5) составит 12%. При экспериментальной оценке разброс по долговечности на разных образцах достигает 100 %, поэтому уточнения на проценты несущественны, и часто пользуются простейшим условием (4.2.4).
то поправка (4.2.7) по отношению к (4.2.5) составит 12%. При экспериментальной оценке разброс по долговечности на разных образцах достигает 100 %, поэтому уточнения на проценты несущественны, и часто пользуются простейшим условием (4.2.4).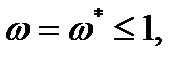 (4.2.8)
(4.2.8)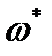 не является константой материала, но это значение при разрушении равно 0,5…0,7, т.е. существенно меньше единицы. Критическое время для условия 3:
не является константой материала, но это значение при разрушении равно 0,5…0,7, т.е. существенно меньше единицы. Критическое время для условия 3: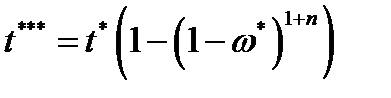 . (4.2.9)
. (4.2.9)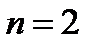 ,
, 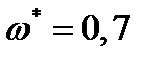 , то поправка (4.2.9) по сравнению с
, то поправка (4.2.9) по сравнению с 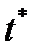 из (4.2.5) составит всего 3%. После достижения критической поврежденности
из (4.2.5) составит всего 3%. После достижения критической поврежденности 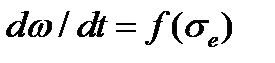 допускает следующее решение. Из определения эффективного напряжения (4.2.1):
допускает следующее решение. Из определения эффективного напряжения (4.2.1): 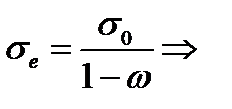
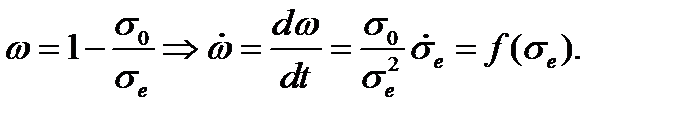 (4.2.10)
(4.2.10)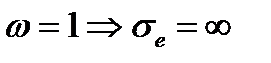 при t = t *, находим критическое время до разрушения:
при t = t *, находим критическое время до разрушения: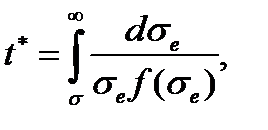 (4.2.11)
(4.2.11)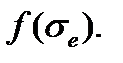
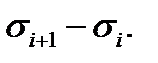 Затем гистограмму нормируют, относя число волокон в каждом прямоугольнике гистограммы к общему числу испытанных волокон N и к шагу гистограммы
Затем гистограмму нормируют, относя число волокон в каждом прямоугольнике гистограммы к общему числу испытанных волокон N и к шагу гистограммы 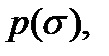 которая определена от некоторого наименьшего
которая определена от некоторого наименьшего 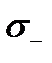 значения прочности до наибольшего
значения прочности до наибольшего 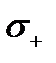 .
.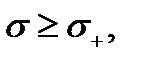 разрушение обязательно произойдёт, его вероятность равна единице. При малых напряжениях
разрушение обязательно произойдёт, его вероятность равна единице. При малых напряжениях 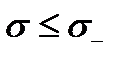 разрушение не происходит, его вероятность равна нулю. При промежуточном напряжении
разрушение не происходит, его вероятность равна нулю. При промежуточном напряжении 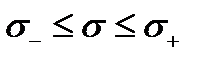 вероятность разрушения равна площади под кривой слева от значения
вероятность разрушения равна площади под кривой слева от значения 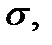 то есть равна интегралу
то есть равна интегралу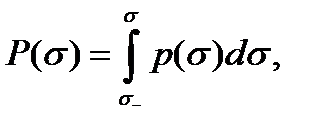 (4.2.12)
(4.2.12)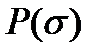 (рис. 4.2.1, б).
(рис. 4.2.1, б).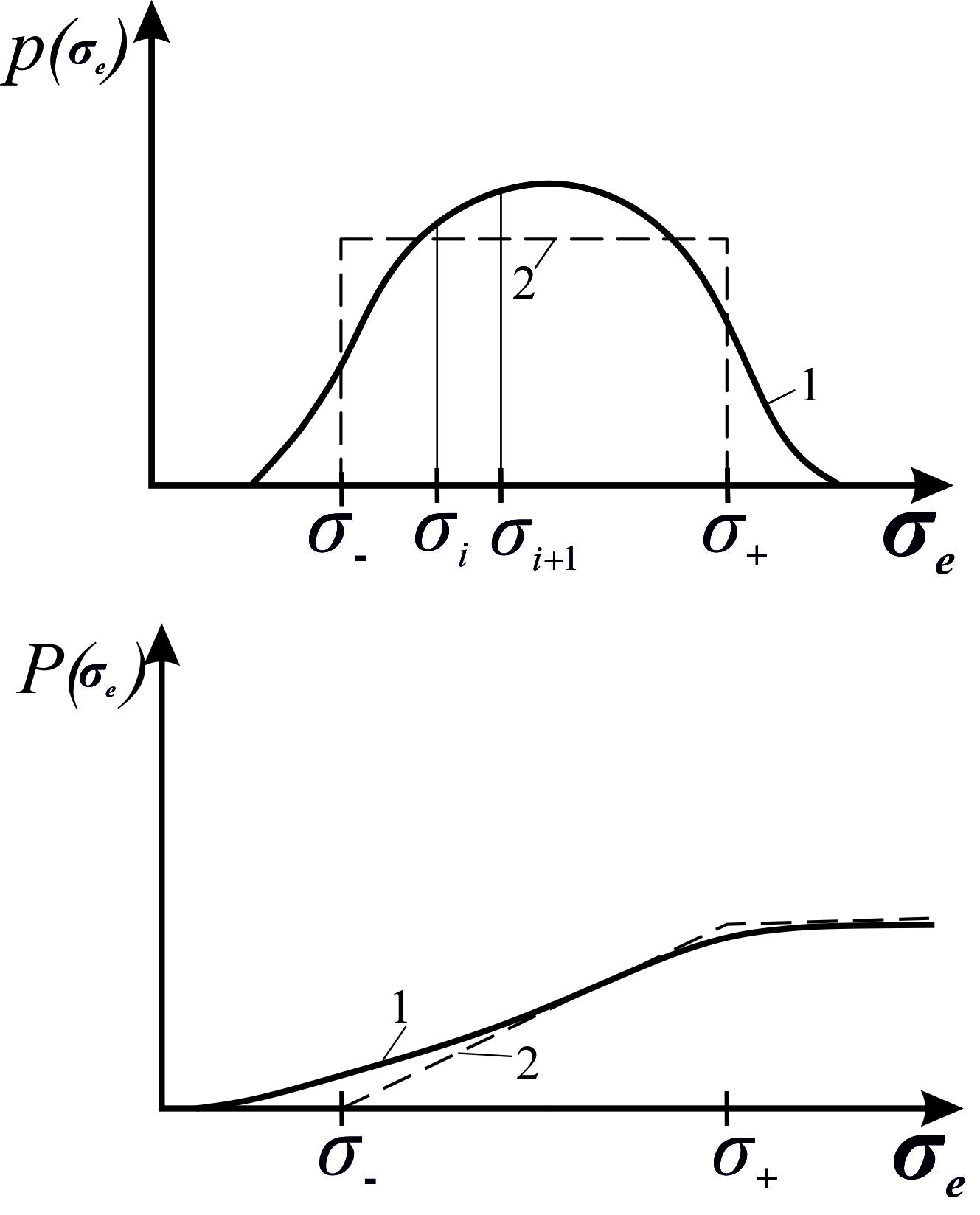
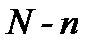 волокон, и истинное напряжение на волокно σ e связано с начальным средним σ0 следующим выражением:
волокон, и истинное напряжение на волокно σ e связано с начальным средним σ0 следующим выражением: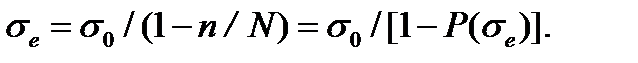
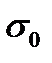 от истинного
от истинного 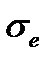 , и максимум этой зависимости соответствует критическому истинному напряжению
, и максимум этой зависимости соответствует критическому истинному напряжению 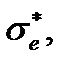 которое можно пересчитать в критическое условное напряжение
которое можно пересчитать в критическое условное напряжение 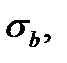 называемое «прочность пучка».
называемое «прочность пучка».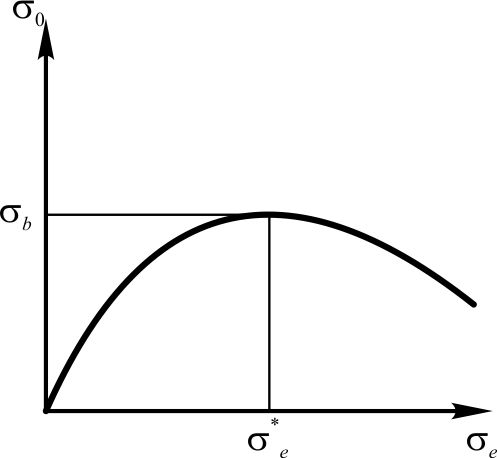
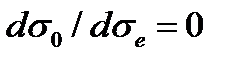 получаем уравнение, определяющее критическое напряжение
получаем уравнение, определяющее критическое напряжение 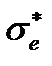 :
: