
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие указания к решению задачСодержание книги Поиск на нашем сайте
Предлагаемые методические рекомендации содержат задачи из двух разделов общего курса физики в соответствии с учебными программами курса, читаемого на кафедре «Физика», «Механика» и «Молекулярная физика и термодинамика». Данное издание предназначено для самостоятельной работы студентов и проведения практических занятий. Решения задач следует начинать с краткой записи условия с приведением его к СИ. Значения физических величин и постоянных представлены в таблицах А.1–А.14. Решения необходимо сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда это возможно, дать чертеж, выполненный с помощью чертежных принадлежностей. Решать задачу надо в общем виде, т. е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин. После получения расчетной формулы для проверки ее правильности следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно. Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени. При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 3,52 · 103, вместо 0,00129 записать 1,29 · 10–3 и т. п. Вычисления по расчетной формуле необходимо проводить с соблюдением правил приближенных вычислений [6]. Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора. Физические основы механики
Основные формулы Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x: x = f (t), где x – некоторая функция времени t. Проекция средней скорости на ось x
Средняя путевая скорость
где Δ s – путь, пройденный точкой за интервал времени Δ t. Путь Δ s в отличие от разности координат Δ x = x 2 – x 1 не может убывать и принимать отрицательные значения, т. е. Δ s
Проекция среднего ускорения на ось x
Проекция мгновенного ускорения на ось x
Кинематическое уравнение движения материальной точки по окружности φ = f(t) (r = R = const),
где φ – угловое перемещение. Модуль угловой скорости
Модуль углового ускорения
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
V = ω · R; a τ = ε · R; a n = ω 2 · R,
где V – модуль линейной скорости; a τ и a n – модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε– модуль углового ускорения; R – радиус окружности. Модуль полного ускорения
Угол между полным
α = arccos(a n / a).
Импульс материальной точки массой m, движущейся со скоростью
Второй закон Ньютона
где Силы, рассматриваемые в механике: – сила упругости
где k – коэффициент упругости (в случае пружины – жесткость); D – сила гравитационного взаимодействия
F = γ где γ – гравитационная постоянная; m 1 и m 2 – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки); – сила тяжести
где g – ускорение свободного падения. В случае гравитационного притяжения тела к Земле
где М и R – масса и радиус Земли соответственно; – сила трения (скольжения) F = μ · N,
где μ – коэффициент трения; N – сила нормального давления. Закон сохранения импульса
для двух тел (i = 2)
где Кинетическая энергия тела, движущегося поступательно,
T = m · V 2 / 2
или T = p 2 / 2 m.
Потенциальная энергия: – упругодеформированной пружины
П = k · x 2 / 2,
где k – жесткость пружины; x – абсолютная деформация; – гравитационного взаимодействия
где γ – гравитационная постоянная; m 1 и m 2 – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки); – тела, находящегося в однородном поле силы тяжести,
П = m · g · h,
где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h << R, здесь R – радиус Земли). Закон сохранения механической энергии
E = T + П = const.
Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
А =
Основное уравнение динамики вращательного движения относительно неподвижной оси z
где
J z – момент инерции относительно оси вращения. Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс: – стержня длиной L относительно оси, перпендикулярной стержню,
– обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),
J z = m · R 2,
где R – радиус обруча (цилиндра); – диска радиусом R относительно оси, перпендикулярной плоскости диска,
Проекция на ось z момента импульса тел, вращающихся относительно неподвижной оси z,
L z = J · ω,
где ω – угловая скорость тела. Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z,
J z ·
где J z – момент инерции системы тел относительно оси z;
Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
или T = L z2 / (2 J z).
Релятивистское (лоренцево) сокращение длины стержня
где l 0 – длина стержня в системе, относительно которой стержень покоится (собственная длина); l – длина стержня, относительно которой он движется; β – скорость частицы, выраженная в долях скорости света, β = V / c. Промежуток времени ∆ t в системе, движущейся по отношению к наблюдателю, связан с промежутком времени ∆ t 0 в неподвижной для наблюдателя системе отношением
Релятивистская масса
где m0 – масса покоя. Релятивистский импульс
Полная энергия релятивистской частицы
где Т – кинетическая энергия частицы; Е 0 – энергия покоя частицы, Связь полной энергии с импульсом релятивистской частицы
Связь кинетической энергии с импульсом релятивистской частицы
Типовые задачи
|
||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.231 (0.007 с.) |

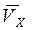 =
= 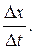
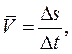
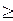 0. Тогда проекция мгновенной скорости на ось x
0. Тогда проекция мгновенной скорости на ось x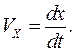
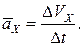

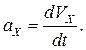
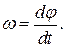
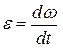 .
.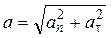 или
или 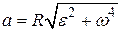 .
.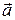 и нормальным
и нормальным 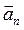 ускорениями
ускорениями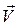 ,
,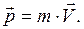
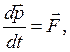
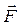 – результирующая сила, действующая на материальную точку.
– результирующая сила, действующая на материальную точку.
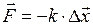 ,
,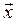 – абсолютная деформация;
– абсолютная деформация;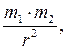
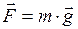 ,
,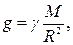
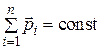 ,
,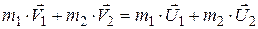 ,
,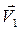 и
и 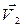 – скорости тел в момент времени, принятый за начальный;
– скорости тел в момент времени, принятый за начальный;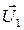 и
и 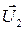 – скорости тех же тел в конечный момент времени.
– скорости тех же тел в конечный момент времени.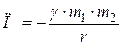 ,
,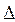 T = T 2 – T 1.
T = T 2 – T 1.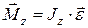 ,
,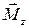 – результирующий момент внешних сил относительно оси z, действующих на тело;
– результирующий момент внешних сил относительно оси z, действующих на тело;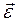 – угловое ускорение;
– угловое ускорение;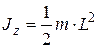 ;
;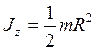 .
.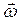 = const,
= const,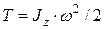
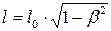 ,
,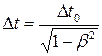 .
.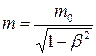 ,
,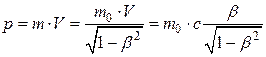 .
.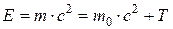 ,
,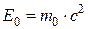 .
.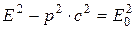 .
.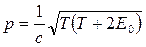 .
.


