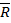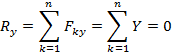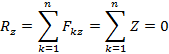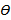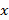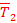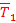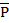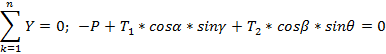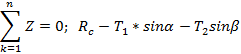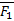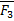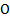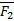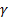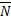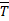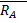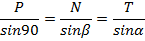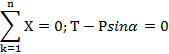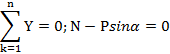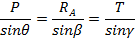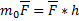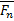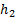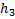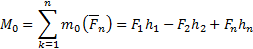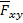Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический и аналитический методы при определении реакции связи, сходящейся системы силСодержание книги
Поиск на нашем сайте
Существует два способа задания и сложения сил: 1) геометрический; 2) аналитический; В первом случае сила задается ка вектор, во втором с помощью проекций на оси координат. Рассмотрим, как складываются силы на примере сходящейся системы сил. Сходящимися называются силы, линии действия которых пересекаются в одной точке. Эти силы могут быть в плоскости и в пространстве.
Геометрический способ В соответствие с четвертой аксиомой, равнодействующая двух пересекающихся сил приложена к точке их пересечения и определяется как диагональ.
Равнодействующая будет также действовать как F1 и F2. На этих силах можно построить силовой треугольник. С помощью теоремы синусов можно найти зависимость сил.
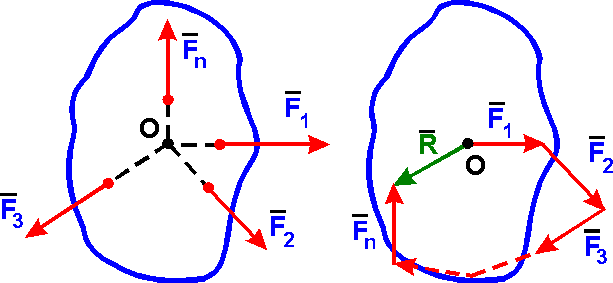
Если имеем систему сходящихся сил, то главный вектор можно определить путём последовательного сложения сил по правилу параллелограмма, но удобнее строить силовой многоугольник.
Система сходящихся сил имеет равнодействующую равную главному вектору этих сил и приложена в точке пересечения.
Из рассуждений очевидно, если силовой многоугольник замкнут, то равнодействующая равна нулю и все силы взаимно уравновешены. Это положение выражает условие равновесия сходящихся сил в геометрической форме.
Для равновесия системы сходящихся сил, приложенных к твердому телу необходимо и достаточно, чтоб равнодействующая равнялась нулю.
Аналитический способ задания и сложения сил.
Силу можно задать с помощью проекции на ось. Проекция вектора
На плоскости:
В пространстве:
Для сложения сил аналитический служит теорема «о проекции вектора суммы»: Проекция вектора суммы на ось равна алгебраической сумме слагаемых сил на ту же ось.
Если рассматривается система сходящихся сил в равновесии, то вектор
Для равновесия любой сходящейся системы сил (на плоскости или в пространстве) необходимо и достаточно, чтоб сумма проекций сил на каждую координатную ось равнялась нулю.
Если силы находятся в одной плоскости, то достаточно двух уравнений.
Составляем уравнение сходящейся пространственной системы сил. Силы уравновешиваются. Для определения Т1, Т2, Rc используем аналитические условия равновесия.
Теорема о трех силах Если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линия этих сил пересекается в одной точке, а силовой треугольник должен быть замкнут.
Так как тело находится в равновесии под действием трех сил, то
Силовой треугольник замкнут.
Действуют три силы: Т, N, Р
Аналитический способ
Пример 2
Решим задачу геометрическим способом
Аналитический метод решения Составим уравнения равновесия в аналитической форме.
При решении задач данного типа применяется принцип освобождаемости от связи, то есть вместо связей указываются их реакции и нагрузки. Если число неизвестных величин больше числа уравнений равновесия, то задача статически неопределима, а система сил называется статически неопределимой.
Момент силы. Моментом силы относительно произвольного центра в плоскости действия силы, называется произведение модуля силы на плечо. Плечо - кратчайшее расстояние от центра О до линии действия силы, но не до точки приложения силы, т.к. сила-скользящий вектор. G AAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAzIlWHygIAACMMQAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54 bWxQSwECLQAUAAYACAAAACEA14V1ItwAAAAHAQAADwAAAAAAAAAAAAAAAACCCgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA8wAAAIsLAAAAAA== ">
Знак момента: По часовой-минус, против часовой-плюс; Момент силы можно выразить как вектор. Это перпендикуляр к плоскости по правилу Буравчика. Если в плоскости расположены несколько сил или система сил, то алгебраическая сумма их моментов даст нам главный момент системы сил.
Рассмотрим момент силы относительно оси, вычислим момент силы относительно оси Z; U ACIYzM62xXwCQKxzcMcCxE3p+KDHsMEYBFBbO5htnsvgarNl25P/AwAA//8DAFBLAwQUAAYACAAA ACEAvcVtuN4AAAAHAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBSE74L/YXkFb3Y3apqS5qWU op6KYCuIt9fkNQnN7obsNkn/vevJHocZZr7J1pNuxcC9a6xBiOYKBJvClo2pEL4Ob49LEM6TKam1 hhGu7GCd399llJZ2NJ887H0lQolxKSHU3neplK6oWZOb245N8E621+SD7CtZ9jSGct3KJ6UWUlNj wkJNHW9rLs77i0Z4H2ncPEevw+582l5/DvHH9y5ixIfZtFmB8Dz5/zD84Qd0yAPT0V5M6USLkCSL kER4ARHcRKlw5IgQx0sFMs/kLX/+CwAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAAT AAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/W AAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAE8ZM7lo CQAA+k0AAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAL3F bbjeAAAABwEAAA8AAAAAAAAAAAAAAAAAwgsAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMA AADNDAAAAAA= ">
Спроецируем F на XY; Fxy=F cosα = ab m0(Fxy)=mz(F), то есть mz=Fxy * h = F cosα * h Момент силы относительно оси равен моменту ее проекции на плоскость перпендикулярную оси, взятому на пересечении осей и плоскости Если сила параллельна оси или пересекает ее, то mz(F)=0
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.90 (0.009 с.) |

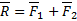
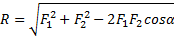

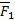
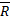
 1
1

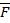 на ось – длина отрезка ab.
на ось – длина отрезка ab.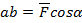
 Например, чтобы определить проекцию силы F на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы Fxy на составляющие по осям координат Fx и Fy.
Например, чтобы определить проекцию силы F на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы Fxy на составляющие по осям координат Fx и Fy.
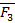

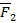
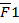

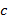
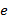
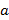


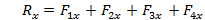
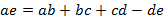
 (1)
(1)