
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярно-кінетичні та оптичні властивостіСодержание книги Поиск на нашем сайте
До молекулярно-кінетичних властивостей дисперсних систем відносять броунівський рух, осмотичний тиск, дифузію та седиментаційно-дифузійну рівновагу. Між молекулярно-кінетичними властивостями дисперсних систем та істинних розчинів відсутні якісні відмінності, проте існують суттєві кількісні відмінності, які спричинені значною різницею між розмірами молекул та іонів в істинних розчинах і частинок дисперсної фази в дисперсних системах. Молекулярно-кінетична теорія може бути застосована до дисперсних систем лише тоді, коли розміри частинок дисперсної фази не перевищують 10-6 м і число частинок достатнє для того, щоб можна було застосувати закони статистики. У рідинах та газах дисперговані колоїдні частинки, як і молекули, перебувають у тепловому русі. Порівняно легкі молекули газів (розміром близько 10-10 м) рухаються зі швидкістю сотні метрів за секунду, в той же час значно важчі колоїдні частинки (розміром 10-9 – 10-7 м) рухаються зі швидкістю кілька міліметрів за секунду, оскільки середня кінетична енергія руху частинки не залежить від її розміру і є сталою за певної температури. У середовищі рідини чи газу колоїдна частинка рухається складною траєкторією, багатократно змінюючи напрям руху внаслідок безперервних зіткнень з молекулами середовища. Так виникає броунівський рух. Теорія броунівського руху в колоїдних системах була розроблена Ейнштейном та Смолуховським. Відповідно до неї броунівський рух характеризується величиною середнього квадратового значення зсуву частки:
де n – кількість узятих для розрахунку середніх проекцій довільного зсуву частки на довільну вісь за певний проміжок часу. Рівняння Ейнштейна‑Смолуховського встановлює залежність величини зсуву частинки за певний час t від в’язкості дисперсійного середовища h, радіуса частинки дисперсної фази r та температури Т:
З рівняння (4.2) видно, що інтенсивність броунівського руху є обернено пропорційною до розмірів часток. Одним із наслідків теплового руху є дифузія. За Ейнштейном величина коефіцієнта дифузії залежить від в’язкості дисперсійного середовища і розмірів часток, що рухаються:
де D ‑ коефіцієнт дифузії, м2/с; T ‑ температура, K. У золів коефіцієнт дифузії значно менший, ніж у істинних розчинів. Аерозолі (дими, тумани) характеризуються великими значеннями коефіцієнта дифузії, оскільки в’язкість повітря є невеликою (для повітря вона дорівнює 2×10-5 Па×с). Коефіцієнт дифузії і середній зсув часток пов’язані рівнянням:
Осмотичний тиск – тиск, який виникає внаслідок різниці концентрацій по обидва боки напівпроникної мембрани. Його величина залежить від кількості частинок в одиниці об’єму системи і не залежить від природи часток, тобто є колігативною властивістю. Для розведених істинних розчинів, що містять високу концентрацію часток, осмотичний тиск сягає великих значень (десятки атмосфер). Його величину розраховують за рівнянням Вант-Гоффа
де с – молярна концентрація; R – газова стала. Оскільки розміри часток в колоїдних системах є досить великими, а масова концентрація золів є низькою і не перевищує 1%, то концентрація частинок в колоїдних системах є дуже малою. Як наслідок, осмотичний тиск в таких системах є настільки малим, що його важко визначити. Для розрахунку осмотичного тиску в ліозолях можна використовувати рівняння Вант-Гоффа, замінюючи молярну концентрацію с частинною концентрацією n (число часток в 1 м3 золю):
де NA – число Авогадро. На завислі в дисперсній системі частки діють дві сили: сила тяжіння, що зумовлює осідання частинки, та сила дифузії, що протидіє силі тяжіння, прагнучи вирівняти концентрації в усіх точках об’єму системи. Коли між цими двома силами встановлюється рівновага, частки дисперсної фази розподіляються за висотою згідно з рівнянням розподілу Больцмана:
де n h – концентрація часток на висоті h (м) від дна посудини, в якій перебуває система, або від поверхні Землі; n 0 – частинна концентрація золю на рівні дна посудини або поверхні Землі; r та r 0 – густини відповідно дисперсної фази та дисперсійного середовища, кг/м3; m – маса частки, кг; g – прискорення сили тяжіння, м/с2; kБ – константа Больцмана. Розподіл часток за висотою визначається седиментаційною стійкістю системи. Мірою седиментаційної стійкості є гіпсометрична висота, тобто така висота, на якій частинна концентрація становить половину частинної концентрації біля поверхні. Для сферичних часток її можна розрахувати за формулою:
Колоїдні системи з розміром часток 10-9 – 10-7 м (золі, стабілізовані емульсії) є седиментаційно стійкими і можуть зберігатися без осадження протягом тривалого часу. Дисперсні системи з розміром часток 10-7 – 10-4 м (суспензії, не стабілізовані емульсії, пил, дим) є седиментаційно нестійкими системами. Для них є характерним процес седиментації – осідання частинок під дією сили тяжіння. Більшість дисперсних систем яскраво забарвлені і здатні поглинати світло. Крім того особливістю колоїдних систем є здатність інтенсивно розсіювати світло, яка обумовлена близькістю розмірів часток до довжини хвиль видимого світла. Релей вивів рівняння для розсіяння світла золем з непровідними частками, радіус яких є меншим за довжину хвилі світла:
де І та І0 – інтенсивність відповідно розсіяного і падаючого світла; n та n0 – показники заломлення відповідно для дисперсної фази і дисперсійного середовища; n – частинна концентрація золю (кількість часток/м3); V – об’єм частки дисперсної фази (м3); l – довжина хвилі світла (м). Рівняння (4.9) застосовують для безбарвних розведених золів з радіусом часток (r або rекв), меншим за 0,1 l. Відношення k = І/І0 називається відносним світлорозсіянням системи. Якщо відома масова концентрація золю с (кг/м3) та радіус сферичних часток r (м), а також густина дисперсної фази r (кг/м3), рівняння Релея має такий вигляд:
З рівняння (4.10) видно, що розсіяння світла дисперсною системою є тим більшим, чим більшими є концентрація дисперсної фази та об’єм часток і чим меншою є довжина хвилі падаючого світла.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.195.30 (0.006 с.) |

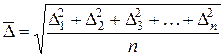 ,
,
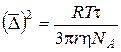 .
.
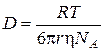 ,
,
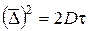 .
.
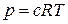 ,
,
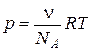 ,
,
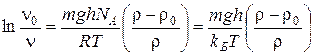 ,
,
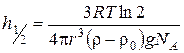 .
.
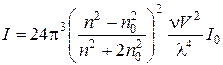 ,
,
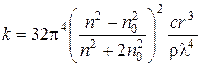 .
.



