Построение кодового дерева Хаффмена

Для иллюстрации алгоритма Хаффмена рассмотрим графический способ построения дерева кодирования. Перед этим введем некоторые определения, принятые для описания алгоритма Хаффмена с использованием этого способа.

Граф -- совокупность множества узлов и множества дуг, направленных от одного узла к другому.

Дерево -- граф, обладающий следующими свойствами:

· ни в один из узлов не входит более одной дуги;

· только в один узел не входит ни одной дуги (этот узел называется корнем дерева);

· перемещаясь по дугам от корня, можно попасть в любой узел.

Лист дерева -- узел, из которого не выходит ни одной дуги. В паре узлов дерева, соединенных между собой дугой, тот, из которого она выходит, называется родителем, другой же -- ребенком.

Два узла называются братьями, если имеют одного и того же родителя.

Двоичное дерево -- дерево, у которого из всех узлов, кроме листьев, выходит ровно по две дуги.

Дерево кодирования Хаффмена -- двоичное дерево, у которого каждый узел имеет вес, и при этом вес родителя равен суммарному весу его детей.

Алгоритм построения дерева кодирования Хаффмена таков:

1. Буквы входного алфавита образуют список свободных узлов будущего дерева кодирования. Каждый узел в этом списке имеет вес, равный вероятности появления соответствующей буквы в сообщении.

2. Выбираются два свободных узла дерева с наименьшими весами. Если имеется более двух свободных узлов с наименьшими весами, то можно брать любую пару.

3. Создается их родитель с весом, равным их суммарному весу.

4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.

5. Одной дуге, выходящей из узла-родителя, ставится в соответствие бит 1, другой -- 0.

6. Пункты 2, 3, 4, 5 повторяются до тех пор, пока в списке свободных узлов не останется только один узел. Этот узел будет являться корнем дерева. Его вес получается равным единице -- суммарной вероятности всех букв сообщения.

Теперь, двигаясь по кодовому дереву сверху вниз и последовательно выписывая двоичные цифры, соответствующие дугам, можно получить коды букв входного алфавита.

Для примера рассмотрим построение дерева кодирования Хаффмена для приведенного в таблице 1 алфавита из восьми букв.

Таблица 1

Буква z1 z2 z3 z4 z5 z6 z7 z8 Вероятность 0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02

Построение дерева начинаем со списка листьев (см. рис. 1) и выполняем по шагам.

Рис. 1. Список свободных узлов-листьев.

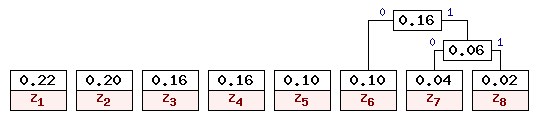
На первом шаге из листьев дерева выбираются два с наименьшими весами z₇ и z₈. Они присоединяются к узлу-родителю, вес которого устанавливается в 0.04 + 0.02 = 0.06. Затем узлы z₇ и z₈ удаляются из списка свободных. Узел z₇ соответствует ветви 0 родителя, узел z₈ -- ветви 1. Дерево кодирования после первого шага приведено на рис. 2.

Рис. 2. Дерево кодирования Хаффмена после первого шага.

На втором шаге "наилегчайшей" парой оказывается лист z₆ и свободный узел (z₇ + z₈). Для них создается родитель с весом 0.16. Узел z₆ соответствует ветви 0 родителя, узел (z₇ + z₈) -- ветви 1. На данном шаге дерево кодирования выглядит следующим образом (см. рис. 3).

Рис. 3. Дерево кодирования Хаффмена после второго шага.

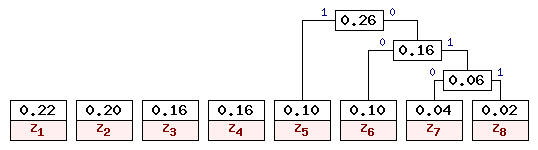
На третьем шаге наименьшие вероятности имеют z₅, z₄, z₃ и свободный узел (z₆ + z₇ + z₈). Таким образом, на данном шаге можно создать родителя для z₅ и (z₆ + z₇ + z₈) с весом 0.26, получив при этом дерево кодирования, представленное на рис. 4. Обратите внимание, что в данной ситуации возможны несколько вариантов соединения узлов с наименьшими весами. При этом все такие варианты будут правильными, хотя и могут привести к различным наборам кодов, которые, впрочем, будут обладать одинаковой эффективностью для заданного распределения вероятностей.

Рис. 4. Дерево кодирования Хаффмена после третьего шага.

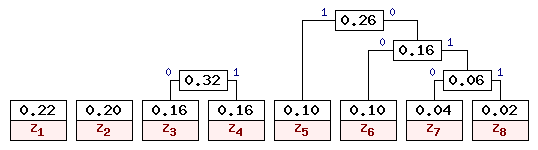
На четвертом шаге "наилегчайшей" парой оказываются листья z₃ и z₄. Дерево кодирования Хаффмена приведено на рис. 5.

Рис. 5. Дерево кодирования Хаффмена после четвертого шага.

На пятом шаге выбираем узлы с наименьшими весами 0.22 и 0.20. Дерево кодирования Хаффмена после пятого шага приведено на рис. 6.

Рис. 6. Дерево кодирования Хаффмена после пятого шага.

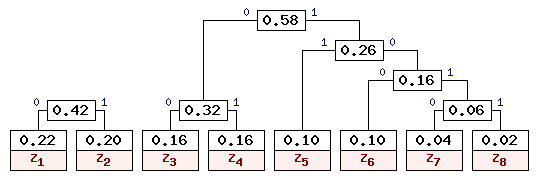
На шестом шаге остается три свободных узла с весами 0.42, 0.32 и 0.26. Выбираем наименьшие веса 0.32 и 0.26. Дерево кодирования Хаффмена после шестого шага приведено на рис. 7.

Рис. 7. Дерево кодирования Хаффмена после шестого шага.

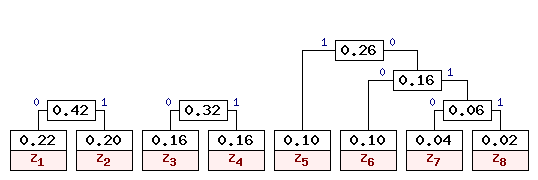
На седьмом шаге остается объединить две оставшиеся свободные вершины, после чего получаем окончательное дерево кодирования Хаффмена, приведенное на рис. 8.

Рис. 8. Окончательное дерево кодирования Хаффмена.

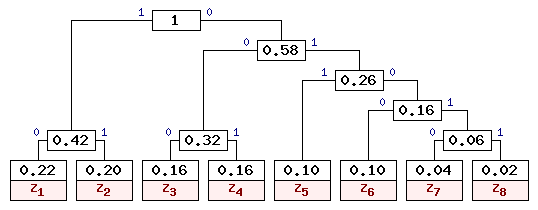
На основании построенного дерева буквы представляются кодами, отражающими путь от корневого узла до листа, соответствующего нужной букве. В рассмотренном примере буквы входного алфавита кодируются так, как показано в таблице 2.

Таблица 2

Буква z1 z2 z3 z4 z5 z6 z7 z8 Код 10 11 000 001 011 0100 01010 01011

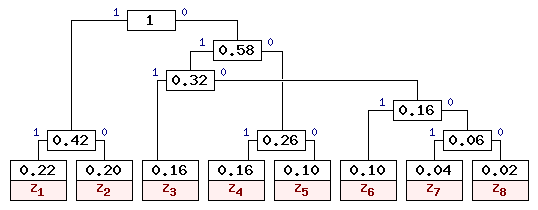
Видно, что наиболее вероятные буквы закодированы самыми короткими кодами, а наиболее редкие -- кодами большей длины. Причем коды построены таким образом, что ни одна кодовая комбинация не совпадает с началом более длинной комбинации. Это позволяет однозначно декодировать сообщения без использования разделительных символов.

Для заданных в таблице 1 вероятностей можно построить и другие правильные варианты кодового дерева Хаффмена. Одно из допустимых деревьев приведено на рис. 9. Коды букв входного алфавита для данного кодового дерева приведены в таблице 3.

Рис. 9. Альтернативный вариант дерева кодирования Хаффмена.

Таблица 3

Буква z1 z2 z3 z4 z5 z6 z7 z8 Код 11 10 011 001 000 0101 01001 01000

Из таблицы 3 видно, что коды также получились префиксными, и наиболее вероятным буквам соответствуют наиболее короткие коды.

Вопросы практической реализации алгоритма

Для повышения эффективности сжатия необходимо, чтобы при построении кодового дерева использовались данные по вероятностям появления букв именно в этом файле, а не усредненные по большому количеству текстов. Исходя из этого, необходима статистика встречаемости букв сжимаемого файла, которая может быть получена предварительным проходом по файлу.

Для ускорения работы принято определять не вероятности появления букв p_i, а частоту встречаемости (количество появлений) буквы в файле n_i. Это позволяет существенно упростить и ускорить алгоритм (не нужно медленных операций с плавающей запятой и операций деления). При таком подходе алгоритм работы не изменяется, так как частоты прямо пропорциональны вероятностям. Стоит заметить, что вес корневого узла дерева кодирования в таком случае будет равен общему количеству букв в обрабатываемом файле.

 

Лекция №7

Автоматизированная система управления или АСУ — комплекс аппаратных и программных средств, предназначенный для управления различными процессами в рамках технологического процесса, производства, предприятия. АСУ применяются в различных отраслях промышленности, энергетике, транспорте и т. п. Термин автоматизированная, в отличие от термина автоматическая подчеркивает сохранение за человеком-оператором некоторых функций, либо наиболее общего, целеполагающего характера, либо не поддающихся автоматизации.

Создателем первых АСУ в СССР является доктор экономических наук, профессор, член-корреспондент Национальной академии наук Беларуси, основоположник научной школы стратегического планирования Николай Иванович Ведута (1913—1998)^[1][2][3][4]. В 1962—1967 гг. в должности директора Центрального научно-исследовательского института технического управления (ЦНИИТУ), являясь также членом коллегии Министерства приборостроения СССР, он руководил внедрением первых в стране автоматизированных систем управления производством на машиностроительных предприятиях. Активно боролся против идеологических PR-акций по внедрению дорогостоящих ЭВМ, вместо создания настоящих АСУ для повышения эффективности управления производством.

Виды АСУ

• Автоматизированная система управления технологическим процессом или АСУ ТП — решает задачи оперативного управления и контроля техническими объектами в промышленности, энергетике, на транспорте

• Автоматизированная система управления производством (АСУ П) — решает задачи организации производства, включая основные производственные процессы, входящую и исходящую логистику. Осуществляет краткосрочное планирование выпуска с учётом производственных мощностей, анализ качества продукции, моделирование производственного процесса. Для решения этих задач применяются MIS и MES-системы, а также LIMS-системы.

Примеры:

o Автоматизированная система управления уличным освещением («АСУ УО») — предназначена для организации автоматизации централизованного управления уличным освещением.

o Автоматизированная система управления наружного освещения («АСУНО») — предназначена для организации автоматизации централизованного управления наружным освещением.

o Автоматизированная система управления дорожным движением или АСУ ДД — предназначена для управления транспортных средств и пешеходных потоков на дорожной сети города или автомагистрали

Автоматизированная система управления предприятием или АСУП — Для решения этих задач применяются MRP,MRP II и ERP-системы. В случае, если предприятием является учебное заведение, применяются системы управления обучением.

SCADA (аббр. от англ. Supervisory Control And Data Acquisition, Диспетчерское управление и сбор данных) — данное понятие обычно применяется к системе управления в промышленности: система контроля и управления процессом с применением ЭВМ. Процесс может быть технологическим, инфраструктурным или обслуживающим:

• Технологические процессы включают — производство, выработку энергии, конструирование, переработка. Может протекать в непрерывном, пакетном, периодическом или дискретном режимах.
• Инфраструктурные процессы могут быть общественными либо частными, и включают: обработку и распределение воды, сбор и обработку сточных вод, нефте- и газо- проводы, передачу и распределение электроэнергии, системы оповещения для гражданской обороны, и большие системы связи.
• Процессы в сфере обслуживания имеют как частную так и общественную стороны — здания, аэропорты, корабли и космические станции. Они контролируют и управляют HVAC, доступом и потреблением энергии.

Основные компоненты системы

SCADA—система обычно содержит следующие подсистемы:

• Человеко-машинный интерфейс (HMI, англ. Human Machine Interface) — инструмент, который представляет данные о ходе процесса человеку оператору, что позволяет оператору контролировать процесс и управлять им.
• Диспетчерская система — собирает данные о процессе и отправляет команды процессору (управление).
• Абонентский оконечный блок, либо УСО (RTU, англ. Remote Terminal Unit), подсоединяемый к датчикам процесса, преобразует сигнал с датчика в цифровой код и отправляет данные в диспетчерскую систему.
• Программируемый Логический Контроллер (PLC, англ. Programmable Logic Controller) используется как полевое устройство из-за экономичности, универсальности и гибкости, нежели RTU специального назначения.
• Коммуникационная инфраструктура для реализации промышленной сети.