Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет чистой текущей стоимости проекта ( NPV )Содержание книги
Поиск на нашем сайте
Цель задачи: ознакомиться с технологиями расчетов текущей стоимости инвестиционных затрат и текущей стоимости доходов за период, сравнительного анализа текущей стоимости инвестиционных затрат и текущей стоимости доходов за период при фиксированных и плавающих ставке дисконтирования и индексе инфляции, реализованными в Excel. Предлагается, пользуясь встроенными функциями Excel: 1) рассчитать текущую стоимость инвестиционных затрат и текущую стоимость доходов за период в 1 год, в 2 года, в 3 года, в 4 года реализации предлагаемого инвестиционного проекта; 2) рассчитать чистую текущую стоимость за период в 1 год, в 2 года, в 3 года, в 4 года реализации предлагаемого инвестиционного проекта; 3) рассчитать чистую текущую стоимость предлагаемого инвестиционного проекта при тех же исходных данных, если ставка дисконтирования – фиксированная и равна 10%, индекс инфляции – фиксированный и равен 10%; 4) рассчитать чистую текущую стоимость предлагаемого инвестиционного проекта при тех же исходных данных, если ставка дисконтирования – фиксированная и равна 10%, индекс инфляции – фиксированный и равен 15%; 5) рассчитать чистую текущую стоимость предлагаемого инвестиционного проекта при тех же исходных данных, если ставка дисконтирования – фиксированная и равна 15%, индекс инфляции – фиксированный и равен 10%; 6) проанализировать полученные результаты. Исходные данные для задания 5 представлены в таблице 1.4: Таблица 1.4
Для расчетов понадобятся следующие функции Excel: · ОКРУГЛ() – для округления результатов вычислений до гривень (3 знак после запятой); · СТЕПЕНЬ() – для нахождения степени числа; · СУММ() – для суммирования по столбцу (строке). ПРИМЕЧАНИЕ: Порядок использования функций – см. в мастере функций, который находится на листе Excel в закладке Вставка в подзакладке Функция (fx). Алгоритм расчетов Рассчитывать текущую стоимость инвестиционных затрат будем по формуле: Для фиксированной ставки дисконтирования рассчитывать текущую стоимость инвестиционных затрат будем по формуле: где Cj – доходы от внедрения проекта по годам; rlk – ставка дисконтирования по годам; n – количество лет, в течение которых производились инвестиции. Рассчитывать текущую стоимость доходов будем по формуле: Для фиксированного индекса инфляции рассчитывать текущую стоимость доходов будем по формуле: где CFi – инвестиции по годам; rk – индекс инфляции по годам; m – количество лет, в течение которых проект будет приносить доходы.
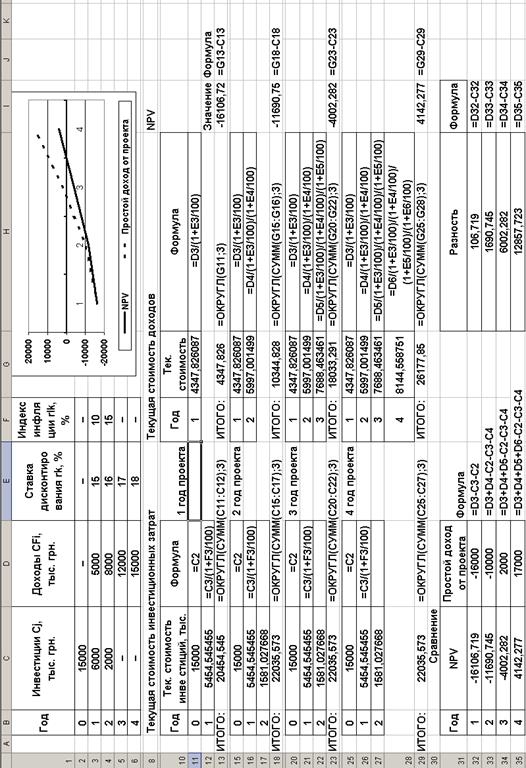
Рассчитывать чистую текущую стоимость будем по формуле: NPV=PV–IC. (13) Рассчитывать чистую текущую стоимость по проекту для переменной ставки дисконтирования и переменного индекса инфляции в Excel по следующему алгоритму (см. рис. 5): 1) рассчитаем текущую стоимость инвестиционных затрат: · за первый год внедрения проекта по формулам в Excel она равна: =ОКРУГЛ(СУММ(C11:C12);3), где C11 – первоначальная сумма инвестиций, которая вычисляется по формуле в Excel следующим образом: =C2; C12 – текущая сумма инвестиций за первый год проекта, которая вычисляется по формуле в Excel следующим образом: =C3/(1+F3/100), где C3 – сумма инвестиций за первый год проекта; F3 – индекс инфляции за первый год проекта. · за второй год внедрения проекта текущая стоимость инвестиционных затрат по формулам в Excel равна: =ОКРУГЛ(СУММ(C15:C17);3), где C15 – первоначальная сумма инвестиций (порядок расчетов см. выше); C16 – текущая сумма инвестиций за первый год проекта (порядок расчетов см. выше); C17 – текущая сумма инвестиций за второй год проекта, которая вычисляется по формуле в Excel следующим образом: =C4/(1+F3/100)/(1+F4/100), где C4 – сумма инвестиций за второй год проекта; F3 – индекс инфляции за первый год проекта; F4 – индекс инфляции за второй год проекта. · поскольку инвестиций по проекту больше нет, то за все последующие годы проекта текущая сумма инвестиций за год проекта равна текущей сумме инвестиций за второй год проекта;
2) рассчитаем текущую стоимость: · за первый год внедрения проекта по формулам в Excel она равна: =ОКРУГЛ(G11;3), где G11 – текущая стоимость доходов за первый год внедрения проекта, которая вычисляется по формуле в Excel следующим образом: =D3/(1+E3/100); где D3 – величина доходов за первый год проекта; Е3 – величина ставки дисконтирования за первый год проекта. · за второй год внедрения проекта текущая стоимость доходов по формулам в Excel равна: =ОКРУГЛ(СУММ(G15:G16);3), где G15 – текущая стоимость доходов за первый год внедрения проекта (порядок расчетов см. выше); G16 – текущая стоимость доходов за второй год проекта, которая вычисляется по формуле в Excel следующим образом: =D4/(1+E3/100)/(1+E4/100), где D4 – величина доходов за второй год проекта; Е3 – величина ставки дисконтирования за первый год проекта; Е4 – величина ставки дисконтирования за второй год проекта; · за третий год внедрения проекта текущая стоимость доходов по формулам в Excel равна: =ОКРУГЛ(СУММ(G20:G22);3), где G20 – текущая стоимость доходов за первый год внедрения проекта (порядок расчетов см. выше); G21 – текущая стоимость доходов за второй год проекта (порядок расчетов см. выше); G22 – текущая стоимость доходов за третий год проекта, которая вычисляется по формуле в Excel следующим образом: =D5/(1+E3/100)/(1+E4/100)/(1+E5/100); где D5 – величина доходов за третий год проекта; Е3 – величина ставки дисконтирования за первый год проекта; Е4 – величина ставки дисконтирования за второй год проекта; Е5 – величина ставки дисконтирования за третий год проекта; · за четвертый год внедрения проекта текущая стоимость доходов по формулам в Excel равна: =ОКРУГЛ(СУММ(G25:G28);3), где G25 – текущая стоимость доходов за первый год внедрения проекта (порядок расчетов см. выше); G26 – текущая стоимость доходов за второй год проекта (порядок расчетов см. выше); G27 – текущая стоимость доходов за третий год проекта (порядок расчетов см. выше); G28 – текущая стоимость доходов за четвертый год проекта, которая вычисляется по формуле в Excel следующим образом: =D6/(1+E3/100)/(1+E4/100)/ (1+E5/100)/(1+E6/100); где D6 – величина доходов за четвертый год проекта; Е3 – величина ставки дисконтирования за первый год проекта; Е4 – величина ставки дисконтирования за второй год проекта; Е5 – величина ставки дисконтирования за третий год проекта; Е6 – величина ставки дисконтирования за четвертый год проекта;
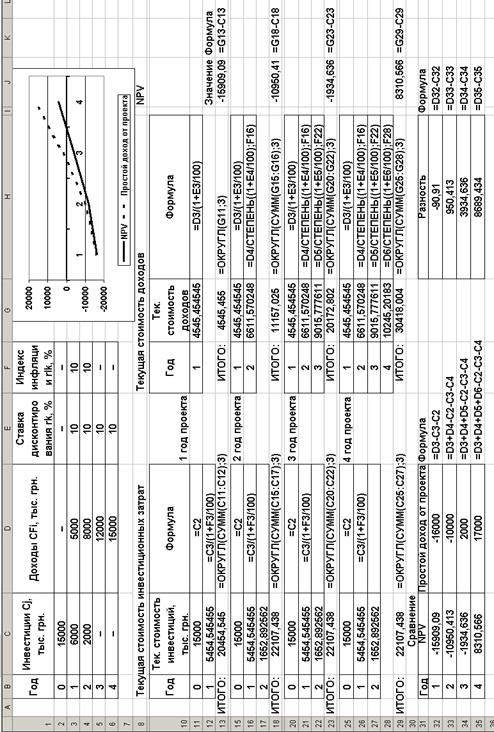
3) рассчитаем чистую текущую стоимость (NPV) по годам: · за первый год внедрения проекта по формулам в Excel она равна: =G13-C13, где G13 – величина текущей стоимости доходов за первый год проекта; C13 – величина текущей стоимости инвестиционных затрат за первый год проекта; · за два года внедрения проекта NPV по формулам в Excel равна: =G18-C18, где G18 – величина текущей стоимости доходов за два года проекта; C18 – величина текущей стоимости инвестиционных затрат за два года проекта; · за три года внедрения проекта NPV по формулам в Excel равна: =G23-C23, где G23 – величина текущей стоимости доходов за три года проекта; C23 – величина текущей стоимости инвестиционных затрат за три года проекта; · за четыре года внедрения проекта NPV по формулам в Excel равна: =G29-C29, где G29 – величина текущей стоимости доходов за четыре года проекта; C29 – величина текущей стоимости инвестиционных затрат за четыре года проекта; На рисунке 5 представлен алгоритм расчетов для переменных ставок и сравнение результатов. Рассчитывать чистую текущую стоимость по проекту для фиксированной ставки дисконтирования и фиксированного индекса инфляции в Excel по следующему алгоритму (см. рис. 6): 1) рассчитаем текущую стоимость инвестиционных затрат: · за первый год внедрения проекта по формулам в Excel она равна: =ОКРУГЛ(СУММ(C11:C12);3), где C11 – первоначальная сумма инвестиций, которая вычисляется по формуле в Excel следующим образом: =C2; C12 – текущая сумма инвестиций за первый год проекта, которая вычисляется по формуле в Excel следующим образом: =C3/(1+F3/100), где C3 – сумма инвестиций за первый год проекта; F3 – индекс инфляции за первый год проекта. · за второй год внедрения проекта текущая стоимость инвестиционных затрат по формулам в Excel равна: =ОКРУГЛ(СУММ(C15:C17);3), где C15 – первоначальная сумма инвестиций (порядок расчетов см. выше); C16 – текущая сумма инвестиций за первый год проекта (порядок расчетов см. выше); C17 – текущая сумма инвестиций за второй год проекта, которая вычисляется по формуле в Excel следующим образом: =C4/СТЕПЕНЬ((1+F4/100);B17), где C4 – сумма инвестиций за второй год проекта; В17 – номер года проекта; F4 – индекс инфляции за второй год проекта. · поскольку инвестиций по проекту больше нет, то за все последующие годы проекта текущая сумма инвестиций за год проекта равна текущей сумме инвестиций за второй год проекта; 2) рассчитаем текущую стоимость: · за первый год внедрения проекта по формулам в Excel она равна: =ОКРУГЛ(G11;3), где G11 – текущая стоимость доходов за первый год внедрения проекта, которая вычисляется по формуле в Excel следующим образом: =D3/(1+E3/100), где D3 – величина доходов за первый год проекта; Е3 – величина ставки дисконтирования за первый год проекта. · за второй год внедрения проекта текущая стоимость доходов по формулам в Excel равна: =ОКРУГЛ(СУММ(G15:G16);3), где G15 – текущая стоимость доходов за первый год внедрения проекта (порядок расчетов см. выше); G16 – текущая стоимость доходов за второй год проекта, которая вычисляется по формуле в Excel следующим образом: =D4/СТЕПЕНЬ((1+E4/100);F16), где D4 – величина доходов за второй год проекта; F16 – номер года проекта; Е4 – величина ставки дисконтирования за второй год проекта; · за третий год внедрения проекта текущая стоимость доходов по формулам в Excel равна:
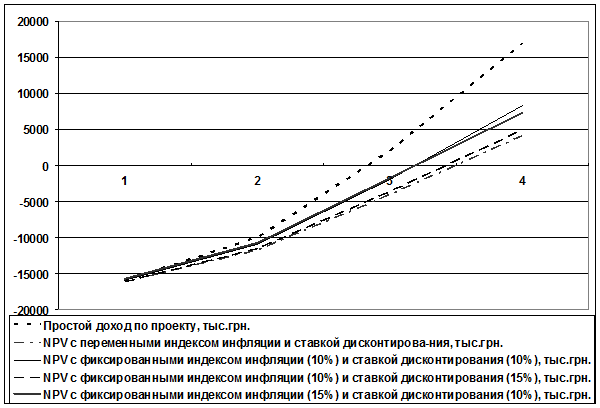
Рис. 5. Алгоритм расчетов по 5 заданию для переменных ставок и сравнение результатов =ОКРУГЛ(СУММ(G20:G22);3), где G20 – текущая стоимость доходов за первый год внедрения проекта (порядок расчетов см. выше); G21 – текущая стоимость доходов за второй год проекта (порядок расчетов см. выше); G22 – текущая стоимость доходов за третий год проекта, которая вычисляется по формуле в Excel следующим образом: =D5/СТЕПЕНЬ((1+E5/100);F22), где D5 – величина доходов за третий год проекта; F22 – номер года проекта; Е5 – величина ставки дисконтирования за третий год проекта; · за четвертый год внедрения проекта текущая стоимость доходов по формулам в Excel равна: =ОКРУГЛ(СУММ(G25:G28);3), где G25 – текущая стоимость доходов за первый год внедрения проекта (порядок расчетов см. выше); G26 – текущая стоимость доходов за второй год проекта (порядок расчетов см. выше); G27 – текущая стоимость доходов за третий год проекта (порядок расчетов см. выше); G28 – текущая стоимость доходов за четвертый год проекта, которая вычисляется по формуле в Excel следующим образом: =D6/СТЕПЕНЬ((1+E6/100);F28), где D6 – величина доходов за четвертый год проекта; F28 – номер года проекта; Е6 – величина ставки дисконтирования за четвертый год проекта; 3) рассчитаем чистую текущую стоимость (NPV) по годам: · за первый год внедрения проекта по формулам в Excel она равна: =G13-C13, где G13 – величина текущей стоимости доходов за первый год проекта; C13 – величина текущей стоимости инвестиционных затрат за первый год проекта; · за два года внедрения проекта NPV по формулам в Excel равна: =G18-C18, где G18 – величина текущей стоимости доходов за два года проекта; C18 – величина текущей стоимости инвестиционных затрат за два года проекта; · за три года внедрения проекта NPV по формулам в Excel равна: =G23-C23, где G23 – величина текущей стоимости доходов за три года проекта; C23 – величина текущей стоимости инвестиционных затрат за три года проекта; · за четыре года внедрения проекта NPV по формулам в Excel равна: =G29-C29, где G29 – величина текущей стоимости доходов за четыре года проекта; C29 – величина текущей стоимости инвестиционных затрат за четыре года проекта; На рисунке 6 представлен алгоритм расчетов для фиксированных ставок (10%) и сравнение результатов: Полученные результаты расчетов представлены в таблице 1.5. Результаты расчетов позволяют сделать следующие выводы: · График NPV с фиксированными индексом инфляции (10%) и ставкой дисконтирования (10%) растет быстрее всего по сравнению с другими графиками NPV. Это объясняется тем, что указанные значения индекса инфляции и ставки дисконтирования – минимальные из представленных вариантов, что и отразилось на конечном значении чистой текущей стоимости проекта при этих исходных данных – 8310,566 тыс. руб.; · При этом сумма простого дохода по проекту больше величины чистой текущей стоимости проекта при этих исходных данных в 2 раза; · График NPV с фиксированными индексом инфляции (15%) и ставкой дисконтирования (10%) занимает второе место по динамике роста. Это объясняется тем, что указанное значение индекса инфляции меньше влияет на результат, что и отразилось на конечном значении чистой текущей стоимости проекта при этих исходных данных – 7365,114 тыс. руб.;
Рис. 6. Алгоритм расчетов по 5 заданию для фиксированных ставок (10%) и сравнение результатов · График NPV с фиксированными индексом инфляции (10%) и ставкой дисконтирования (15%) занимает третье место по динамике роста. Это объясняется тем, что указанное значение ставки дисконтирования больше влияет на результат, чем такое же значение индекса инфляции, что и отразилось на конечном значении чистой текущей стоимости проекта при этих исходных данных – 4953,659 тыс. руб.; · График NPV переменными индексом инфляции и ставкой дисконтирования занимает последнее место по динамике роста. Это объясняется тем, что указанные в таблице 1.4 значения ставки дисконтирования и индекса инфляции существенно снижают эффективность проекта (более чем в 2 раза по сравнению с NPV с фиксированными индексом инфляции (10%) и ставкой дисконтирования (10%)). Это отразилось на конечном значении чистой текущей стоимости проекта при этих исходных данных – 4142,277 тыс. руб.; Таблица 1.5
· На значение чистой текущей стоимости проекта величина индекса инфляции при имеющихся расчетных данных оказывает меньшее влияние (в сторону снижения эффективности проекта), чем величина ставки дисконтирования.
Рис. 7. Графики по исходным значениям, представленным в таблице 1.5 На рис. 7 построены для наглядности графики по исходным значениям, представленным в таблице 1.5.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.204.52 (0.008 с.) |

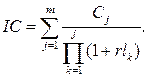 (9)
(9)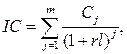 (10)
(10)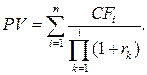 (11)
(11)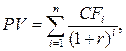 (12)
(12)