Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет линейной регрессии и корреляцииСодержание книги
Поиск на нашем сайте
Цель задачи: ознакомиться с технологиями построения уравнение линейной регрессии, реализации метода наименьших квадратов и расчета линейной корреляции, реализованными в Excel. Предлагается, пользуясь встроенными функциями Excel: 1) построить уравнение линейной регрессии: 2) определить при помощи метода наименьших квадратов величину корреляции между исчисленным расчетным значением y (по построенному уравнению регрессии) и значением y из таблицы 1.1 для 2001-2009 годов. 3) провести анализ полученных результатов. Для расчетов понадобятся следующие функции Excel: · КОРЕНЬ() – для расчета квадратного корня числа; · СУММ() – для суммирования по столбцу (строке); · КОРРЕЛ() – для вычисления парной корреляции. ПРИМЕЧАНИЕ: Порядок использования функций – см. в мастере функций, который находится на листе Excel в закладке Вставка в подзакладке Функция (fx). Исходные данные для задания 2 представлены в таблице 1.1: Таблица 1.1
Алгоритм расчетов Линейная регрессия сводится к определению параметров а0 и а1 уравнения: Система уравнений для определения параметров а0 и а1 выглядит так: где yi и xi – данные таблицы 1; n – количество членов временного ряда. Решение системы (4) находим с помощью метода исключения переменных (вычитая из 1 уравнения системы (4) второе уравнение системы) по следующим формулам: Расчет подготовительных вычислений для системы (4) осуществляем в Excel по формулам: 1) =B5*B5, где В5 – ячейка Excel, в которой хранится значение объема капиталовложений за текущий год (в данном случае – первый расчетный год). 2) =B5*B4, где В5 – ячейка Excel, в которой хранится значение объема капиталовложений за текущий год (в данном случае – первый расчетный год); В4 – ячейка Excel, в которой хранится значение объема выпуска продукции за текущий год (в данном случае – первый расчетный год). За все остальные года расчеты (1-2) осуществляются по тому же алгоритму (см. рис. 2). 3) =СУММ(B4:K4), где В4:К4 – диапазон суммирования ячеек Excel, в которых хранятся значения объема выпуска продукции за весь расчетный период. 4) =СУММ(B5:K5), где В5:К5 – диапазон суммирования ячеек Excel, в которых хранятся значения объема капиталовложений за весь расчетный период. 5) =СУММ(B9:K9), где В9:К9 – диапазон суммирования ячеек Excel, в которых хранятся значения объема капиталовложений, возведенного в квадрат, за весь расчетный период. 6) =СУММ(B11:K11), где В11:К11 – диапазон суммирования ячеек Excel, в которых хранятся значения объема капиталовложений, умноженного на объем выпуска продукции, за весь расчетный период.
Расчет искомых коэффициентов уравнения линейной регрессии а1 (5) и а0 (6) осуществляем в Excel по формулам: 1) а1: =(L4-(L4-L11)/(B6-L5)*B6)/(L5-(L5-L9)/(B6-L5)*B6), где L4 – ячейка Excel, в которой хранится значение L5 – ячейка Excel, в которой хранится значение L9 – ячейка Excel, в которой хранится значение L11 – ячейка Excel, в которой хранится значение В6 – ячейка Excel, в которой хранится значение количества лет расчета (10);
2) а0: =(L4-L11-B14*(L5-L9))/(B6-L5), где L4 – ячейка Excel, в которой хранится значение L5 – ячейка Excel, в которой хранится значение L9 – ячейка Excel, в которой хранится значение L11 – ячейка Excel, в которой хранится значение В6 – ячейка Excel, в которой хранится значение количества лет расчета (10); В14 – ячейка Excel, в которой хранится значение а1.
Расчетные значения Yi по уравнению регрессии получаем в Excel по формулам (представлена формула для первого года расчетного периода): =$B$15+ $B$14*B5, где В5 – ячейка Excel, в которой хранится значение объема капиталовложений за 1 год расчета; $В$14 – ячейка Excel, в которой хранится значение а1 (для удобства дальнейших расчетов в Excel адрес этой ячейки фиксируется с помощью значка «$»); $В$15 – ячейка Excel, в которой хранится значение а0 (для удобства дальнейших расчетов в Excel адрес этой ячейки фиксируется с помощью значка «$»). По этому алгоритму осуществляются расчеты за остальные годы расчетного периода (см. рис. 2).
Для применения метода наименьших квадратов используем формулу: где В – суммарная оценка погрешности расчетов по методу наименьших квадратов; Yi – расчетные значения по уравнению регрессии по годам; уi – исходные значения объема выпуска продукции по годам. Погрешность расчета =(B18-B4)*(B18-B4), где В18 – ячейка Excel, в которой хранится расчетное значение объема выпуска продукции за 1 год расчета; В4 – ячейка Excel, в которой хранится исходное значение объема выпуска продукции за 1 год расчета. По этому алгоритму осуществляются расчеты за остальные годы расчетного периода (см. рис. 2). Суммарную погрешность расчета В за весь период вычислим в Excel по формуле: =КОРЕНЬ(СУММ(B20:K20)), где В20:К20 – диапазон суммирования ячеек Excel, в которых хранятся значения погрешности расчетов
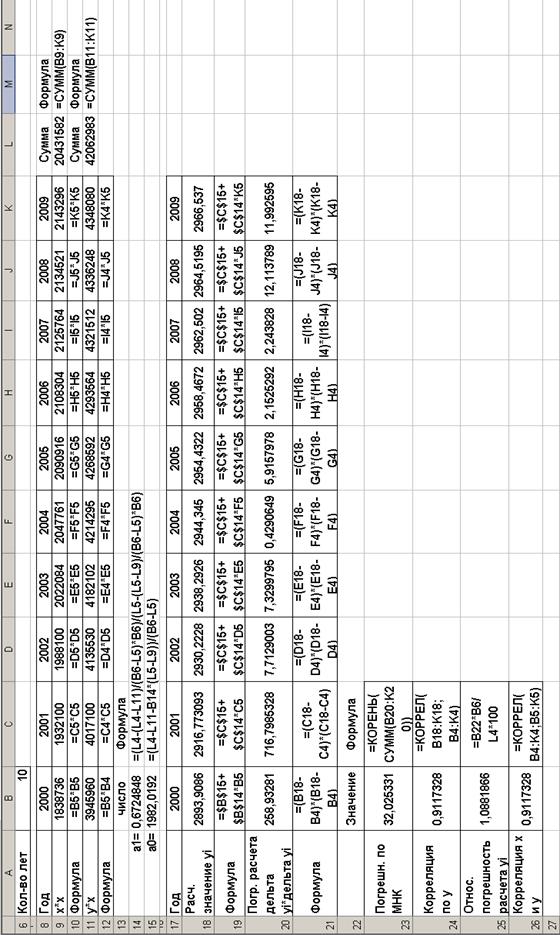
Рис. 2. Алгоритм расчетов по 2 заданию Суммарную относительную погрешность расчета Yi за период вычислим в Excel по формуле: =B22*B6/L4*100, где В22 – погрешность расчета за весь расчетный период по методу наименьших квадратов; В6 – ячейка Excel, в которой хранится значение количества лет расчета (10); где L4 – суммарный объем выпуска продукции за весь расчетный период. Парную корреляция по y за период вычислим в Excel по формуле: = КОРРЕЛ(B18:K18;B4:K4), где В18:К18 – диапазон ячеек Excel, в которых хранятся расчетные значения Yi за весь расчетный период; В4:К4 – диапазон ячеек Excel, в которых хранятся значения объема выпуска продукции за весь расчетный период. Парную корреляцию по х и y за период вычислим в Excel по формуле: =КОРРЕЛ(B4:K4;B5:K5), где В5:К5 – диапазон ячеек Excel, в которых хранятся значения объема капиталовложений за весь расчетный период; В4:К4 – диапазон ячеек Excel, в которых хранятся значения объема выпуска продукции за весь расчетный период. Алгоритм расчетов на листе Excel с указанием используемых формул и полученными результатами представлен на рисунке 2. Результаты расчетов позволяют сделать следующие выводы: · Высокое значение показателя парной корреляции (>0,91) и малая величина относительной погрешности прогнозирования (<1,09%) позволяют утверждать, что составленное уравнение регрессии (у=0,672484783387301 х+1982,01924453955) для рассматриваемого временного ряда имеет высокую степень достоверности прогноза; · Такие результаты объясняются высоким значением показателя парной корреляции для исходных временных рядов. yi и xi (>0,91).
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 97; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.101 (0.008 с.) |

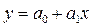 ;
;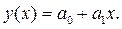 (3)
(3)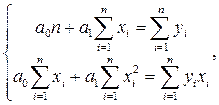 (4)
(4)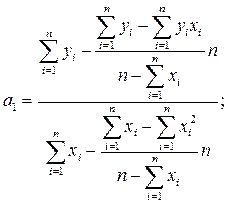 (5)
(5)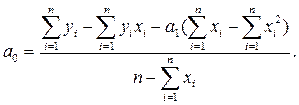 (6)
(6)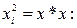
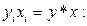
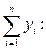
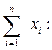
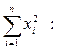
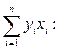
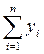 за весь расчетный период;
за весь расчетный период;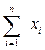 за весь расчетный период;
за весь расчетный период;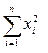 за весь расчетный период;
за весь расчетный период;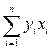 за весь расчетный период;
за весь расчетный период;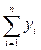 за весь расчетный период;
за весь расчетный период;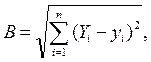 (7)
(7)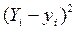 за первый год вычислим в Excel по формуле:
за первый год вычислим в Excel по формуле: