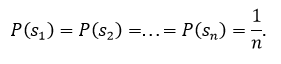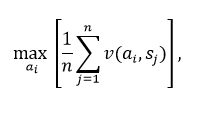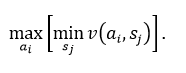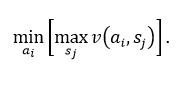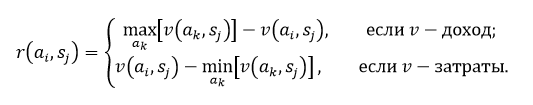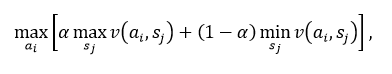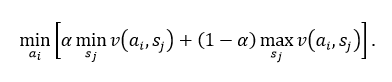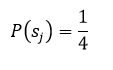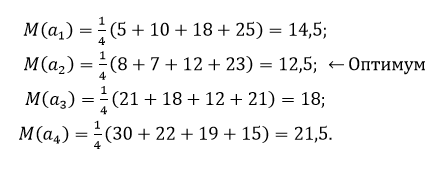Критерии принятия решений в условиях неопределенности

Для принятия решений в условиях неопределенности используется ряд критериев. Эти критерии отличаются по степени консерватизма, который проявляет лицо, принимающее решение, при выборе в условиях неопределенности.

Критерий Лапласа опирается на принцип, который гласит, что, поскольку распределение вероятностей состояний P (s_j) неизвестно, нет причин их считать различными. Следовательно, используется оптимистическое предположение, что вероятности всех состояний природы равны между собой, т.е.

 

Тогда при анализе матрицы прибылей, наилучшее решение находится по формуле:

где v (a_i, s_j) – элемент матрицы прибылей.

Если величина v (a_i, s_j)  представляет расходы лица принимающего решение, то оператор «max» меняется на «min».

Максиминный (минимаксный) критерий основан на осторожном поведении лица, принимающего решение, и сводится к набору наилучшей альтернативы из наихудших. Если величина v (a_i, s_j)  представляет получаемую прибыль, то в соответствии с максиминным критерием в качестве оптимального выбирается решение, обеспечивающее

 

 

Если величина v (a_i, s_j)  представляет затраты, используется минимаксный критерий, который определяется следующим соотношением

Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем замены матрицы платежей (выигрышей или погрешностей) v (a_i, s_j)  матрице потерь r (a_i, s_j)

В дальнейшем для анализа матрицы потерь используется минимаксный критерий.

Критерий Гурвица охватывает ряд различных подходов к принятию решений – от наиболее оптимистичного до наиболее пессимистичного. Если величины v (a_i, s_j)  представляют доходы, то решению соответствует

где параметр α – показатель оптимизма (0≤α≤1). При α=0 критерий Гурвица становится консервативным, так как его применение эквивалентно применению обычного минимаксного критерия. При α=1 критерий Гурвица становится оптимистичным, т.к. рассчитывает на наилучшие из наилучших условий. Степень оптимизма (или пессимизма) определяется выбором величины α.

Если v (a_i, s_j) выражают потери, критерий Гурвица принимает вид:

 

Принятие решений в условиях неопределенности

Проанализируем поставленную задачу с точки зрения четырех рассмотренных выше критериев.

 

Критерий Лапласа

При j = 1,2,3,4 вероятности

Тогда ожидаемые значения затрат для различных возможных решений вычисляются следующим образом:

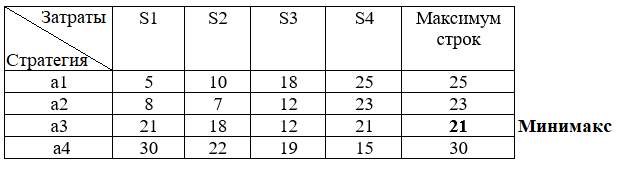
Минимаксный критерий

В виду того что анализируется матрица затрат, используется минимаксный критерий (табл. 2).

 

Таблица 2 – Модифицированная матрица затрат

 

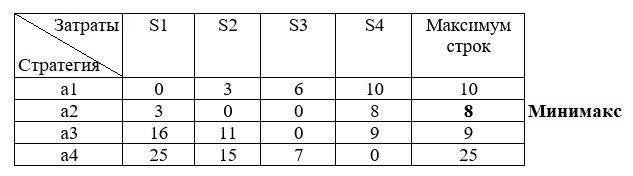
Критерий Сэвиджа

Определим матрицу потерь, путем вычитания чисел 5,7,12 и 15 из элементов столбцов от первого до четвертого соответственно (табл. 3).

 

Таблица 3 – Модифицированная матрица потерь

16

 

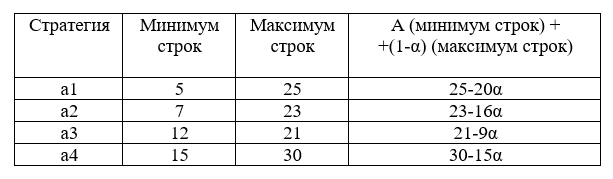
Критерий Гурвица

Расчет по критерию Гурвица приведен в табл. 4.

Таблица 4 – Выполнение расчетов по критерию Гурвица

Подставив α определим оптимальную стратегию. При α=0,5 оптимальными являются либо стратегия a1, либо а2. При α=0,25 оптимальным является решение а3.