
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2 Показатели центра распределенияСодержание книги Поиск на нашем сайте
1 Среднее арифметическое (М) 2 Среднее гармоническое (Мгар) 3 Среднее геометрическое (Мг) 4 Среднее квадратическое (Мкв) 5 Среднее кубическое (Мкуб) Для того чтобы получить достаточно обоснованное представление о генеральной совокупности на основании выборки, необходимо использовать наиболее характерные параметры признака. К ним относятся показатели среднего положения: непараметрические, т. е. менее точные (мода, медиана) и параметрические, т. е. более точные (средние величины: арифметическое, гармоническое, квадратическое, кубическое, геометрическое). Средняя величина выражает характерную, типичную для данного ряда величину признака и является равнодействующей всех факторов, влияющих на признак. В ней погашаются индивидуальные различия вариант в ряду, обусловленные случайными обстоятельствами. Рассмотрим параметрические показатели.
1 Среднее арифметическое (М) представляет собой величину, сумма положительных и отрицательных отклонений от которой равна нулю. Оно является основной характеристикой статистической совокупности. Для невзвешенного вариационного ряда среднее арифметическое вычисляется по формуле М где Σx – сумма всех вариант совокупности. Среднее арифметическое выборки характеризует среднее арифметическое генеральной совокупности, абсолютная и точная величина которого нам неизвестна. Для точности определения выборочных параметров необходимо установить величину ошибок репрезентативности. Ошибку среднего арифметического выборки обозначают индексом m м. Если m м =0, величина выборочной совокупности равна величине генеральной совокупности. Ошибка среднего арифметического выборки рассчитывается по формуле:
где σ – среднее квадратическое отклонение Пригодность среднего арифметического выборки для характеристики среднего арифметического генеральной совокупности определяется путем установления достоверности. Достоверность характеризует реализуемость некоторого события, подтверждая его осуществимость высокими значениями уровней вероятности (Р = 0,95; 0,99). Достоверность среднего арифметического оценивают по критерию Стьюдента:
Пример. Определено следующее количество осадков, выпавших в пяти пунктах наблюдений:25, 35, 40, 45 и 55мм (N =5). Определить среднее количество осадков. Решение:
2 Среднее гармоническое (M гар) используется при усреднении меняющихся скоростей протекания природных процессов и показателей обратно пропорциональной зависимости между природными процессами или явлениями. Среднее гармоническое для невзвешенного вариационного ряда определяется по формуле:
Пример. При измерении скорости ветра в течение суток были получены следующие результаты: 5,7,4,3,6,8, 9 м/с. Вычислить общий средний показатель скорости. Решение: Если среднюю скорость воды в реке рассчитывать по среднему арифметическому, то ее величина составит 6 м/с. Различие считается существенным в тех случаях, когда необходима высокая точность.
3 Среднее геометрическое(Мг) необходимо для расчета в случаях, когда требуется определить средние темпы прироста (например, сельскохозяйственной продукции или вегетативной массы деревьев за вегетационный период и т. д.). Этот показатель дает более точное представление о приросте по сравнению со средним арифметическим и рассчитывается по формуле:
Пример. Увеличение прироста зеленой массы клевера за май-август составило 20 и 25 ц/га. Найти средний прирост.
При наличии нулевого показателя вместо среднего геометрического вычисляется приближенное среднее арифметическое. 4 Среднее квадратическое (Мкв) используется, когда необходима проверка результатов эксперимента на единство суммарного действия (например, требуется определить средний радиус или диаметр исследуемого объекта). Для невзвешенного ряда используется формула:
Пример. Имеются данные по величине радиусов трех спилов дуба: 20, 24, 32, 28, 22 см. В данном случае вместо среднего арифметического при расчетах следует использовать среднее квадратическое:
5 Среднее кубическое (Мкуб) применяется в тех же случаях, что и среднее квадратическое, т. е. При проверке на единство суммарного действия (например, при нахождении объема), и определяется по формуле: Мкуб = Пример. Кубатура древесины по семи ключевым участкам составила 5, 7, 9, 13, 16, 19 и 20 м3. Среднее кубическое равно Мкуб = Эта величина существенно отличается от среднего арифметического. По абсолютной величине рассмотренные выше средние значения располагаются в следующем порядке: Мгар<=Мг<=М<=Мкв<=Мкуб. Степень различия между средними зависит от величины коэффициента вариации рассматриваемой совокупности: чем больше коэффициент вариации, тем сильнее различаются по величине показатели среднего положения.
Задания для самостоятельной работы 1 Территория региона площадью 1200 тыс. км2 разбита на 3 зоны, имеющие площади 450, 390 и 360 тыс. км2. Средняя плотность населения этих зон составляет соответственно 16,0; 13,5 и 15,1 чел./км2. Определить среднюю плотность населения по району в целом. 2 В изучаемом регионе находится всего 10 населенных пунктов. В одном из них проживает 120 человек, в двух по 260 человек, в 3 – по 73 человека и в одном – 34 и в трех – по 1500 человек. Найти среднюю численность населения в одном населенном пункте. 3 Имеются данные по радиусам спилов стволов березы: 14,16,19,24,28 см. Определить среднюю величину спилов. 4 Увеличение прироста зеленой массы клевера за май-август составило 10 и 35 ц/га. Определить средний прирост. 5 Кубатура строительного кирпича на участке составила 12, 14, 10, 15 и 20 м3. Определить среднее кубическое.
Вопросы для самоконтроля
1 С какой целью определяют показатели центра распределения? 1 Какие виды показателей средних вы знаете? 2 Чем отличаются показатели центра распределения? 3 Чем выражаются показатели среднего положения? 4 Что характеризуют показатели среднего положения? 5 Для чего рассчитываются достоверность того или иного показателя?
|
||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.68.97 (0.009 с.) |

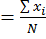 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3)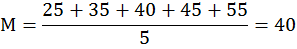
 (2.4)
(2.4)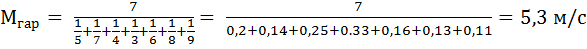 .
. (2.6)
(2.6)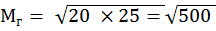 = 22,4 ц/га.
= 22,4 ц/га. (2.7)
(2.7)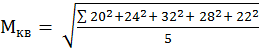 =
= 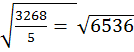 = 25,56 ≈ 26 см
= 25,56 ≈ 26 см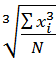 (2.8)
(2.8)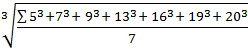 =
= 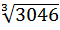 = 14,5 м3
= 14,5 м3


