Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
М. С. Томаш, Т. Г. Флерко, Ю. С. ЗезюлинаСодержание книги Поиск на нашем сайте
М. С. ТОМАШ, Т. Г. ФЛЕРКО, Ю. С. ЗЕЗЮЛИНА
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ГЕОГРАФИИ
Практическое руководство для студентов специальности 1-31 02 01-02 «География (научно-педагогическая деятельность)» Часть 1
Гомель ГГУ им.Ф.Скорины 2014 УДК ББК
Рецензенты: кандидат географических наук Е. Н. Карчевская; кандидат географических наук О. В. Шершнев
Рекомендовано к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины»
Практическое руководство включает тематику практических занятий, пояснительный материал с основными определениями и формулами для расчета показателей, примеры выполнения заданий и задачи для самостоятельной работы, вопросы для самоконтроля. Раскрыта сущность основных математических методов, применяемых в географических исследованиях для группировки, классификации объектов и выявления пространственных закономерностей. Адресовано студентам специальности «География (научно-педагогическая деятельность)».
УДК ББК
Содержание
Введение
Географические исследования и практические задачи базируются на большом объеме количественной информации, которую необходимо объективно оценить и провести группировку или классификацию, доказать зависимость или провести моделирование, выявить оптимальные условия развития или установить пространственные закономерности развития объектов или явлений, дать прогноз их развития. Решить эти задачи помогают математические и статистические расчеты. В процессе своего развития география накопила большое количество методов, но среди их многообразия на современном этапе резко выделяются по значимости и перспективам использования, интенсивно развивающиеся новейшие методы исследований. В первую очередь это математические методы, открывшие качественно новый этап в информационном обеспечении исследований в науках о Земле. Изучение математических методов – важный элемент профессиональной подготовки студентов высших учебных заведений специальности «География». Студенты-географы должны быть готовы к решению сложных проблем взаимодействия природы и общества. Для принятия практических шагов по улучшению территориальной организации природы, общества и хозяйственной деятельности необходимо владеть теоретическими знаниями, методами, приемами и методикой отраслевых и комплексных физико-географических и экономико-географических исследований. Целью проведения практических занятий по математическим методам в географии является приобретение студентами современных научных знаний о методиках оценки и анализа фактических данных, методах расчета основных математических и статистических показателей. Руководство включает тематику практических занятий, пояснительный материал с основными определениями и формулами для расчета показателей, примеры выполнения заданий и задачи для самостоятельной работы, вопросы для самоконтроля. В издании раскрыта сущность основных математических методов, применяемых в географических исследованиях для группировки, классификации объектов и выявления пространственных закономерностей. Данное практическое руководство предназначено в первую очередь для студентов геолого-географического факультета специальности «География (научно-педагогическая деятельность)», а также будет полезно учителям географии, преподавателям географических дисциплин средних специальных и высших учебных заведений, школьников и всех тех, кто интересуется географией, природопользованием и охраной природы.
Вопросы для самоконтроля
1 Что называется генеральной совокупностью и выборкой? 1 Какие виды выборок бывают? 2 Назовите правила составления выборок разных типов? 3 С какой целью используется критерий Стьюдента при составлении вариационных рядов? 4 Из каких географических данных можно составить вариационный ряд? 5 Каким способом определяется артефакт в вариационном ряду?
Вопросы для самоконтроля
1 С какой целью определяют показатели центра распределения? 1 Какие виды показателей средних вы знаете? 2 Чем отличаются показатели центра распределения? 3 Чем выражаются показатели среднего положения? 4 Что характеризуют показатели среднего положения? 5 Для чего рассчитываются достоверность того или иного показателя?
Вопросы для самоконтроля
1 Для чего используют показатели разнообразия признаков? 2 Какие показатели разнообразия признаков вы знаете? 3 Какие показатели используют как составляющие параметры нормального распределения? 4 Что показывает среднее квадратическое отклонение? 5 На что указывает дисперсия? 6 Что представляет собой коэффициент вариации? 7 Каким бывает разброс вариант в зависимости от значения коэффициента вариации?
Критерий Стъюдента (t) Критерий Фишера (F) 4 Критерий соответствия (χ2)
Достоверность различий между генеральными совокупностями (Ni, N 2...) может быть определена с помощью следующих критериев достоверности: критерия Стьюдента (t), наименьшей существенной разности (НСР), критерия соответствия (χ2), критерия Фишера (F).
1Критерий Стьюдента. Сравнение выборочных совокупностей по критерию Стьюдента t позволяет утверждать с некоторой долей уверенности сходство или различие между средними выборок по разнице между ними с использованием формулы
где d – разность между средними (М1 – М2); т d – ошибка разности средних. Выделяют три типа сравниваемых статистических совокупностей: независимые с одинаковым объемом выборок (N 1 = N 2), независимые с разным объемом выборок (N 1 Независимые статистические совокупности могут быть получены на одной или нескольких точках, но при одинаковых условиях проведения эксперимента: например, измерение температуры воздуха в июле в г. Минске в течение нескольких лет и установление достоверных различий между этими показателями по годам исследований; определение содержания бора в автономных ландшафтах. Поэтому при установлении степени свободы в каждом независимом эксперименте выборочные совокупности суммируются. Сопряженные статистические совокупности, как и независимые, однозначны по смыслу, их получают при проведении исследований на одном или нескольких ключах, но в разных условиях. Например: измерение температур воздуха и почвы на глубине 5 см в г. Минске в июле и сравнение полученных показателей (условия разные, точка наблюдения одна и та же); Степень свободы в каждом рассматриваемом эксперименте определяется по числу пар сравниваемых выборок (Nu). Рассмотрим расчеты достоверности различий для одинакового и разного объемов выборок.
Пример 1. При исследовании глубины расчленения рельефа в Воложинском районе N 1 и Браславском районе N 2 необходимо установить, объединять рассматриваемые участки в один геоморфологический район по степени расчленения рельефа или различать их как самостоятельные. Воложинский район – 20, 17, 16, 15, 15; Браславский район – 17,16, 15, 14, 14. (N1 = N2) 1) Находим среднее арифметическое для каждой выборки
Таблица 2 – Форма обработки вариант в независимых совокупностях
2) Находим разность между средними d =М1 – M 2 (4.2) d = 16,6 – 15,2 = 1,4 м При расчете разницы между средними из большей величины вычитают меньшую независимо от нумерации выборочных совокупностей. 3) Затем находят ошибки средних для каждой выборки в отдельности по формуле
4) Находим ошибку разности между средними по формуле:
5) Число степеней свободы устанавливают следующим образом: v = N 1 + N 2 – 2 (4.5) v= 5 + 5 – 2 = 8 6) Определяем Критерий Стьюдента
Сопоставляем табличные значения критерия Стьюдента tт=2,32 и 3,36 (см. приложение 4) при Р=0,95 и 0,99 для v=8 с расчетным. Поскольку tТ > t Ф,, то разность между средними признается несущественной (недостоверной). Следовательно, при выделении геоморфологических районов по глубине расчленения рельефа рассматриваемые участки необходимо объединить в один геоморфологический район.
Пример 2. При исследовании глубины расчленения рельефа в Воложинском районе N 1 и Браславском районе N 2 необходимо установить, объединять рассматриваемые участки в один геоморфологический район по степени расчленения рельефа или различать их как самостоятельные. Воложинский район – 20, 17, 16, 15, 15; Браславский район – 17,16, 15, 14, 14, 16. (N1 ≠ N2) 1) Находим среднее арифметическое для каждой выборки
Таблица 2 – Форма обработки вариант в независимых совокупностях
2) Находим разность между средними d =М1 – M 2 = 16,6 – 15,3 = 1,3 м 3) Ошибка разности средних, определяется по формуле
где Σ(x1 – M1)2 – сумма квадратов отклонений от среднего для первой выборки; Σ (х2 –М2)2 – второй выборки; N1, N2– количество вариант в первой и второй выборках соответственно;
4) Число степеней свободы для разного объема выборок устанавливают следующим образом:
m1, m2— ошибка среднего первой и второй выборок соответственно
5) Определяем Критерий Стьюдента
Сопоставляем табличные значения критерия Стьюдента tт=2,45 и 3,71 (приложение 4) при Р=0,95 и 0,99 для v=6 с расчетным. Поскольку tТ > t Ф,, то разность между средними признается несущественной (недостоверной)
Пример 3. Получены сопряженные выборки только с одинаковым объемом конечно-моренного ландшафта N 1 и донно-моренного ландшафта N 2. Число пар N П = 5. Воложинский район – 20, 17, 16, 15, 15; Браславский район – 17,16, 15, 14, 14 ( N 1 = N 2). 1) Находим среднее арифметическое для каждой выборки
Таблица 3 – Форма обработки данных сопряженных наблюдений
2) Находим разность между средними
3) Находим ошибку разности между средними по формуле:
где di – разность между индивидуальными сопряженными вариантами в выборках;
4) Число степеней свободы устанавливают следующим образом: v = NП – 2 (4.15) v= 5 – 2=3 5) Определяем Критерий Стьюдента
Сопоставляем табличные значения критерия Стьюдента tт=3,18 и 5,84 (приложение 4) при Р=0,95 и 0,99 для v=3 с расчетным. Поскольку t Ф > tТ при Р=0,95,то разность между средними признается существенной (достоверной). Следовательно, при выделении геоморфологических районов по глубине расчленения рельефа рассматриваемые участки необходимо рассматривать как самостоятельные.
2 Критерий наименьшей существенной разности (НСР) показывает то минимальное различие между средними, начиная с которого при выбранном уровне вероятности средние сравниваемые показатели существенно отличаются друг от друга. Величина критерия НСР выражается в тех же единицах, что и сравниваемые средние выборочных совокупностей, и определяется по формуле: где т d – ошибка разности средних; tT – табличное значение критерия Стьюдента при выбранном значении уровня вероятности. Если разность между сравниваемыми средними в условиях эксперимента больше или равна величине НСР при Р = 0,95 или 0,99, то различие существенно. Если разность между средними меньше НСР, то различие обусловлено случайными факторами и признается недостоверным. Проверим достоверность разности между средними арифметическими с использованием критерия НСР для случаев независимого и сопряженного наблюдений по формуле: НСР0,95 = 2,32 • 1,1 = 2,55 м, НСР0,99 = 3,36• 1,1 = 3,696 м для независимых наблюдений; НСР0,95 = 3,18 • 0,40= 1,27 м, НСР0,99 = 5,84 •,40 = 2,34 м для сопряженных наблюдений. По величине НСР достоверное различие между средними установлено лишь при сопряженном наблюдении для уровня вероятности 0,95 (HCP0,95=1,27<
3 Критерий Фишера (F) используется для установления достоверностиразличия между совокупностями по дисперсиям. В таких случаях лучше использовать критерий Фишера F (положительное асимметричное распределение). Расчет критерия Фишера производится по формуле: где Если величина расчетного критерия Фишера FФ не превышает величины приведенного в таблице FT (приложение 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф > Fт эти дисперсии достоверно различны, а различие сравниваемых генеральных совокупностей признается неодинаковым. Степень свободы рассчитывается для сравниваемых совокупностей отдельно по формуле v = N – 1.
Пример. Необходимо установить достоверность различия в содержании гумуса в дерново-подзолистой заболоченной суглинистой почве для северной n 1 и центральной n 2 провинций РБ. Количество вариант в обеих совокупностях одинаковое. В результате обработки данных получены следующие средние и дисперсии: M1 = 3,53 %, Fф =
Степень свободы равна: v1 = 5—1=4, v2 = 5—1=4. Для P=0,95 и 0,99 FT = 6,39 и 15,98 (приложение 5) соответственно. Поскольку Fф>Fт, то различие в содержании гумуса по провинциям признается существенным при уровне вероятности Р=0,95. 4 Критерий соответствия (χ2) - количественное изучение явлений требует создания гипотез, с помощью которых можно объяснить эти явления. Для этой цели используется критерий кси-квадрат (χ2), или критерий соответствия, который рассчитывается по формуле
где φ, φ' – число наблюдений в опыте фактическое и теоретически ожидаемое. Если расчетные значения кси-квадрат превышают табличные (приложение 6), то гипотеза о независимости признаков отвергается. Если Степень свободы при проверке гипотезы о нормальном распределении вычисляется по формуле v = k –3 (4.19) где k – число классов. Достоверность расчетных данных можно также оценить по формуле: Различие считается достоверным, если D
Пример. Следует определить число сельских жителей с бронхолегочными заболеваниями, обострение болезни у которых связано с природными условиями местожительства. Для обработки выборочных вариант составляем таблицу. Всего выявлен 71 больной житель из 639 обследованных одного возраста и пола по 9 человек в каждом населенном пункте. Таблица 4 - Сравнение эмпирических и теоретических частот с использованием критерия кси-квадрат
Для обработки данных количество обследованных сгруппировано в 9 классов. Поскольку частота в каждом классе φ, φ' должна быть не менее 5, объединяем первые три и последние два класса в столбцах 2 и 3. Получаем новые классы с частотами 11,15 и 13,8 (всего по 6 классов распределения). Затем производим расчеты, которые позволяют получить критерий Сравниваем Определим также достоверность
Полученная величина D=0,99<3, следовательно, рассчитанное значение
Задания для самостоятельной работы 1 Необходимо установить достоверность различия в содержании гумуса в дерново-подзолистой заболоченной суглинистой почве для северной N1 и центральной N2 провинций РБ. Количество вариант в обеих совокупностях одинаковое. В результате обработки данных получены следующие средние и дисперсии: М1= 4,223 %, σ12= 2,055 %; М2= 3,15 %, σ22= 22,1 %; N = 15. 2 Сравнить глубину расчленения рельефа в пределах конечно-моренного ландшафта N1 и донно-моренного ландшафта N2 (получены сопряженные выборки). Исходные данные представлены в таблице 2. 3 При исследования глубины расчленения рельефа в двух районах Беларуси N1 и N2 необходимо установить, объединять рассматриваемые участки в один геоморфологический район по степени расчленения рельефа или различать их как самостоятельные. Данные приведены в таблице 2.
Таблица 2
4 Собрав данные о городах юго-запада Англии с числом жителей 8-12 тыс. в каждом, обнаружено, что число антикварных магазинов выше среднего (5) в тех городах, где высока доля пенсионеров. Таблица 1 показывает полученное распределение частот. Таблица 1 – Наблюдаемое и теоретическое распределение антикварных магазинов по группам городов, сгруппированных с учетом доли пенсионеров в их населении
Проверить, правильно ли утверждение.
5 Существует гипотеза, что распределение пастбищ не зависит от высоты местности над уровнем моря. Доказать или опровергнуть гипотезу. Оценить достоверность расчетов. Данные представлены в таблице 3 Таблица 3
Вопросы для самоконтроля
1 Назовите основные статистические критерии различия? 2 Какие виды выборок используются для обработки с помощью критериев различия? 3 Что показывает критерий НСР? 4 С какой целью используется критерий Стьюдента при обработке выборок различного объема? 5 По какому критерию устанавливаются различия между выборочными совокупностями? 6 Какой критерий доказывает или опровергает выдвинутую гипотезу?
Приложение 1 Таблица 1 - Таблица достаточно больших чисел
Приложение 2 Таблица 2 - Случайные числа
Приложение 3
Таблица 3 - Значение критерия τ в зависимости от объема выборки N и уровня значимости α
Приложение 4 Таблица 4 - Значения критерия Стьюдента t при различных уровнях значимости
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.152 (0.014 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 (4.1)
(4.1)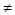 N 2), сопряженные только с одинаковым объемом выборок (N 1 = N 2).
N 2), сопряженные только с одинаковым объемом выборок (N 1 = N 2).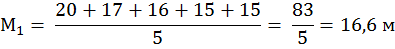
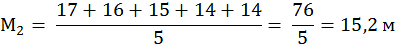
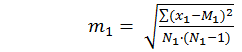
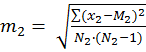 (4.3)
(4.3)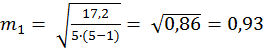
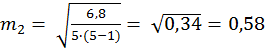
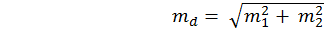 (4.4)
(4.4)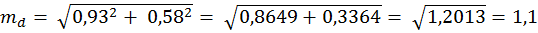
 (4.6)
(4.6)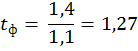
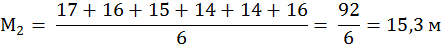
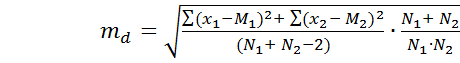 (4.7)
(4.7)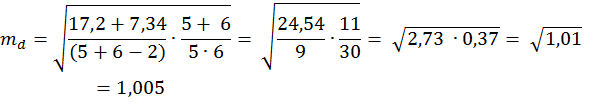
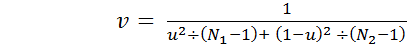 (4.8)
(4.8) (4.9)
(4.9)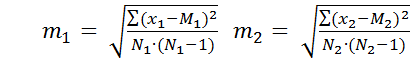 (4.10)
(4.10)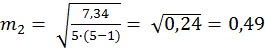
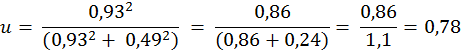
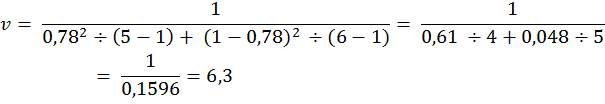
 (4.11)
(4.11)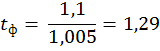
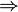 рассматриваемые участки необходимо объединить в один геоморфологический район.
рассматриваемые участки необходимо объединить в один геоморфологический район.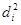
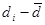
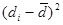
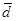 = l,4
= l,4
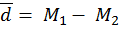 (4.12)
(4.12) = 16,6 –15,2=1,4
= 16,6 –15,2=1,4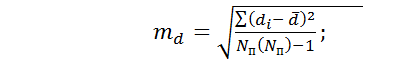 (4.13)
(4.13)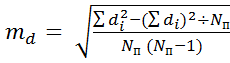 (4.14)
(4.14)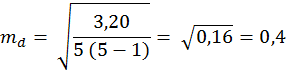
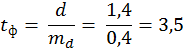
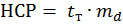 (4.16)
(4.16) = 1,4 м).
= 1,4 м).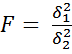 (4.17)
(4.17)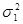 по абсолютной величине должна быть больше, чем
по абсолютной величине должна быть больше, чем 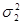 .
.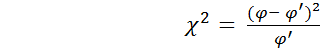 (4.18)
(4.18)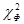 <
<  , то признаки можно считать независимыми.
, то признаки можно считать независимыми.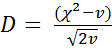 (4.20)
(4.20)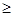 3. При обработке данных по условиям применения критерия кси-квадрат требуется, чтобы частота в каждом классе была не менее пяти.
3. При обработке данных по условиям применения критерия кси-квадрат требуется, чтобы частота в каждом классе была не менее пяти. 10
15
12
10
10
15
12
10
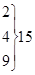 13
14
10
11
13
14
10
11
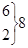
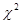 =5,43
=5,43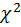 (см. таблицу).
(см. таблицу).