Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное произведение двух векторов. Теорема. Свойства векторного произведения
Теорема. Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения. Свойства векторного произведения: 1. 2. 3. 4. 5. 21. Выражение координат векторного произведения через координаты векторов
22. Смешанное произведение трех векторов. Свойства. Теорема о компланарности трех векторов Теорема о компланарности трёх векторов. Если смешанное произведение трёх не нулевых векторов равно нулю, то эти вектора компланарные. Свойства смешанного произведения трёх векторов: 1. 2. Условия компланарности трёх векторов: 1. если смешанное произведение трёх не нулевых векторов равно нулю; 2. если они линейно-независимы; 3. если среди них не более двух линейно-независимых векторов; 23. Выражение смешанного произведения через координаты векторов
· ·
Базис на плоскости и в пространстве. Теоремы 1-4 Базис на плоскости – это любые два линейно-независимых вектора. Теорема 1. Для того, чтобы два вектора на плоскости были линейно-независимы необходимо и достаточно, чтобы они были коллинеарны. Теорема 2. Для того, чтобы три векторы были линейно-зависимы, необходимо и достаточно, чтобы они были компланарны. Пусть Базис в пространстве – это любые три линейно-независимых вектора. Теорема 3. Для того, чтобы три вектора в пространстве были линейно-независимы, достаточно чтобы они были некомпланарны (т.е. не лежали на одной прямой или на параллельных прямых). Теорема 4. Любые четыре вектора в пространстве линейно-зависимы. (Например: Прямоугольно декартова система координат на плоскости. Задачи, решаемые методом координат на плоскости Возьмём на плоскости две пересекающиеся под прямым углом оси. Точку пересечения осей обозначим через O. Пусть координаты этой точки будут (0;0). Возьмём на осях единичные векторы · · Положение любой точки относительно выбранной системы координаты будет задаваться выбранными числами: абсциссой
Задачи, решаемые методом координат на плоскости: · Расстояние между двумя точками: пусть даны две точки: · Задача о делении отрезка в заданном отношении: пусть
o o o o o o o Аналогичными рассуждениями получаем Полярная система координат · Рассмотрим · Соединим · Пусть · Пусть угол между · · · ·
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 58; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.247 (0.01 с.) |

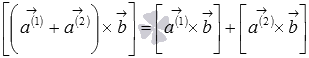
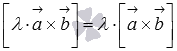

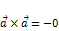

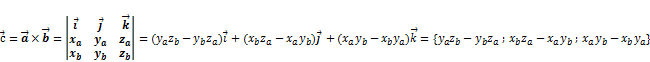
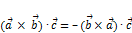
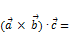

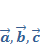 .
.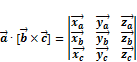

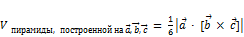
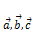 линейно-зависимы, тогда в силу теоремы 2 следует, что
линейно-зависимы, тогда в силу теоремы 2 следует, что  , где
, где 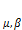 – числа. Это и есть разложение вектора
– числа. Это и есть разложение вектора  по векторным базисам
по векторным базисам 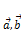 , где
, где 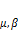 представляют собой координаты вектора
представляют собой координаты вектора 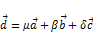 )
)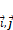 , которые определяют ортогональный базис (его векторы попарно ортогональны и равны единице), в самом деле векторы линейно-независимы.
, которые определяют ортогональный базис (его векторы попарно ортогональны и равны единице), в самом деле векторы линейно-независимы.
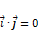
 и ординатой
и ординатой  .
.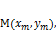
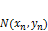 , тогда
, тогда 
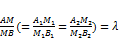 , даны B (xb, yb) и A (xa, ya). Найти M(x, y).
, даны B (xb, yb) и A (xa, ya). Найти M(x, y).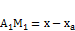 ,
, 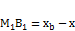

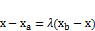
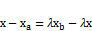
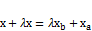

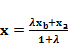
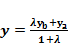 .
.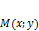 , заданную в прямоугольно-декартовой системе координат на плоскости.
, заданную в прямоугольно-декартовой системе координат на плоскости.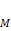 c началом координат (
c началом координат ( ) и рассмотрим
) и рассмотрим 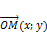 .
.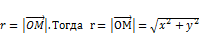 .
. и осью
и осью  равен
равен  .
.