
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости в отрезках. Теорема ⇐ ПредыдущаяСтр 7 из 7
Доказательство: · · · · Плоскость пересекает координатные оси в точках с координатами Параметрические уравнения плоскости. Теорема
Доказательство: · Пусть · Выберем на плоскости произвольную точку · · Если
· Записав разложение вектора Частные случаи расположения плоскости относительно прямоугольно-декартовой системы координат. Теорема Теорема. Пусть дана плоскость · · · · · · · · · · Взаимное расположение двух плоскостей в пространстве. Теоремы 1-3 Теорема. Пусть даны две плоскости: · · ·
Уравнение прямой, проходящей через данную точку в заданном направлении. Параметрические уравнения прямой. Теорема Теорема. Пусть прямая
В параметрической форме:
Доказательство: · Произвольная точка · Так как Уравнения прямой, проходящей через две заданные точки в пространстве. Теорема Теорема. Пусть точки
Доказательство: 1. Если за направляющий вектор Взаимное расположение двух прямых в пространстве. Теоремы 1-4 Теоремы. Пусть относительно прямоугольно-декартовой системы координат в пространстве заданы две прямые своими уравнениями: 1. 2. 3. 4. Взаимное расположение прямой и плоскости в пространстве. Теоремы 1-2 Теоремы. Пусть относительно прямоугольно-декартовой системы координат в пространстве заданы плоскость
1. 2. 3. Прямая как линия пересечения двух плоскостей. Теорема Пусть относительно прямоугольно-декартовой системы координат заданы две плоскости:
Теорема. Геометрический смысл неравенства первой степени с тремя неизвестными Плоскость · ( · (
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 39; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.136.170 (0.017 с.) |
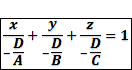
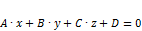
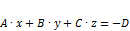


 ,
,  ,
,  .
.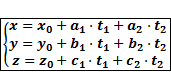
 и
и 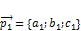 компланарны плоскости, а
компланарны плоскости, а 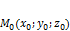 лежит на этой плоскости.
лежит на этой плоскости. .
. – компланарны.
– компланарны.
 по координатам получаем параметрическое уравнение прямой.
по координатам получаем параметрическое уравнение прямой. . Тогда:
. Тогда: , когда
, когда 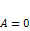 ;
; ;
; ;
;
 , когда
, когда  ;
; , когда
, когда  ;
; ;
; ;
; , когда
, когда 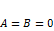 ;
; , когда
, когда 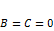 ;
;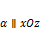 , когда
, когда  .
. и
и 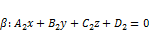 . Тогда:
. Тогда: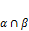 , когда
, когда  ;
;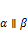 , когда
, когда  ;
; , когда
, когда  .
.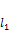 , коллинеарный ненулевому вектору
, коллинеарный ненулевому вектору  , проходит через
, проходит через 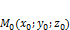 , тогда уравнение прямой проходящей через заданную точку и ненулевой вектор задаётся уравнением:
, тогда уравнение прямой проходящей через заданную точку и ненулевой вектор задаётся уравнением: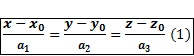
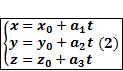
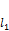 тогда и только тогда, когда
тогда и только тогда, когда  , что равносильно уравнению (1).
, что равносильно уравнению (1). . Записав это уравнение в координатной форме, мы получаем (2).
. Записав это уравнение в координатной форме, мы получаем (2). и
и  лежат на прямой
лежат на прямой 
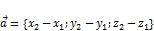 коллинеарный
коллинеарный 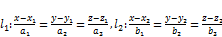 . Тогда
. Тогда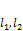 – скрещивающиеся, если
– скрещивающиеся, если 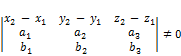 ;
; , если
, если 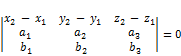 ;
;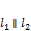 , если
, если  но
но 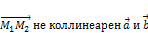 ;
;
 .
.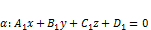 и прямая
и прямая 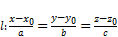 . Тогда:
. Тогда: , если
, если 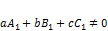 ;
;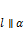 , если
, если  и
и 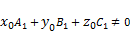 ;
; , если
, если 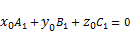 .
.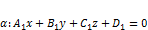 и
и 
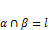 .
. задаётся своим каноническим уравнением
задаётся своим каноническим уравнением  , где
, где 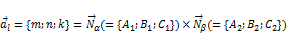 .
.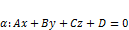 делит пространство на два полупространства:
делит пространство на два полупространства: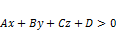 ) положительно-ориентированное;
) положительно-ориентированное;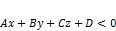 ) отрицательно-ориентированное.
) отрицательно-ориентированное.


