
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскость в пространстве. Уравнение плоскости, проходящей через точку и два неколлинеарных вектора. Теорема
Уравнение плоскости в пространстве – это линейное уравнение первой степени относительно неизвестных Теорема. В прямоугольно-декартовой системе координат уравнение плоскости, проходящий через точку
Доказательство: · Пусть · Возьмём на плоскости произвольным образом точки · Верно и обратное утверждение. Всякое решение уравнения (1) определяет точку с координатами Общее уравнение плоскости · Разложим по первой строке доказанную в прошлой теме теорему:
· Введём обозначения:
· Обозначим через · Имеем общее уравнение плоскости:
Здесь Верно и обратное утверждение. Всякое решение (2) определяет точку с координатами Замечание: вектор · Возьмём две лежащие на плоскости точки: · Координаты этих точек должны удовлетворять (2):
· Вычтем из (4) (3):
· Это равенство, по сути, представляет собой скалярное произведение, равное нулю:
· · Так как 38. Критерий компланарности вектора и плоскости. Теорема Теорема. Пусть относительно прямоугольно-декартовой системы координат заданы вектор
Доказательство: · Отложим вектор · Конец Р отложенного вектора будет иметь координаты · Вектор коллинеарен заданной плоскости тогда и только тогда, когда точка Р лежит в данной плоскости, т.е. выполняется уравнение (2):
· · После раскрытия скобок с учётом уравнения выше остаётся условие:
Из этой теоремы следует, что главный вектор плоскости 39. Уравнение плоскости, проходящей через 2 заданные точки и компланарной ненулевому вектору. Теоремы 1-3
Теорема. Пусть относительно прямоугольно-декартовой системы координат заданы две точки
Доказательство: · Пусть три точки · Векторы с координатами · Следовательно, матрица из их координат равняется 0. Обратная теорема. Всякое решение уравнения (1) определяет точку с координатами Теорема: Пусть относительно прямоугольно-декартовой системы координат заданы
Доказательство: · Пусть · Возьмём произвольным образом точку · Следовательно, определитель, составленный из их координат, равен 0 ч.т.д. Обратная теорема. Всякое решение уравнения (2) определяет точку, лежащую на плоскости.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.9.115 (0.006 с.) |
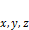 .
.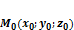 и два неколлинеарных вектора
и два неколлинеарных вектора  ;
; 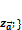 и
и  ;
; 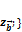 задаётся:
задаётся: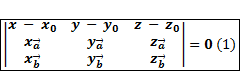
 ;
; 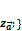 и
и 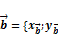 ;
;  лежат в одной плоскости.
лежат в одной плоскости. и составим
и составим  .
. ,
,  ,
, 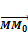 – компланарны, следовательно, их смешанное произведение равно 0:
– компланарны, следовательно, их смешанное произведение равно 0: 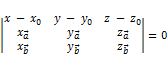 ч.т.д.
ч.т.д.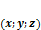 , лежащую на плоскости.
, лежащую на плоскости.


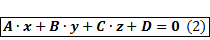
 , так как векторы
, так как векторы  ;
; 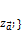 и
и 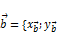 ;
; 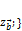 не коллинеарны, а значит определители в разложении одновременно не равны нулю для
не коллинеарны, а значит определители в разложении одновременно не равны нулю для 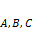 .
.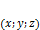 , лежащую на плоскости.
, лежащую на плоскости.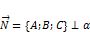 , где
, где  – плоскость, заданная (2). Доказательство:
– плоскость, заданная (2). Доказательство: и
и 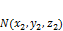 .
.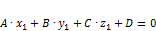 (3)
(3) (4)
(4)

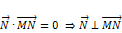
 , то
, то 
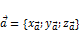 и плоскость, заданная (2). Тогда необходимое и достаточное условие компланарности вектора
и плоскость, заданная (2). Тогда необходимое и достаточное условие компланарности вектора  и данной плоскости имеет вид:
и данной плоскости имеет вид: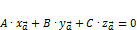
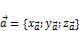 от произвольной точки
от произвольной точки 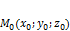 заданной плоскости.
заданной плоскости. .
. .
.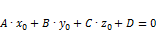 .
. .
.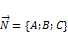 , заданной общим уравнением плоскости относительно общей декартовой системы координат, не компланарен этой плоскости:
, заданной общим уравнением плоскости относительно общей декартовой системы координат, не компланарен этой плоскости:  .
. и
и  и ненулевой вектор
и ненулевой вектор 
 ,
,  точка с координатами
точка с координатами 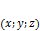 , а также
, а также  .
.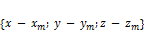 ,
,  ,
,  ,
,  . Тогда уравнение плоскости, проходящей через три точки, не лежащие на одной прямой:
. Тогда уравнение плоскости, проходящей через три точки, не лежащие на одной прямой:
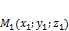 ,
,  ,
, 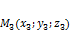 лежат на одной плоскости.
лежат на одной плоскости. , лежащую на плоскости, тогда векторы
, лежащую на плоскости, тогда векторы  ,
, 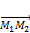 ,
, 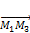 коллинеарны, так как лежат в одной плоскости.
коллинеарны, так как лежат в одной плоскости.


