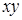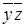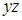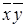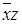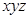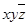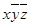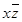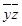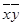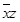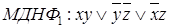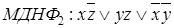Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полнота системы булевых функцийСодержание книги Поиск на нашем сайте
Для начала дадим основные определения. Определение. Говорят, что булева функция сохраняет 0, если f (0,0,…,0)=0. Определение. Говорят, что булева функция сохраняет 1, если Определение. Функция, реализуемая формулой Функцию, двойственную к функции Определение. Говорят, что булева функция самодвойственная, если Определение. Если для любого Например, Определение. Говорят, что булева функция Определение. Говорят, что булева функция линейна, если в ее каноническом полиноме Жегалкина коэффициенты при всех слагаемых, содержащих произведения переменных, равны 0. Для того чтобы система булевых функций обладала полнотой, она должна не сохранять ноль, единицу, не быть самодвойственной, монотонной и линейной. ПРИМЕР. Является ли система булевых функций Чтобы убедиться в функциональной полноте, составим таблицу, столбцы которой соответствуют классам
Как видно из таблицы, для каждой пары классов найдется функция, принадлежащая одному классу из пары и не принадлежащая другому Определение. Система функций B называется базисом, если: 1. B – полна; 2. при удалении из системы B хотя бы одной функции, полнота теряется.
ПРИМЕРЫ. 1. 2. 3. 4. 5.
Минимизация высказываний методом Квайна
1. Выражение из произвольной формы приводится к СДНФ. 2. Выполнив в СДНФ все возможные неполные склеивания, а затем все возможные поглощения мы получим Сокращенную ДНФ (СкДНФ). Конъюнкции в СкДНФ называются импликантами.
ПРИМЕР. Минимизировать функцию
Решение. Воспользуемся алгоритмом метода Квайна. 1. Получить СДНФ. 2. Получить сокращенную ДНФ (СкДНФ), используя следующие равносильности:
3. Построить импликантную матрицу, с помощью которой получить МДНФ. 1.
1 2 3 4 5 6 2. Применяя операции склеивания, получаем СкДНФ.
3. Составляем импликантную матрицу
Выбираем импликанты, которые поглощают все конституенты единицы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.97.131 (0.008 с.) |

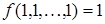 .
.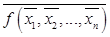 , называется двойственной к функции
, называется двойственной к функции 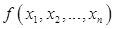 .
.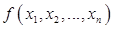 , обозначают
, обозначают 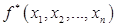 , т.е.
, т.е. 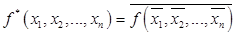 .
.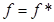 .
.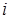
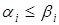 (
(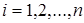 ), то говорят, что вектор
), то говорят, что вектор  предшествует вектору
предшествует вектору 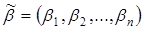 и пишут
и пишут 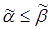 .
.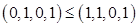 ;
; 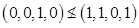 .
.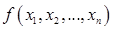 монотонна, если для любых наборов
монотонна, если для любых наборов 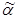 и
и 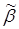 значений переменных, таких что
значений переменных, таких что 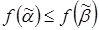 .
. полной?
полной?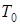 ,
, 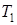 ,
, 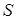 ,
, 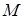 ,.
,. 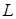 , строки – функциям
, строки – функциям 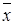
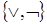 – дизъюнктивный базис Буля.
– дизъюнктивный базис Буля.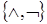 – конъюнктивный базис Буля.
– конъюнктивный базис Буля.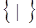 – базис Шеффера.
– базис Шеффера.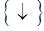 – базис Пирса.
– базис Пирса.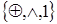 – базис Жегалкина.
– базис Жегалкина. 3. На основании СкДНФ и СДНФ строим импликантную матрицу и путем нахождения минимального покрытия этой матрицы получаем минимальную дизъюнктивную нормальную форму (МДНФ).
3. На основании СкДНФ и СДНФ строим импликантную матрицу и путем нахождения минимального покрытия этой матрицы получаем минимальную дизъюнктивную нормальную форму (МДНФ).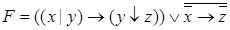
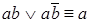 – склеивание;
– склеивание;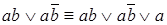 – неполное склеивание;
– неполное склеивание;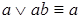 – поглощение.
– поглощение.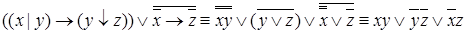 - ДНФ
- ДНФ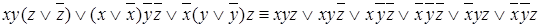 - СДНФ
- СДНФ