
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы алгебры логики. Функции алгебры логикиСодержание книги Поиск на нашем сайте
Предварительно вспомним некоторые определения из теории множеств. Множество – фундаментальное неопределяемое понятие. Множество – это совокупность объектов, которые, с одной стороны, различны и отличны друг от друга, а с другой стороны воспринимаются как единое целое. Пусть А и В – два множества и < a, b > – упорядоченная пара, где первый элемент Функция – это такое отношение, что из ПРИМЕР. А={1,2,3,4,5} B ={1,4,9,16,25}
f ={<1,1>, <2,4>, <3,9>, <4,16>, <5,25>} – это функция, где b = a 2. Теперь перейдем к определению булевых функций. Отличительной особенностью логических функций состоит в том, что они принимают значения в конечных множествах. Иначе говоря, область значений логической функции всегда представляет собой конечную совокупность чисел, символов, понятий, свойств и, вообще, любых объектов. Если область значений функций содержит k различных элементов, то она называется k -значной функцией. Определение. Логическая функция – это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b). Определение. Функцией алгебры логики (ФАЛ) называется функция, дающая однозначное отображение Х в Y. Замечание 1. Число различных ФАЛ, зависящих от n аргументов, конечно и равно Замечание 2. ФАЛ f(x1, x2, …, xi, xi+1, …, xn-1, xn) существенно зависит от аргумента xi, если имеет место соотношение f(x1, x2, …, xi-1,0, xi+1, …, xn-1, xn) ¹ f(x1, x2, …, xi-1,1, xi+1, …, xn-1, xn) в противном случае говорят, что от xi функция зависит не существенно и xi является ее фиктивным аргументом. ФАЛ не изменяется, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые являются фиктивными. Как найти несущественные аргументы? Для этого, если ФАЛ задана таблично, поступают следующим образом.
Разбивают множество наборов аргументов функции на два подмножества: - подмножество, на котором заданная функция принимает значение 1; - подмножество, на котором заданная функция принимает 0. Для проверки фиктивности аргумента xi вычеркивают столбец, ему соответствующий, и проверяют, не появились ли в обоих подмножествах одинаковые наборы. Если таких наборов не появилось, то xi является фи ПРИМЕР. Таблица
Произведем разбиение набора аргументов:
0 0 0 0 0 0 0 1 x1 x2 x3 x4
0 0 1 1 наборы х 0 1 0 1 0 1 1 0 на которых 1 1 0 0 f( 0 1 1 1 f( 1 0 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 0 1 1
Вычеркнем в наборах четвертый столбец. Оставшиеся наборы таковы, что ни один из них не входит одновременно в оба подмножества. Это свидетельствует о фиктивности аргумента x4.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.196.242 (0.009 с.) |

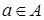 , а второй элемент
, а второй элемент 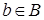 . Декартово произведение
. Декартово произведение 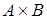 – это множество пар таких что
– это множество пар таких что 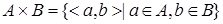 . Бинарным отношением f из множества А в множество В называется подмножество
. Бинарным отношением f из множества А в множество В называется подмножество 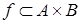 .
.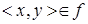 и
и 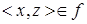 следует, что x = z, то есть функциональность – это однозначность.
следует, что x = z, то есть функциональность – это однозначность.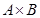 ={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, ….,<4,16>,…..<5,25>}
={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, ….,<4,16>,…..<5,25>}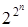 .
. x1 x2 x3 x4
x1 x2 x3 x4 0 0 1 0 0 1 0 0
0 0 1 0 0 1 0 0 )= 1
)= 1


