
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 4. Булевая алгебра. Алгебра логикиСодержание книги Поиск на нашем сайте
Лекция 4. Булевая алгебра. Алгебра логики План лекции 4.1. Понятие высказывания. Простое и составное высказывание 4.2. Логические выражения и логические операции над высказываниями 4.3. Равносильность логических операций. 4.4. Формулы алгебры логики. Функции алгебры логики 4.5. Формы представления высказываний 4.6. Полнота системы булевых функций 4.7. Минимизация высказываний методом Квайна Понятие высказывания. Простое и составное высказывание
Рассмотрим логику высказываний. Логика высказываний строится также, как и другие математические теории. В качестве основных понятий берется некоторый класс объектов, а также некоторые свойства, отношения и операции над этими объектами. Основным объектом логики высказываний служат простые высказывания. Определение. Высказывание — это повествовательное предложение, выражающее суждение. Если суждение, составляющее содержание (смысл) некоторого высказывания, истинно, то и о данном высказывании говорят, что оно истинно. В противном случае, если суждение, составляющее содержание некоторого высказывания, ложно, то и о данном высказывании говорят, что оно ложно. Истинность и ложность называются логическими, или истинностными, значениями высказываний. ПРИМЕРЫ. 1. Число 100 делится на 5. (Истина) 2. Число 3 больше числа 5. (Ложь) 3. Сегодня светит солнце. (Не является высказыванием) 4. Вечером мы пойдем в кино. (Не является высказыванием) 5. Я лгу. (Не является высказыванием) В алгебре высказываний не рассматривают внутреннюю структуру и содержание высказываний, а ограничиваются рассмотрением их свойства, которое представляет истину или ложь. Из высказываний путем соединения их различными способами можно составлять новые, более сложные высказывания. Для образования таких комбинаций будем использовать логические операции, основные из которых вводятся следующим образом.
Формы представления высказываний Полином Жегалкина Пусть M – некоторое произвольное подмножество булевого куба Определение. Формула вида где суммирование ведется по модулю два, а коэффициенты
Если суммирование в формуле (4.1) ведется по всем булевым векторам длины n, слагаемые идут в порядке возрастания номеров булевых векторов и Теорема 4.3. Каждая булева функция от n переменных может быть реализована в виде канонического полинома Жегалкина от n переменных, причем единственным образом. Например, полином Жегалкина от двух переменных Для представления булевой функции в форме полинома Жегалкина воспользуемся треугольником Паскаля. ПРИМЕР. Построим полином Жегалкина для функции f = (10011110). Полином Жегалкина можно получить с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответствует набору (101). В качестве слагаемого многочлена берем x 1 x 3. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
Тогда
Лекция 4. Булевая алгебра. Алгебра логики План лекции 4.1. Понятие высказывания. Простое и составное высказывание 4.2. Логические выражения и логические операции над высказываниями 4.3. Равносильность логических операций. 4.4. Формулы алгебры логики. Функции алгебры логики 4.5. Формы представления высказываний 4.6. Полнота системы булевых функций 4.7. Минимизация высказываний методом Квайна
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.49.59 (0.009 с.) |

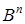 ,
, 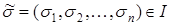 ,
, 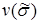 – номер вектора
– номер вектора 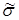 ,
, 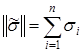 – его вес,
– его вес, 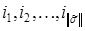 – номера отличных от нуля координат вектора
– номера отличных от нуля координат вектора 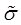 .
.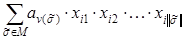 , (4.1)
, (4.1)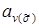 равны либо 0, либо 1, называется полиномом Жегалкина от n переменных.
равны либо 0, либо 1, называется полиномом Жегалкина от n переменных.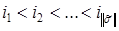 , то говорят, что полином Жегалкина записан в канонической форме.
, то говорят, что полином Жегалкина записан в канонической форме.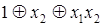 в канонической форме запишется так:
в канонической форме запишется так: 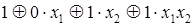 .
.



