
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совершенные нормальные формы сднф, скнф
Определение. СДНФ (совершенная ДНФ) – это такая ДНФ, в которой каждая элементарная конъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные конъюнкции не повторяются. ПРИМЕР.
Определение. СКНФ (совершенная КНФ) – это такая КНФ, в которой каждая элементарная дизъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные дизъюнкции не повторяются. ПРИМЕР.
Каждая формула имеет одну единственную СДНФ и одну единственную СКНФ. Тавтология не имеет СКНФ, а противоречие – СДНФ. Как известно, каждая формула логики высказываний представляет некоторую булеву функцию. Возникает обратный вопрос: можно ли всякую булеву функцию представить некоторой формулой логики высказываний? Можно указать алгоритм, который позволяет по таблице истинности произвольной булевой функции от любого числа переменных построить некоторую формулу логики высказываний в СДНФ. Если рассматривать произвольную функцию, то необходимо выделить все наборы переменных, для которых функция принимает значение 1 и каждому набору поставить в соответствие конъюнкцию переменных и их отрицаний. Рассматриваемая функция будет представлена дизъюнкцией этих конъюнкций. Таким образом, установлена процедура, которая позволяет для всякой булевой функции записать соответствующую ей формулу. ПРИМЕР.
Также для построения СДНФ и СКНФ используется семантическое дерево. ПРИМЕР. Построить СДНФ и СКНФ функции заданной своим семантическим деревом.
Так как СДНФ сохраняет 1, то будем рассматривать листы на которых изображены 1. Листья просматриваются слева направо. Путь от корня дерева к первому листу с единицей определяет конституенту единицы Дизъюнкция конституент единицы образует СДНФ Для того чтобы построить СКНФ будет рассматривать листья на которых изображен 0, так как СКНФ сохраняет 0, Снова просматривает листья слева направо. Путь от корня дерева к первому листу с нулем определяет конституенту нуля
Конъюнкция конституент нуля образует СКНФ
Полином Жегалкина Пусть M – некоторое произвольное подмножество булевого куба Определение. Формула вида где суммирование ведется по модулю два, а коэффициенты Если суммирование в формуле (4.1) ведется по всем булевым векторам длины n, слагаемые идут в порядке возрастания номеров булевых векторов и Теорема 4.3. Каждая булева функция от n переменных может быть реализована в виде канонического полинома Жегалкина от n переменных, причем единственным образом. Например, полином Жегалкина от двух переменных Для представления булевой функции в форме полинома Жегалкина воспользуемся треугольником Паскаля. ПРИМЕР. Построим полином Жегалкина для функции f = (10011110). Полином Жегалкина можно получить с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответствует набору (101). В качестве слагаемого многочлена берем x 1 x 3. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
Тогда
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.38.117 (0.008 с.) |

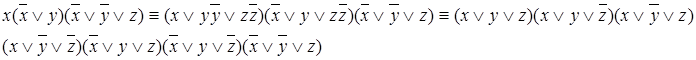
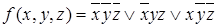

 , это соответствует значению функции F (0,1, c). Путь от корня дерева ко второму листу с единицей определяет конституенту единицы
, это соответствует значению функции F (0,1, c). Путь от корня дерева ко второму листу с единицей определяет конституенту единицы  . Путь от корня дерева к третьему листу с единицей определяет конституенту единицы
. Путь от корня дерева к третьему листу с единицей определяет конституенту единицы  . Путь от корня дерева к четвертому листу с единицей определяет конституенту единицы
. Путь от корня дерева к четвертому листу с единицей определяет конституенту единицы 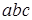 .
.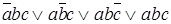 .
. Путь от корня дерева ко второму листу с нулем определяет конституенту нуля
Путь от корня дерева ко второму листу с нулем определяет конституенту нуля 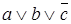 Путь от корня дерева к третьему листу с нулем определяет конституенту нуля
Путь от корня дерева к третьему листу с нулем определяет конституенту нуля 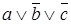 Путь от корня дерева к четвертому листу с нулем определяет конституенту нуля
Путь от корня дерева к четвертому листу с нулем определяет конституенту нуля 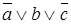 .
.
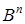 ,
, 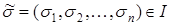 ,
, 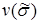 – номер вектора
– номер вектора 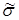 ,
, 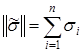 – его вес,
– его вес, 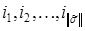 – номера отличных от нуля координат вектора
– номера отличных от нуля координат вектора 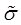 .
.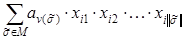 , (4.1)
, (4.1)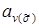 равны либо 0, либо 1, называется полиномом Жегалкина от n переменных.
равны либо 0, либо 1, называется полиномом Жегалкина от n переменных.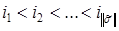 , то говорят, что полином Жегалкина записан в канонической форме.
, то говорят, что полином Жегалкина записан в канонической форме.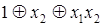 в канонической форме запишется так:
в канонической форме запишется так: 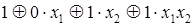 .
.



