
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории автоматического управленияСодержание книги Поиск на нашем сайте
Устойчивость автоматических Систем управления
Понятие об устойчивости. Устойчивость – это свойство системы возвращаться в исходный установившийся режим после нанесения возмущения. На рис. 22 пока-заны типичные кривые переходных процессов в неустойчивой и устойчивой систе-мах.
Рис. 22. Переходные процессы: a – неустойчивые; b – устойчивые.
Процесс регулирования в линейной САУ описывается решением дифференци-ального уравнения системы при известных входных воздействиях и заданных на-чальных условиях аn = b m
Уравнение, у которого правая часть равна нулю, называется однородным, уравнение с ненулевой правой частью – неоднородным. Решение уравнения (2.96) имеет две составляющие y (t) = y
где y Система будет т.е. если с течением времени y Решение однородного дифференциального уравнения
a имеет вид y
где c p
a
Таким образом, переходный процесс y В общем случае корни p
p
В решении дифференциального уравнения системы, описывающем переходный процесс, вещественному корню соответствует слагаемое
D
а паре комплексно–сопряжённых корней – слагаемое
D
Процесс может быть устойчивым лишь при условии, что все его составляющие с течением времени стремятся к нулю. Устойчивость процесса определяется фун-кцией e
p p
Наличие пары сопряжённых чисто мнимых корней p Таким образом, исследование устойчивости системы сводится к определению знаков действительных частей корней. Однако определение корней уравнений вы-ше четвёртой степени связано со сложными расчётами. Поэтому разработан ряд оценок, именуемых критериями устойчивости, по которым можно судить об ус-тойчивости, не решая уравнения. Критерий устойчивости Рауса – Гурвица. Это алгебраический критерий, по которому условие устойчивости сводится к выполнению ряда неравенств, связыва-ющих коэффициенты уравнения системы. В разной форме этот критерий был пред-ложен английским математиком Е. Раусом и затем швейцарским математиком А. Гурвицем. Пусть характеристическое уравнение системы имеет вид
a
Составим из коэффициентов этого уравнения определитель
Этот определитель называется определителем А. Гурвица. Порядок его состав-ления: выписываются по главной диагонали все коэффициенты от a САУ устойчива, если определитель А. Гурвица и все его диагональные миноры положительны. Условие устойчивости: для системы первого порядка – a для системы второго порядка – a для системы третьего порядка – a В общем случае необходимым, но недостаточным условием устойчивости являя-ется положительность всех коэффициентов уравнения. Лишь для систем первого и второго порядков это условие является и достаточным. Использование критерия Рауса – Гурвица для систем высокого порядка (n Критерий устойчивости Михайлова. Этот частотный критерий, предложен-ный русским учёным А.В. Михайловым в 1938 г., основан на изучении годографа вектора комплексной функции, полученной из характеристического многочлена САУ D(p) = a
Подставив p = j
D(j
Здесь U ( САУ устойчива, если годограф Михайлова, начинаясь на действительной поло-жительной полуоси, огибает против часовой стрелки начло координат, проходя последовательно n квадратов (где n – порядок системы). Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат. На рис. 23 приведены годографы Михайлова, соответствующие устойчивой 1, неустойчивой 2 и находящиеся на границе устойчивости 3 САУ четвёртого порядка.
Рис. 23. Годографы Михайлова Рис. 24. АФЧХ разомкнутых САУ
Критерий устойчивости Найквиста. Этот критерий, предложенный в 1932 г. американским учёным Г. Найквистом, позволяет судить об устойчивости замкну-той системы по АФЧХ разомкнутой системы. САУ будет устойчива в замкнутом состоянии, если амплитудно-фазовая характе-ристика разомкнутой системы не охватывает точку с координатами (-1; j0) при из-менении частоты в пределах 0
Систем управления
Требования к промышленным САУ. Задачей промышленной САУ является поддержание оптимального технологического режима в объекте управления. Заданные значения стабилизируемых технологических величин могут изменяться вручную или с помощью управляющей вычислительной машины (УВМ). Возмущающие воздействия в промышленных САУ – изменение режимов работы агрегатов, изменение характеристик материальных и энергетических потоков и т.п. Синтез САУ ставит своей целью обеспечение заданных показателей качества регу-лирования при возмущениях заданного вида. Одной из задач при синтезе САУ яв-ляется определение значений параметров настройки регуляторов. Расчёт регулято-ров производится исходя из требования обеспечения оптимального качества регу-лирования. Показатели качества регулирования. Устойчивость является необходимым условием работоспособности САУ, но недостаточным с точки зрения качества ре-гулирования. Ниже перечислены прямые показатели качества регулирования (рис. 25): t
Рис. 25. Показатели качества регулирования.
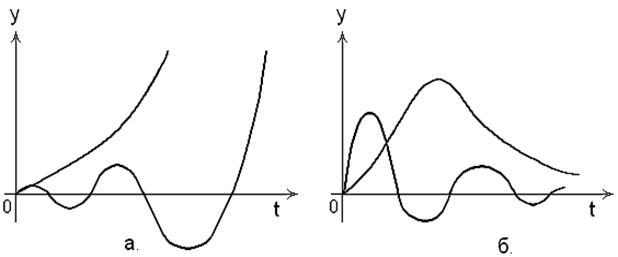
Косвенными показателями качества регулирования являются Оптимальные переходные процессы. На основании опытов и теоретических обобщений для промышленных объектов рекомендован ряд оптимальных переходных процессов регулирования (рис.26).
Рис. 26. Оптимальные переходные процессы: a. – апериодический; б. – с 20% - ным перерегулированием; в. – с минимальной квадратичной площадью.
1. Апериодический переходный процесс – характеризуется минимальным време-нем регулирования, отсутствием перерегулирования и максимальным динамичес-ким отклонением. 2. Затухающий колебательный переходный процесс с 20 %-ным перерегулирова-нием – характеризуется минимальным динамическим отклонением и временем первого полупериода колебаний t 3. Затухающий колебательный переходный процесс с минимальной квадратичной площадью I характеризуется 40-45 %-ным перерегулированием и максимальным временем ре-гулирования; имеет наименьшее динамическое отклонение. Типы регуляторов. По характеру действия регуляторы бывают релейные, им-пульсные и непрерывные. Релейные (позиционные) регуляторыосуществляют ступенчатое управляющее воздействие. Наиболее распространены двухпозиционные регуляторы. В этом слу-чае регулирующий орган может принимать одно из двух предельных положений: открыто или закрыто. Импульсные регуляторы имеют в своей структуре импульсное звено и коммути-рующее устройство. Регулятор позволяет управлять одним или несколькими инер-ционными объектами, так как изменение регулирующего воздействия носит дис-кретный характер. Непрерывные промышленные регуляторы в зависимости от реализуемого закона регулирования бывают пропорциональные, пропорционально-интегральные и пропорционально-интегрально-дифференциальные. Пропорциональный регулятор (П-регулятор) производит перемещение регули-рующего органа пропорционально отклонению регулируемой величины от задан-ного значения. Уравнение П – регулятор y = K где K Передаточная функция П – регулятора W (p) = K
Амплитудно-фазовая и переходная характеристики W (j
h (t) = K
Недостатком П – регуляторов является зависимость регулируемой величины от нагрузки. Это явление называется остаточной неравномерностью регулирования (статической ошибкой). Параметром настройки П – регулятора служит диапазон дросселирования, рав-ный
Пропорционально-интегральный регулятор (ПИ – регулятор) производит пере-мещение регулирующего органа пропорционально сумме отклонения и интеграла от отклонения регулируемой величины. Уравнение ПИ – регулятора y = K
где KР – коэффициент усиления регулятора; TИ – время изодрома (интегрирования). При TИ Передаточная функция, амплитудно-фазовая и переходная характеристики ПИ – регулятора равны W(p) = K W(j h(t) = K Переходная характеристика ПИ – регулятора приведена на рис. 27. За время t = TИ интегральная составляющая становится равной пропорциональной, т.е. сиг-нал удваивается. Поэтому время изодрома называют временем удвоения. Так как интегральная составляющая вводится воздействием на упругую обратную связь (изодром), то ПИ – регуляторы называются изодромными. Параметры настройки ПИ – регулятора: диапазон дросселирования Пропорционально-интегрально-дифференциальный регулятор (ПИД – регулятор) производит перемещение регулирующего органа пропорционально отклонению, интегралу и скорости изменения регулируемой величины. Уравнение ПИД – регулятора
y = K Р (x +
где KР – коэффициент усиления регулятора; TДИФ – время дифференцирования. При TДИФ = 0 ПИД – регулятор превращается в ПИ – регулятор.
Рис. 27. Переходная характеристика ПИ – регулятора. Рис. 28. Переходная характеристика ПИД – регулятра.
Передаточная функция ПИД – регулятора
W (p) = K Р (1 +
Амплитудно-фазовая характеристика
W (j
Переходная характеристика H (t) = H (t) = KР (1+
График переходной характеристики ПИД – регулятора приведён на рис. 28. Параметры настройки ПИД – регулятора: диапазон дросселирования Исходные данные для расчёта автоматического регулятора. Для расчёта автоматического регулятора непрерывного действия необходимо иметь следующие исходные данные: динамические характеристики объекта – постоянная времени T, c; запазды-вание максимально возможное возмущение по нагрузке – требуемые показатели качества регулирования – максимально допустимое динамическое отклонение A Расчёт регулятора сводится к выбору типа регулятора и определению оптималь-ных параметров настройки. Выбор типа автоматического регулятора. Расчёт промышленных САУ может быть проведён различными методами: аналитическим, математического моделиро-вания на ЭВМ, графоаналитическим и экспериментально. Общедоступным является графоаналитический метод, достоинствами которого являются его простота и достаточная точность результатов. Сущность этого метода состоит в том, что расчёт регулятора производится по заранее составленным графи-кам с учётом динамических свойств САУ и требований к качеству переходного процесса. При выборе типа регулятора следует прежде всего определить характер действия регулятора. Такой выбор ориентировочно может быть сделан, исходя из величины отношения запаздывания Выбор типа регулятора производится по величине динамического коэффициента регулирования, определяемого по формуле
KДИН =
Имея численное значение KДИН и задаваясь типом оптимального переходного процесса, по графикам функциональной зависимости KДИН от
Рис. 29. Графики выбора типа регулятора
Выбранный тип регулятора далее проверяется на соответствие фактического вре-мени регулирования заданному и фактического остаточного отклонения регулиру-емой величины заданному значению (последнее только для П-регуляторов). Такие проверки осуществляются по специальным графикам. Определение оптимальных параметров настройки регулятора. К промышленным САУ предъявляются следующие требования: система должна обладать заданным запасом устойчивости; динамическая ошибка, величина перерегулирования и ста-тическая ошибка е должны быть больше заданных; время регулирования должно быть минимальным. Выполнение двух последних требований возможно при мини-мизации одного из указанных из указанных ниже интегральных критериев
I 1 = Большинство методов определения оптимальных параметров настройки регуля-торов предусматривает решение задачи в два этапа: 1. Определение области, соответствующей заданному запасу устойчивости. В ка-честве критерия оптимальности на этом этапе обычно используют показатель коле-бательности M =
где |W(j Обычно считается, что система обладает необходимым запасом устойчивости, если М = 1,62 2. Определение в выделенной области оптимальных параметров настроек. В ка-честве критерия оптимальности на этом этапе используются интегральные крите-рии I 1 и I 2. Для объектов высокого порядка расчёт регуляторов сопровождается сложными вычислениями. Для объектов первого порядка с запаздыванием расчёт может быть проведён с помощью специальных таблиц (табл. 2.1) или по графикам.
Управления
Автоматическая система регулирования, в состав которой включены звенья, име-ющие нелинейную статическую характеристику, называется нелинейной. В данном случае речь идёт о существенно нелинейных звеньях, статические характеристики которых не могут быть линеаризованы известными методами без потери их су-щественных особенностей. В настоящее время из всего многообразия нелинейных характеристик выделен класс существенно нелинейных, которые могут быть отне-сены к типичным нелинейностям. Такие характеристики включают зоны нечувст-вительности, насыщения, гистерезиса и т.п. Существенно нелинейными могут быть характеристики различных звеньев системы регулирования: датчиков, исполни-тельных механизмов, регуляторов. Широкое применение в автоматизации произ-водственных процессов получили нелинейные системы регулирования с регулято-рами, имеющими релейную статическую характеристику. Это так называемые сис-темы позиционного регулирования. Сигнал на выходе позиционного регулятора в зависимости от величины входного сигнала может принимать одно из двух возможных постоянных значений ymax или ymin. Последнее в частном случае может равняться нулю. На рис.32 приведена релейная характеристика.
Рис. 32. Статистическая характеристика позиционного регулятора.
При достижении входным сигналом величины порога срабатывания В качестве примера рассмотрим работу автоматической системы регулирования уровня жидкости в ёмкости с позиционным регулятором ПР 1.6, функциональная и структурная схемы которой показаны на рис.33.
Рис. 33. Автоматическая система регулиированияуровня С позиционным регулятором: а. – функциональная схема; б. – структурная схема.
Проиллюстрируем работу системы регулирования графиками. Когда уровень жидкости в ёмкости в результате стока упадёт ниже заданного значения
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.195.127 (0.012 с.) |

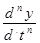 + an-1
+ an-1 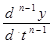 + … + a
+ … + a 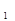
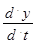 + a
+ a 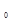 y =
y =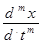 + b m-1
+ b m-1 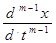 … + b
… + b 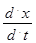 + b
+ b 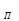 (t) + y
(t) + y 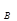 (t) (2.97)
(t) (2.97) устойчивая, если переходные процессы y
устойчивая, если переходные процессы y 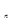
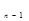
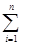 c
c 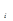 e
e 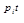 , (2.99)
, (2.99)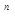 + a
+ a 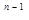 + … + a
+ … + a 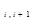 =
= 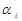
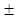 j
j  . (2.101)
. (2.101)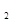 = c
= c 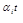 , (2.102)
, (2.102)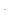 (c
(c 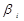
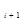
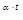 . Для устойчивости линейной системы необходимо, чтобы все вещест-венные корни и вещественные части комплексных корней были отрицательны
. Для устойчивости линейной системы необходимо, чтобы все вещест-венные корни и вещественные части комплексных корней были отрицательны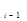 = –
= – 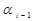 ; (2.104)
; (2.104)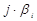 . (2.105)
. (2.105)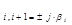 даёт незатуха-ющую гармоническую составляющую переходного процесса. В этом случае систе-ма находится на границе устойчивости. Такая система так же неработоспособна, как и неустойчивая.
даёт незатуха-ющую гармоническую составляющую переходного процесса. В этом случае систе-ма находится на границе устойчивости. Такая система так же неработоспособна, как и неустойчивая.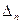 =
= 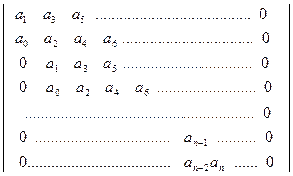 (2.107)
(2.107)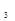 a
a 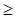 4) становится трудным в связи с увеличением объёма вычислений. ========================
4) становится трудным в связи с увеличением объёма вычислений. ========================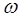 , получаем комплексную функцию
, получаем комплексную функцию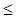
 , получим ряд значений вектора D (j
, получим ряд значений вектора D (j 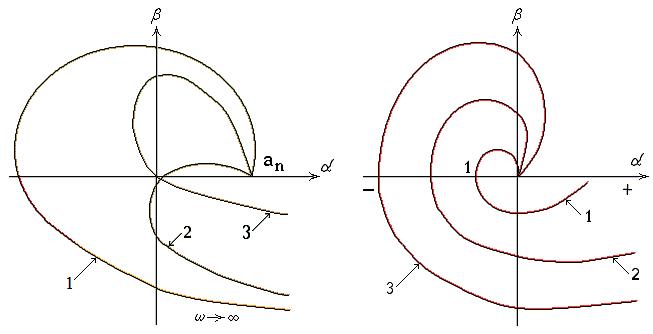
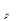 – время регулирования, в течение которого регулируемая величина до-стигает заданного значения; x
– время регулирования, в течение которого регулируемая величина до-стигает заданного значения; x 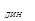 – динамическая ошибка, т.е. максимальное от-клонение регулируемой величины в переходном процессе; x
– динамическая ошибка, т.е. максимальное от-клонение регулируемой величины в переходном процессе; x 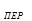 – величина пере-регулирования;
– величина пере-регулирования; 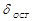 – статическая ошибка, т.е. остаточное отклонение регулируе-мой величины после окончания переходного процесса (имеет место только в стати-ческих САУ). Перечисленные показатели могут быть определены непосредственно по графику переходного процесса и поэтому называются прямыми.
– статическая ошибка, т.е. остаточное отклонение регулируе-мой величины после окончания переходного процесса (имеет место только в стати-ческих САУ). Перечисленные показатели могут быть определены непосредственно по графику переходного процесса и поэтому называются прямыми.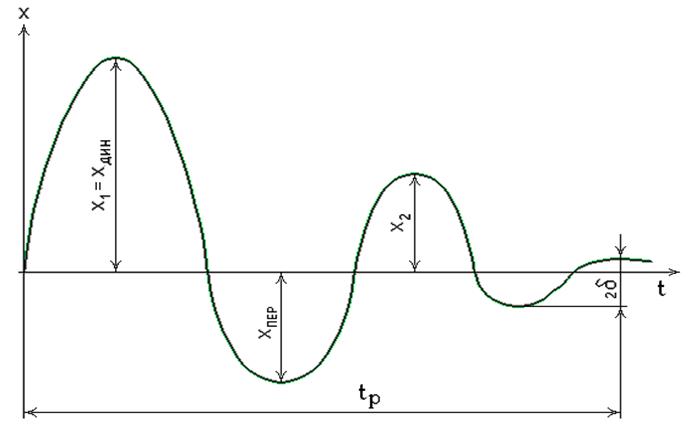
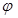 =
= 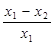 – сте-пень затухания, характеризующая колебательность процесса; I
– сте-пень затухания, характеризующая колебательность процесса; I 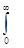 x (t) dt – простейшая интегральная оценка (качество регулирования оценивается по величине площади, заключённой между кривой переходного процесса и осями координат), используемая для переходных процессов, не имеющих перерегулирования; I
x (t) dt – простейшая интегральная оценка (качество регулирования оценивается по величине площади, заключённой между кривой переходного процесса и осями координат), используемая для переходных процессов, не имеющих перерегулирования; I 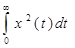 – квадратичная интегральная оценка, используемая для оценки любых процессов регулирования.
– квадратичная интегральная оценка, используемая для оценки любых процессов регулирования.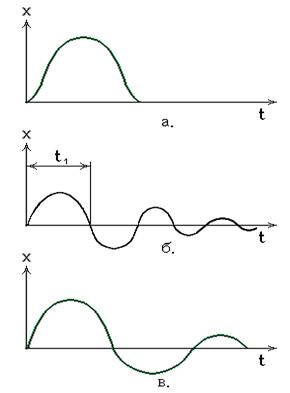
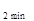 =
= 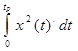 –
–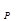 x, (2.110)
x, (2.110)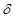 =
= 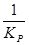
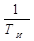
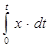 ), (2.115)
), (2.115)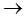
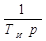 ); (2.116)
); (2.116)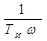 ); (2.117)
); (2.117)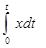 + T ДИФ
+ T ДИФ 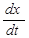 ) (2.119)
) (2.119)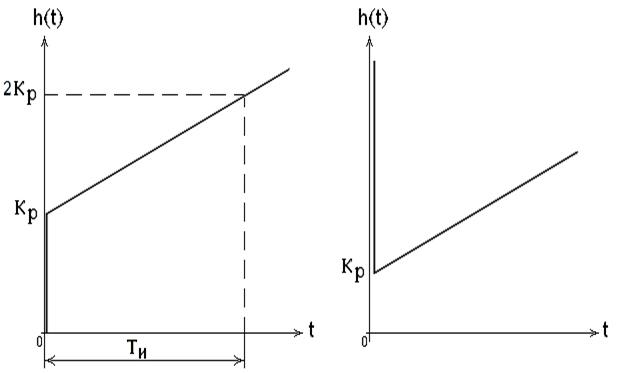
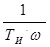 + j
+ j 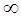 при t =0,
при t =0,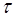 , с; коэффициент усиления KОБ.
, с; коэффициент усиления KОБ.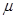 ;
;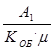 . (2.123)
. (2.123)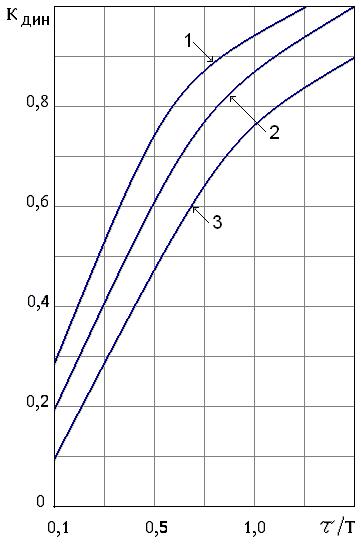
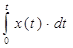 ; I 2 =
; I 2 = 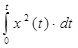 .
.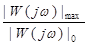 , (2.124)
, (2.124)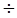 1,29;
1,29;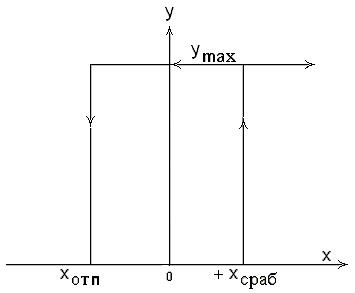
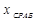 вы-ходной сигнал изменяется скачкообразно от минимального
вы-ходной сигнал изменяется скачкообразно от минимального 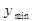 до максимального
до максимального 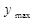 значения. При дальнейшем увеличении входного сигнала выходная величина не изменяется, сохраняя своё максимальное значение
значения. При дальнейшем увеличении входного сигнала выходная величина не изменяется, сохраняя своё максимальное значение 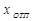 выходной сигнал уменьшится скачком до минимальной величины
выходной сигнал уменьшится скачком до минимальной величины 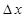 =
= 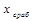 -
- 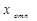 назы-вают зоной неоднозначности. Характеристику, подобную изображённой на рис.32, имеет позиционный пневматический регулятор системы «Старт» ПР 1.5. Последняя модификация этого регулятора ПР 1.6 позволяла изменять величину зоны неод-нозначности.
назы-вают зоной неоднозначности. Характеристику, подобную изображённой на рис.32, имеет позиционный пневматический регулятор системы «Старт» ПР 1.5. Последняя модификация этого регулятора ПР 1.6 позволяла изменять величину зоны неод-нозначности.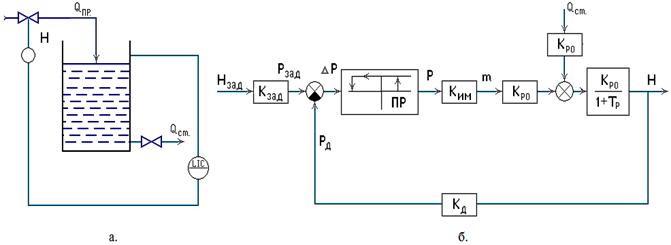
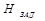 и ве-личина ошибки регулирования
и ве-личина ошибки регулирования 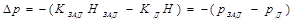 достигает зна-чения
достигает зна-чения 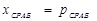 , где
, где 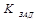 – коэффициент усиления задающего устройства, сиг-нал на выходе регулятора примет в соответствии с его статической характеристи-кой своё максимальное значение
– коэффициент усиления задающего устройства, сиг-нал на выходе регулятора примет в соответствии с его статической характеристи-кой своё максимальное значение 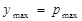 . В результате этого клапан подачи жид-кости в ёмкость полностью откроется и расход жидкости на входе в ёмкость до-стигнет своего максимального значения
. В результате этого клапан подачи жид-кости в ёмкость полностью откроется и расход жидкости на входе в ёмкость до-стигнет своего максимального значения 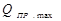 . Так как максимальное значение расхода на притоке
. Так как максимальное значение расхода на притоке 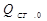 , то уровень будет возрастать и к моменту времени
, то уровень будет возрастать и к моменту времени 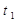 превысит заданное значение. При этом сигнал на входе регулятора достигнет порога отпускания
превысит заданное значение. При этом сигнал на входе регулятора достигнет порога отпускания 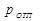 . В соответствии со статической характеристикой регулятора сигнал на его выходе примет своё минимальное значение
. В соответствии со статической характеристикой регулятора сигнал на его выходе примет своё минимальное значение 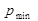 = 0. Это приведёт к закрытию клапана подачи на притоке и к ум
= 0. Это приведёт к закрытию клапана подачи на притоке и к ум


