Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Позиционные системы счисления. ⇐ ПредыдущаяСтр 5 из 5
В позиционных системах счисления для записи чисел используется некоторое количество отличных друг от друга знаков - цифр. Их число является основанием системы счисления. В позиционной системе счисления число может быть представлено в виде суммы произведений коэффициентов на соответствующие степени основания системы. Например, в привычной нам десятичной системе используется десять цифр – 0,1,...,9, и число записанное с их помощью, может быть подсчитано по формуле:
Здесь запятая отделяет целую часть от дробной, умножение обозначается «х», сложение «+», действия выполняются по правилам десятичной системы. Значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа (поэтому такие системы и называются позиционными). Общая формула для систем с любым основанием выглядит так:
Здесь l – основание системы счисления (целое положительное число, не меньшее 2); в левой части формулы – формальная запись числа в l – ной системе счисления; справа – формула для подсчета реального значения числа. Если основание системы счисления меньше 10, то используется нужное количество привычных цифр, а если больше 11 – к цифрам добавляются буквы. Так, общепринятая база двенадцатиричной системы счисления: 0,1,2,3,4,5,6,7,8,9,А,В; а шестнадцатеричной – 0,1,2,3,4,5,6,7,8,9,А,В,С, D,E,F. При этом буква А соответствует цифре 10, В – 11 и т.д. В каждой системе счисления есть своя таблица сложения и умножения. Для десятичной системы – привычные правила сложения цифр и таблица Пифагора, для остальных систем эти таблицы строятся аналогично. Существуют правила перевода чисел из одной системы в другую. Перевод числа из системы с произвольным основанием в десятичную дается формулой (4). Перевод числа из десятичной системы в систему с произвольным основанием l осуществляется раздельно для целой и дробной части. Чтобы перевести целую часть необходимо разделить ее на l. Остаток даст младший разряд, записанный в l - цифрах. Полученное частное опять делим на l – новый остаток даст следующий разряд, и т.д. Процесс останавливается, когда частное станет равным нулю. Полученный при этом остаток дает старший разряд числа. Для перевода дробной части числа ее необходимо умножить на l. Целая часть полученного произведения (в l – цифрах) будет первым после запятой знаком. Дробную часть полученного произведения опять умножаем на основание и выделяем следующую цифру, и т.д. Процесс останавливается, когда дробная часть произведения обратиться в ноль, или когда будет достигнута требуемая точность. Отметим, что конечная дробь в одной системе счисления может превратиться в бесконечную дробь в другой (под дробью здесь понимаются аналоги десятичных дробей).
Кроме позиционных систем счисления существуют такие, в которых значение знака не зависит от того места, которое он занимает в записи числа. Такие системы называются непозиционными, и примером такой системы является римская. В этой системе используется 7 знаков: I –1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000. Запись числа представляет собой перечисление ряда из этих символов, а значение числа подсчитывается суммированием значений всех записанных символов. Например: III – 1+1+1=3; DCCLXXVII – 500+100+100+50+10+10+5+1+1= 777. Недостатком таких систем, из-за которых они имеют лишь ограниченное декоративное применение, является отсутствие формальных правил записи чисел и, соответственно, правил действий над ними. Двоичная система счисления. Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описывается наборами только из двух знаков – 0 и 1. Покажем пример перевода чисел из десятичной системы счисления в двоичную и обратно:
Число 28,73 требуется перевести в двоичную систему с точностью 4 знака после запятой. Целая и дробная части переводятся отдельно. Все действия проводятся в десятичной системе. Целая часть: Частное Остаток 28:2=14 0 14:2=7 0 7:2=3 1 3:2=1 1 1:2=0 1 Т. о. 2810=111002. Дробная часть: Произведение Целая часть 0,73*2= 1,46 1 0,46*2= 0,92 0 0,92*2= 1,84 1 0,84*2= 1,68 1 ... Т. о. 0,7310=0,1011...2. В итоге 28,7310=11100,1011...2. Обратный перевод осуществляется по формуле (4):
Отметим тот факт, что конечная десятичная дробь чаще всего не переводится в конечную двоичную дробь. При этом обратный перевод не приводит к исходному результату, и возникает погрешность (см. пример). Однако, если удалось перевести конечную дробь в конечную дробь, то обратный перевод будет точным. Этот факт справедлив для двух любых систем счисления, а не только для десятичной и двоичной.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.193.172 (0.005 с.) |
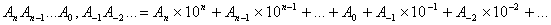 (3)
(3)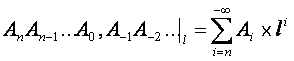 (4)
(4)