
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение количества информацииСодержание книги Поиск на нашем сайте
Определить понятие «количество информации» довольно сложно из-за неопределенности самого понятия «информация». В решении этой проблем известны два подхода – кибернетический (вероятностный) и количественный (объемный). Кибернетический подход. Кибернетический подход сейчас применяется в основном в теории вероятностей и позволяет подсчитать количество информации, которое несет результат какого-то опыта (например, бросания монеты, игральной кости, раунд в рулетке и т.д.). Этот подход был развит в конце 40-х годов XXвека математиками Хартли и Шенноном. Основные полученные ими результаты заключаются в следующем: a) если какой-то опыт может иметь N равновероятных исходов, количество информации, появляющейся после его однократного проведения, вычисляется по формуле Хартли:
b) При введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Из формулы (1) следует, что H=1 при N=2. Иначе говоря, в качестве единицы измерения принимается количество информации, связанное с однократным проведением опыта, состоящего в получении одного из двух равновероятных исходов. Результаты исходов обозначаются двоичными цифрами 0 и 1, а единица информации называется «бит» (от англ. BInary digiTs – двоичные цифры). c) Если проводится опыт с исходами, вероятности появления которых различны, то количество информации определяется формулой Шеннона:
Здесь N – количество исходов опыта, Pi – вероятность каждого исхода. Если проводится несколько независимых опытов, суммарное количество полученной информации равно сумме количеств информации, полученной после каждого из опытов. Например, определим количество информации, связанное с появлением каждого символа в сообщении, записанном русскими буквами. Русский алфавит (упрощенно) состоит из 33 букв и пробела, и, по формуле (1), Объемный подход. Объемный подход измерения количества информации возник вместе с ЭВМ. Создателям компьютеров потребовался научный подход, допускающий не просто измерение количества информации, но и предлагающий способы ее преобразования, передачи и хранения. Вся информация в компьютере хранится, передается и обрабатывается в виде двоичных кодов – последовательностей двоичных цифр 0 и 1. Двоичная система выбрана потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния – есть ток / нет тока, направление намагниченности и т.д. В компьютере бит является наименьшей возможной единицей информации. Доказано, что любая дискретная информация может быть представлена последовательностью битов (это вопрос из раздела кодирования), а, так как мы уже знаем о возможности дискретизации непрерывной информации с любой степенью точности, то можно считать, что любая информация может быть представлена последовательностью битов с любой степенью точности. Суммарный объем какой-либо информации подсчитывается просто по количеству требуемых для такой записи битов. При этом, очевидно, невозможно нецелое число битов, в отличие от вероятностного подхода. Для удобства использования введены и более крупные единицы: 1 байт = 8 бит 1 килобайт (кБ) = 1024 байт 1 мегабайт (МБ) = 1024 кБ 1 гигабайт (ГБ) = 1024МБ.
Между вероятностным и объемным подходом существует весьма неоднозначное соответствие. Не всякий текст, даже записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает в объемном. Даже если некоторое сообщение допускает измерение количества в обоих смыслах, то результаты измерений далеко не всегда совпадают. Но, при этом, кибернетическое количество одной и той же информации не может быть больше объемного.
КОДИРОВАНИЕ ИНФОРМАЦИИ Формирование представления информации называется ее кодированием. В более узком смысле под кодированием понимается переход от исходного представления информации, удобного для восприятия информации человеком, к представлению, удобному для хранения, передачи и обработки. В этом случае обратный переход к исходному представлению называется декодированием. При кодировании информации ставятся следующие цели: · удобство физической реализации; удобство восприятия; · высокая скорость передачи и обработки; · экономичность, т.е. уменьшение избыточности сообщения; · надежность, т.е. защита от случайных искажений; · сохранность, т.е. защита от нежелательного доступа к информации. Поскольку информация представляется в компьютере последовательностью двоичных цифр, для понимания процессов обработки и кодирования информации необходимо познакомиться с математическими основами теории систем счисления, в частности, двоичной, восьмеричной и шестнадцатеричной. СИСТЕМЫ СЧИСЛЕНИЯ Система счисления – принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса – позиционные и непозиционные. В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая - 7 единиц, а третья - 7 десятых долей единицы. Сама же запись числа 757,7 означает сокращенную запись выражения 700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7. Любая позиционная система счисления характеризуется своим основанием. Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе.
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.66 (0.008 с.) |

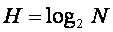 (1)
(1)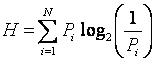 (2)
(2)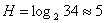 бит. Однако, в русских словах (и в словах других языков) различные буквы встречаются неодинаково часто. Если воспользоваться таблицей частотности букв русского языка и формулой (2), то получится несколько меньший результат: 4,72бит.
бит. Однако, в русских словах (и в словах других языков) различные буквы встречаются неодинаково часто. Если воспользоваться таблицей частотности букв русского языка и формулой (2), то получится несколько меньший результат: 4,72бит.


