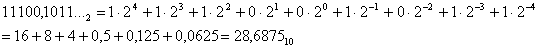Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы информатикиСодержание книги
Поиск на нашем сайте
Теоретические основы информатики 1. ИНФОРМАТИКА КАК НАУКА И КАК ВИД ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ.. 1 1.1. ИСТОРИЯ РАЗВИТИЯ ИНФОРМАТИКИ.. 1 1.2. МЕСТО ИНФОРМАТИКИ В СИСТЕМЕ НАУК. 3 1.3. СОЦИАЛЬНЫЕ АСПЕКТЫ ИНФОРМАТИКИ.. 4 2. ИНФОРМАЦИЯ, ЕЕ ВИДЫ И СВОЙСТВА. 5 2.1. ОБЩЕЕ ПРЕДСТАВЛЕНИЕ ОБ ИНФОРМАЦИИ.. 5 2.2. ИНФОРМАЦИЯ И ФИЗИЧЕСКИЙ МИР. 7 2.3. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ.. 8 3. КОДИРОВАНИЕ ИНФОРМАЦИИ.. 10 3.1. СИСТЕМЫ СЧИСЛЕНИЯ. 10 3.2. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ. 14 В любой науке есть фундамент, без которого невозможно правильное понимание ее прикладных аспектов (пример: математика – теория чисел, теория множеств, мат. логика и др.). Так же и с информатикой – можно изучить насколько программ и даже научиться программировать на каком-то одном языке, но это не вся информатика, не самая главная и интересная ее часть. Теоретическая информатика складывается из ряда разделов математики: теории алгоритмов, теории автоматов, математической логики, теории формальных языков и грамматик, реляционной алгебры, теории информации и др. Теоретическая информатики старается методами точного анализа ответить на вопросы, возникающие при работе с информацией (пример: вопрос о количестве информации, наиболее рациональной организации для хранения и поиска нужной информации и др.). Изучение и понимание теоретических основ информатики является необходимым условием для того, чтобы стать специалистом в этой науке. Другое дело – с какой глубиной изучать. Многие разделы теоретической информатики достаточно сложны и требуют серьезной математической подготовке. Далее они будут рассмотрены скорее в ознакомительном порядке, с целью составить о них отчетливое представление.
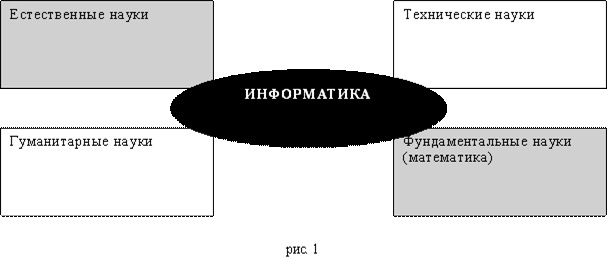
ИНФОРМАТИКА КАК НАУКА И КАК ВИД ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ МЕСТО ИНФОРМАТИКИ В СИСТЕМЕ НАУК Рассмотрим место информатики в традиционной исторически сложившейся системе наук (технических, естественных, гуманитарных и т.д.). По определению акад. А.П. Ершова, информатика – «фундаментальная естественная наука». Академик Б.П. Наумов определил информатику как «естественную науку, изучающую общие свойства информации, процессы, методы и средства ее обработки (сбор, хранение, преобразование, перемещение, выдача)». Уточним, что такое фундаментальная и естественная наука. К фундаментальным относят науки, основные понятия и термины которых носят общенаучный характер, используются во многих других науках и видах деятельности (математика, философия). Несомненно, к фундаментальным наукам относится и информатика, т.к. понятия «информация», «обработка информации» и др. имеют общенаучную значимость. Естественные науки – физика, химия, биология и др. – имеют дело с объективными сущностями мира, имеющими место независимо от нашего сознания. Отнесение к ним информатики отражает единство законов обработки информации в системах самой разной природы – искусственных, биологических, общественных. Информатика имеет характерные черты и других групп наук – технических и гуманитарных (общественных). Черты технической науки придают информатике ее аспекты, связанные с созданием и функционированием систем машинной обработки информации. Академик А.А. Дородницын определяет состав информатики как «три неразрывно связанные части: технические, программные и алгоритмические средства». Но информатики присущи также черты гуманитарной науки, проявляющиеся в ее вкладе в развитие и совершенствование социальной сферы. Таким образом, информатика является комплексной, междисциплинарной отраслью научного знания, стоящей на пересечении разных групп наук (см. рис.1).
ИНФОРМАЦИЯ, ЕЕ ВИДЫ И СВОЙСТВА. ИНФОРМАЦИЯ И ФИЗИЧЕСКИЙ МИР Одной из важнейших черт функционирования современного общества является его информативная оснащенность. В ходе своего развития общество прошло через пять информационных революций. Первая из них была связана с введением языка, вторая – письменности, третья – книгопечатания, четвертая – радиосвязи, пятая - компьютеров. Каждый раз новые информационные технологии поднимали информированность общества на несколько порядков, радикально меняя объем, глубину и доступность знания, а также уровень культуры в целом. Следовательно, информацию следует считать особым видом ресурса. Имеется в виду ресурс как единый запас неких знаний, материальных предметов, а также энергетических, структурных или каких – то иных категорий. Но, в отличие от материальных ресурсов, информационные ресурсы являются (с некоторыми оговорками) неистощимыми и предполагают существенно иные методы воспроизведения и обновления. Перечислим набор основных свойств информации: · запоминаемость; · передаваемость; · преобразуемость; · воспоизводимость; Этих свойств недостаточно для формирования ее меры, так как они относятся к физическому уровню информационных процессов. В то же время, введение принципов и единиц измерения количества информации стало необходимым для развития ЭВМ. Такие принципы были разработаны, и была введена общая международная единица количества информации. Кибернетический подход. Кибернетический подход сейчас применяется в основном в теории вероятностей и позволяет подсчитать количество информации, которое несет результат какого-то опыта (например, бросания монеты, игральной кости, раунд в рулетке и т.д.). Этот подход был развит в конце 40-х годов XXвека математиками Хартли и Шенноном. Основные полученные ими результаты заключаются в следующем: a) если какой-то опыт может иметь N равновероятных исходов, количество информации, появляющейся после его однократного проведения, вычисляется по формуле Хартли:
b) При введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Из формулы (1) следует, что H=1 при N=2. Иначе говоря, в качестве единицы измерения принимается количество информации, связанное с однократным проведением опыта, состоящего в получении одного из двух равновероятных исходов. Результаты исходов обозначаются двоичными цифрами 0 и 1, а единица информации называется «бит» (от англ. BInary digiTs – двоичные цифры). c) Если проводится опыт с исходами, вероятности появления которых различны, то количество информации определяется формулой Шеннона:
Здесь N – количество исходов опыта, Pi – вероятность каждого исхода. Если проводится несколько независимых опытов, суммарное количество полученной информации равно сумме количеств информации, полученной после каждого из опытов. Например, определим количество информации, связанное с появлением каждого символа в сообщении, записанном русскими буквами. Русский алфавит (упрощенно) состоит из 33 букв и пробела, и, по формуле (1), Объемный подход. Объемный подход измерения количества информации возник вместе с ЭВМ. Создателям компьютеров потребовался научный подход, допускающий не просто измерение количества информации, но и предлагающий способы ее преобразования, передачи и хранения. Вся информация в компьютере хранится, передается и обрабатывается в виде двоичных кодов – последовательностей двоичных цифр 0 и 1. Двоичная система выбрана потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния – есть ток / нет тока, направление намагниченности и т.д. В компьютере бит является наименьшей возможной единицей информации. Доказано, что любая дискретная информация может быть представлена последовательностью битов (это вопрос из раздела кодирования), а, так как мы уже знаем о возможности дискретизации непрерывной информации с любой степенью точности, то можно считать, что любая информация может быть представлена последовательностью битов с любой степенью точности. Суммарный объем какой-либо информации подсчитывается просто по количеству требуемых для такой записи битов. При этом, очевидно, невозможно нецелое число битов, в отличие от вероятностного подхода. Для удобства использования введены и более крупные единицы: 1 байт = 8 бит 1 килобайт (кБ) = 1024 байт 1 мегабайт (МБ) = 1024 кБ 1 гигабайт (ГБ) = 1024МБ.
Между вероятностным и объемным подходом существует весьма неоднозначное соответствие. Не всякий текст, даже записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает в объемном. Даже если некоторое сообщение допускает измерение количества в обоих смыслах, то результаты измерений далеко не всегда совпадают. Но, при этом, кибернетическое количество одной и той же информации не может быть больше объемного.
КОДИРОВАНИЕ ИНФОРМАЦИИ Формирование представления информации называется ее кодированием. В более узком смысле под кодированием понимается переход от исходного представления информации, удобного для восприятия информации человеком, к представлению, удобному для хранения, передачи и обработки. В этом случае обратный переход к исходному представлению называется декодированием. При кодировании информации ставятся следующие цели: · удобство физической реализации; удобство восприятия; · высокая скорость передачи и обработки; · экономичность, т.е. уменьшение избыточности сообщения; · надежность, т.е. защита от случайных искажений; · сохранность, т.е. защита от нежелательного доступа к информации. Поскольку информация представляется в компьютере последовательностью двоичных цифр, для понимания процессов обработки и кодирования информации необходимо познакомиться с математическими основами теории систем счисления, в частности, двоичной, восьмеричной и шестнадцатеричной. СИСТЕМЫ СЧИСЛЕНИЯ Система счисления – принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса – позиционные и непозиционные. В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая - 7 единиц, а третья - 7 десятых долей единицы. Сама же запись числа 757,7 означает сокращенную запись выражения 700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7. Любая позиционная система счисления характеризуется своим основанием. Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе.
Двоичная система счисления. Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описывается наборами только из двух знаков – 0 и 1. Покажем пример перевода чисел из десятичной системы счисления в двоичную и обратно:
Число 28,73 требуется перевести в двоичную систему с точностью 4 знака после запятой. Целая и дробная части переводятся отдельно. Все действия проводятся в десятичной системе. Целая часть: Частное Остаток 28:2=14 0 14:2=7 0 7:2=3 1 3:2=1 1 1:2=0 1 Т. о. 2810=111002. Дробная часть: Произведение Целая часть 0,73*2= 1,46 1 0,46*2= 0,92 0 0,92*2= 1,84 1 0,84*2= 1,68 1 ... Т. о. 0,7310=0,1011...2. В итоге 28,7310=11100,1011...2. Обратный перевод осуществляется по формуле (4):
Отметим тот факт, что конечная десятичная дробь чаще всего не переводится в конечную двоичную дробь. При этом обратный перевод не приводит к исходному результату, и возникает погрешность (см. пример). Однако, если удалось перевести конечную дробь в конечную дробь, то обратный перевод будет точным. Этот факт справедлив для двух любых систем счисления, а не только для десятичной и двоичной. Теоретические основы информатики 1. ИНФОРМАТИКА КАК НАУКА И КАК ВИД ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ.. 1 1.1. ИСТОРИЯ РАЗВИТИЯ ИНФОРМАТИКИ.. 1 1.2. МЕСТО ИНФОРМАТИКИ В СИСТЕМЕ НАУК. 3 1.3. СОЦИАЛЬНЫЕ АСПЕКТЫ ИНФОРМАТИКИ.. 4 2. ИНФОРМАЦИЯ, ЕЕ ВИДЫ И СВОЙСТВА. 5 2.1. ОБЩЕЕ ПРЕДСТАВЛЕНИЕ ОБ ИНФОРМАЦИИ.. 5 2.2. ИНФОРМАЦИЯ И ФИЗИЧЕСКИЙ МИР. 7 2.3. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ИНФОРМАЦИИ.. 8 3. КОДИРОВАНИЕ ИНФОРМАЦИИ.. 10 3.1. СИСТЕМЫ СЧИСЛЕНИЯ. 10 3.2. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ. 14 В любой науке есть фундамент, без которого невозможно правильное понимание ее прикладных аспектов (пример: математика – теория чисел, теория множеств, мат. логика и др.). Так же и с информатикой – можно изучить насколько программ и даже научиться программировать на каком-то одном языке, но это не вся информатика, не самая главная и интересная ее часть. Теоретическая информатика складывается из ряда разделов математики: теории алгоритмов, теории автоматов, математической логики, теории формальных языков и грамматик, реляционной алгебры, теории информации и др. Теоретическая информатики старается методами точного анализа ответить на вопросы, возникающие при работе с информацией (пример: вопрос о количестве информации, наиболее рациональной организации для хранения и поиска нужной информации и др.). Изучение и понимание теоретических основ информатики является необходимым условием для того, чтобы стать специалистом в этой науке. Другое дело – с какой глубиной изучать. Многие разделы теоретической информатики достаточно сложны и требуют серьезной математической подготовке. Далее они будут рассмотрены скорее в ознакомительном порядке, с целью составить о них отчетливое представление.
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

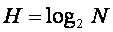 (1)
(1)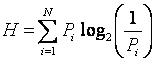 (2)
(2)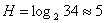 бит. Однако, в русских словах (и в словах других языков) различные буквы встречаются неодинаково часто. Если воспользоваться таблицей частотности букв русского языка и формулой (2), то получится несколько меньший результат: 4,72бит.
бит. Однако, в русских словах (и в словах других языков) различные буквы встречаются неодинаково часто. Если воспользоваться таблицей частотности букв русского языка и формулой (2), то получится несколько меньший результат: 4,72бит.