Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визуализация результатов тестовых измеренийСодержание книги
Поиск на нашем сайте
Стремление визуализировать формальные результаты тестовых измерений, получить определенную геометрическую интерпретацию результатов характерно для многих зарубежных исследователей. Наиболее удачной в данном отношении является работа [59]. В ней процесс визуализации разбивается на ряд этапов. На первом интерпретируется связь между наблюдаемыми результатами измерения и шкалой, ассоциируемой с осью. В рамках принятого ранее в тексте пособия соглашения о существовании сырых баллов — наблюдаемых результатов выполнения теста и производных показателей, принимаемых за истинные оценки учеников, — необходимо решить вопрос о характере величин, откладываемых на шкале. Если под шкалой понимается средство для отображения непрерывных свойств объекта, то речь, скорее всего, должна идти о производных показателях, вернее, о тех из них, которые в какой-то степени способны отражать идею непрерывности распределения. В целом вопрос выбора шкалы непосредственно связан с принятыми уровнем и методами измерения, поскольку различные шкалы предоставляют разные возможности для оперирования статистическими методами при переходе от наблюдаемых результатов выполнения теста к производным показателям. Подробно типы шкал и виды производных показателей будут рассматриваться в гл. 7. Что касается данного раздела, то здесь разумнее обратиться к обобщенному понятию переменной, конкретизация значений которой дает представление о результатах выполнения теста данной выборкой учеников. Идея взаимосвязи результатов измерения и положения испытуемого на оси переменной, ассоциируемой со шкалой в одномерном случае, когда по результатам выполнения теста выстраивается только одна шкала, представлена на рис. 2.5. Каждый результат измерения характеристики учащегося из тестируемой группы соответствует одной точке оси, а каждая точка определяет положение испытуемого или даже группы испытуемых с одинаковым тестовым баллом. На изображенной оси более высокие баллы располагаются правее, низкие — левее. Крайний слева результат обычно характерен для случая, когда испытуемый выполнил правильно лишь несколько заданий теста. Противоположный случай, когда ученик выполнил все или почти все, соответствует крайней правой точке на оси переменной измерения. Остальные точки занимают некоторое промежуточное положение между описанными выше экстремальными ситуациями
. Второй этап визуализации нацелен на интерпретацию связи между отдельными значениями переменной и совокупностью различных по трудности заданий теста. Общий подход к интерпретации основан на операционализа-ции понятия измерения. Результаты операционализации позволяют поставить в соответствие каждой точке оси переменной определенное число правильно выполненных заданий теста. Естественно предположить, что более трудные задания смещены вдоль оси вправо, так как их, скорее всего, будут выполнять правильно наиболее сильные испытуемые группы. Наоборот, более легкие задания будут смещены влево — они по силам ученикам с низким уровнем подготовки. Таким образом, при расположении заданий на оси переменной можно придерживаться следующего правила: чем выше уровень подготовки тестируемой группы учеников, тем правее расположены задания, поскольку сильным ученикам по плечу наиболее трудные задания теста. Если ранее на основании предварительного сбора статистических данных были получены устойчивые оценки параметра трудности заданий, то появляется возможность упорядочения заданий в рамках определенной стратегии предъявления их тестируемой группе учеников. Обычно в гомогенных педагогических тестах задания ранжируют по нарастанию трудности от начала к концу теста. Формально это утверждение можно представить в виде
где Пример расположения заданий возрастающей трудности показан на рис. 2.6. Из дидактических соображений рассматривается случай выполнения небольшого числа заданий, однако все положения, развиваемые на этом примере, применимы к любому числу заданий и к любому ученику тестируемой группы. Для иллюстрации идеи операционализации на рисунке указано положение истинного балла ученика на оси переменной для случая, когда правильно были выполнены три из ранжированных по нарастанию трудности четырех заданий теста.
Нетрудно понять, что локализация места расположения результата ученика на оси переменной зависит в основном от соотношения между величиной его истинного балла и трудностью заданий теста. Если балл ученика довольно высок, а задание достаточно легкое, то у ученика есть все основания для успешного выполнения этого задания теста. В противном случае, когда соотношение между упомянутыми выше величинами меняется на противоположное, у ученика есть веские основания для неуспеха. Конечно, наверняка предугадать ничего нельзя. Обычно говорят лишь о некоторой вероятности успеха или неуспеха.
ИСТОЧНИКИ ОШИБОК ИЗМЕРЕНИЯ Вероятностный характер наблюдаемых результатов выполнения теста обусловлен влиянием различных факторов, способствующих возникновению ошибок измерения. Среди этих факторов, действующих независимо друг от друга, выделяют случайные и неслучайные. К числу последних принадлежат те, которые появляются из-за просчетов разработчиков в процессе создания теста. К случайным факторам можно отнести настроение испытуемого, поведение экзаменатора, обстановку при тестировании в классе и многое другое — словом, все то, что учесть и предвидеть при тестировании попросту невозможно. Совсем иначе обстоит дело с неслучайными факторами, порождающими систематические ошибки в процессе измерения. Ошибки систематического характера возникают из-за неудачного выбора подхода к созданию теста либо вследствие применения малоэффективной технологии при его разработке. К ним могут привести нарушения требований методики сбора статистических данных, некачественная интерпретация результатов выполнения теста и ряд других факторов, действие которых разработчики тестов обычно стремятся свести к нулю или хотя бы значительно уменьшить, чтобы не выйти за пределы допустимой ошибки измерения.
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.185.202 (0.01 с.) |


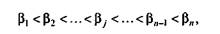
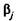 — уровень трудности j-го задания, j= 1, 2,..., п; п — число заданий в тесте.
— уровень трудности j-го задания, j= 1, 2,..., п; п — число заданий в тесте.