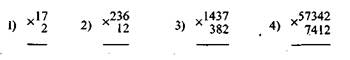Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визуализация истинных баллов тестируемыхСодержание книги
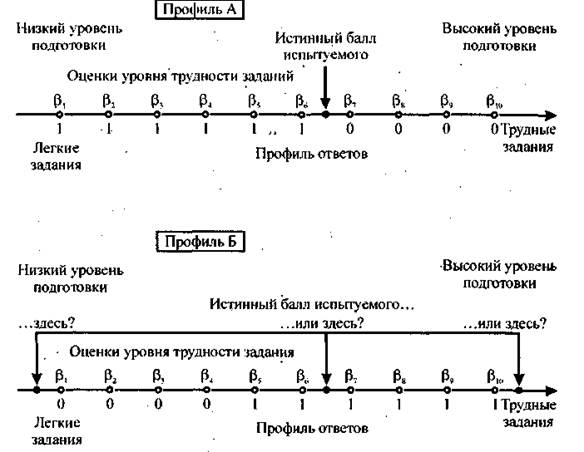
Поиск на нашем сайте Представляет интерес анализ обратной ситуации, когда после определенной работы в тесте остались только валидные задания и можно оценить состоятельность профилей ответов испытуемых, а не заданий теста. Ситуация с испытуемыми осложняется тем, что их нельзя просто и легко исключить из рассмотрения как несостоятельные задания. Ученики выполняли тест, и в любом случае они должны получить свои оценки, причем не любые, смещенные в сторону занижения или завышения, а те, которые отражают реальную картину подготовки тестируемой группы. Проблема получения истинных баллов выглядит достаточно тривиально для случая состоятельных профилей ответов на задания теста. Однако она значительно осложняется для тех испытуемых, ответы которых не вписываются в рассматриваемую схему. Ситуация с несостоятельными профилями ответов учеников довольно сложна и требует дополнительного обсуждения. На рис. 2.7 представлены профили ответов двух испытуемых на одни и те же 10 заданий теста, ранжированных по нарастанию трудности и расположенных вдоль оси переменной измерения. Уровень подготовки испытуемых оказался одинаковым, поскольку каждый из них выполнил по шесть заданий, однако не одних и тех же, а разных по трудности из представленных десяти заданий теста.
Рис. 2.7. Положение истинных баллов испытуемых для правильного (А) и инвертированного (Б) профилей ответов на оси переменной измерения Профиль А отличается явной состоятельностью. В нем приведены результаты испытуемого, который выполнил правильно подряд шесть наиболее легких заданий и не справился с четырьмя более трудными заданиями теста. Для педагога подобный профиль интересен тем, что в нем наглядно представлен так называемый кумулятивный эффект, когда правильный ответ на шестое задание обеспечивает воспроизводимость правильных ответов на более легкие предшествующие задания теста. Конечно, стойкий кумулятивный эффект наблюдается далеко не всегда, в основном для заданий, довольно тесно связанных по содержанию. В англоязычной методической литературе популярен пример заданий на умножение
который вполне ясно, хотя и довольно упрощенно, иллюстрирует идеи кумулятивное™ на практике. Действительно, если испытуемый умеет умножать на четырехзначное число, то он тем более справится с умножением на трех-, двух- и однозначные числа. Конечно, в процессе выполнения заданий нельзя исключать возможность случайных ошибок по невнимательности, простых описок, которые могут внести элементы инвертированности в правильные профили ответов. Однако в целом, если в тест отобраны состоятельные задания, содержание которых обеспечивает оценку значений планируемой переменной измерения, то есть надежда на стойкий кумулятивный эффект в профилях ответов учеников. В противном случае при возникновении инвертированных профилей у педагога появляются основания для вывода о низком качестве подготовки учеников и, соответственно, о низкой эффективности своей работы. Для подобных нежелательных выводов есть веские основания, поскольку в процессе обучения не была обеспечена реализация важнейшей цели, которую большинство педагогов трактует как формирование правильной структуры, а не объема знаний учеников. Возвращаясь к профилю А, необходимо решить вопрос с выбором точки на оси переменной измерения, соответствующей истинному баллу первого ученика. Естественно предположить, что эта точка расположена между шестым и седьмым заданиями теста. Положение точки левее седьмого задания выглядит вполне закономерным, так как испытуемый не выполнил правильно ни одного начиная с седьмого задания теста. Продвижение к искомой точке с другого конца теста дает столь же определенную картину: учащийся выполнил правильно шесть заданий и потому его истинный балл должен быть никак не меньше шести. У читателя может возникнуть вопрос обоснования возможного превышения наблюдаемого балла при оценке истинного уровня подготовки ученика, а именно: насколько правомерно считать, что истинный балл больше 6 либо почему при оценке истинного результата нельзя ограничиться наблюдаемым баллом 6? Ответ на вопрос будет выглядеть достаточно просто, если предположить, что между шестым и седьмым заданиями помещены еще несколько более трудных, чем шестое, но менее трудных, чем седьмое, заданий теста. Успех ученика при их выполнении будет выглядеть вполне закономерно, поскольку они все же легче, чем седьмое задание теста. Из этого рассуждения вытекает возможность смещения точки локализации истинного балла вправо от наблюдаемого балла вдоль оси переменной измерения. Есть и другой не менее веский аргумент в пользу выбора точки локализации истинного балла между шестым и седьмым заданиями теста — идея смещения хорошо увязывается с обшей концепцией истинной оценки как величины, не зависящей от подбора заданий теста. В отличие от предыдущего случая выбор предположительного места локализации истинного балла второго ученика с профилем ответов Б — задача довольно непростая. К. тому же сам по себе профиль Б трудно объясним в силу своей явной несостоятельности: ученик не справился с четырьмя наиболее легкими заданиями и вместе с тем выполнил верно шесть более трудных заданий теста. Сложность выбора места локализации истинного балла для профиля Б становится вполне явной, если рассмотреть гипотетические экстремальные ситуации. Предположим, что точка, соответствующая истинному баллу второго ученика, находится на оси правее самого трудного десятого задания, что в какой-то мере вполне оправданно, так как ученик выполнил верно десятое задание теста. Однако тогда не ясно, как увязать принятое предположение с фактом неправильного выполнения первых четырех более легких заданий теста. Столь же непонятным остается общее решение задачи локализации, если пойти по другому пути и поставить в центр внимания неправильно выполненные учеником задания теста. В этом случае точку локализации истинного балла ученика необходимо выбрать левее самого легкого задания с оценкой трудности £,, что представляется довольно неразумным и плохо согласуется с естественной логикой, так как шесть наиболее трудных заданий были выполнены учеником верно. К сожалению, для профиля Б трудно, а скорее просто невозможно найти разумное решение, поскольку в равной степени алогичным кажется любое другое расположение истинного балла ученика между точками, локализующими положение заданий на оси переменной измерения. Таким образом, стремление педагога оценить всех учеников, выполнявших тест, нельзя признать рациональным, так как задача становится неразрешимой для случая инвертированных профилей ответов учеников. Здесь выявляется определенная закономерность: чем выше мера инвертированности профиля ответа ученика, тем меньше оснований для реализации основной цели измерения — определения истинного балла каждого ученика тестируемой группы. Конечно, причины несостоятельности профилей ответов учеников могут быть самыми разными. Далеко не все инверсии в профилях указывают на некачественную структуру знаний испытуемого. Например, возможна ситуация, когда ученик нарушил предлагаемый порядок расположения заданий в тесте при их выполнении и сосредоточил все усилия на самых трудных заданиях из конца теста, а к легким не успел приступить. Быть может, имели место ошибки разработчика при оценке значений параметра трудности заданий либо при ранжировании заданий по нарастанию трудности в тесте. Возможно, в процессе создания теста отсутствовал этап отбора заданий с несостоятельными профилями либо представленные в тесте задания не обладают четко выраженным кумулятивным эффектом из-за особенностей содержания теста. Окончательный вывод должен принадлежать педагогу-разработчику, поскольку именно он знаком со всеми обстоятельствами, сопутствовавшими процессам создания и применения теста. Для уточнения вывода представляет интерес сравнительный анализ результатов выполнения теста, который помогает сузить круг возможных причин инверсий в профилях ответов учеников. Сформулированное утверждение удачно иллюстрируется данными примера на рис. 2.7. Не обладая дополнительными сведениями, легко предположить, что причиной инвертированности профиля Б является несостоятельность отдельных заданий теста. О том, что предположение неверно и здесь имеет место несостоятельность второго испытуемого, а не заданий, свидетельствуют результаты первого ученика, у которого в профиле А все распределяется закономерно. Естественно, что для планирования процесса обучения наибольший интерес представляет профиль Б, причины несостоятельности которого педагогу предстоит выяснить в процессе непосредственного общения с учеником по результатам выполнения теста.
|
||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |