
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Моделирование случайных событий и случайных величинСтр 1 из 4Следующая ⇒
Тема: Моделирование случайных событий и случайных величин План лекции: 1. Моделирование независимых случайных событий. 2. Моделирование группы несовместных событий. 3. Моделирование условного события. 4. Моделирование дискретной случайной величины. 5. Моделирование дискретной случайной величины с геометрическим распределением. 6. Моделирование дискретной случайной величины с биномиальным распределением. 7. Моделирование дискретной случайной величины с распределением Пуассона. 8. Метод обратной функции. 9. Моделирование непрерывной случайной величины с равномерным распределением. 10. Моделирование непрерывной случайной величины с экспоненциальным законом распределения. 11. Моделирование пуассоновского потока. 12. Моделирование непрерывной случайной величины с нормальным законом распределения. 13. Моделирование непрерывной случайной величины с логарифмически-нормальным законом распределения. 14. Моделирование распределения и потоков Эрланга. 15. Моделирование непрерывной случайной величины с гамма - распределением. 16. Моделирование непрерывной случайной величины с бета - распределением. 17. Моделирование непрерывной случайной величины с распределением Вейбулла. 18. Моделирование непрерывной случайной величины с гипер - и гипоэкспоненциальным распределением. 19. Моделирование случайных процессов. 20. Моделирование случайных векторов. Моделирование независимых случайных событий Допустим, что вероятность наступления некоторого элементарного случайного события
Рис.1. Моделирование наступления случайных событий Действительно, если Эта модель хорошо описывает такие события, как обслуживание требования в устройстве СМО, которое может быть свободным или занятым, успешную или нет попытку выполнения некоторого задания, попадание или нет в цель, разветвление потоков информации в двух и более направлениях. В некоторых языках для моделирования случайного события используется специальный блок (например, в языке
Моделирование дискретной случайной величины С распределением Пуассона Случайную величину с распределением Пуассона можно получить, если допустить, что число независимых испытаний
Распределение Пуассона является граничным случаем биномиального распределения и описывает случайные события, которые имеют место очень редко. На практике по биномиальному закону распределяются: количество дефектов в готовом изделии, количество аварий на транспорте за некоторый продолжительный промежуток времени, количество звонков в телефонной сети в единицу времени и др. Чтобы получить случайную величину
В случае выполнения условия (2) число Метод обратной функции Рассмотрис метод моделирования случайной величины, которая имеет функцию плотности распределения Действительно, если на оси ординат отметить значение
Рис. 1. Применение метода обратной функции для генерирования непрерывной случайной величины Таким образом, последовательность случайных чисел - генерируются случайные числа - вычисляется случайное число
С гамма - распределением Случайная величина
Математическое ожидание и дисперсия случайной величины X с гамма - распределением определяются по формулам: Свойство гамма -распределения: Сумма любого количества независимых гамма-распределенных случайных величин m с одинаковым значением параметра β также подчиняется гамма-распределению, но с параметрами (α1 + а2 +... + ат) и β. Методы моделирования случайной величины с гамма - распределением
От случайной величины
Основная проблема, которая возникает при моделировании гамма - распределения, - это вычисление гамма - функции. Чтобы получить значения гамма - функции можно воспользоваться следующей формулой:
Вычисление гамма - функции для разных значений ещё усложняется тем, что она зависит от трёх аргументов (x,α,β). Поэтому при моделировании на практике в формуле функции плотности используется неполная гамма-функция
для вычисления которой при условии, что α < 1 можно воспользоваться таким выражением:
Для α > 1 интеграл можно легко вычислить с помощью любых формул численного интегрирования. Полученная функция плотности гамма - распределения используется для преобразования случайных независимых равномерно распределенных величин. Для этого область возможных значений случайной величины X разбивается на n одинаковых интервалов, количество которых зависит от заданной точности аппроксимации функции f(х). Потом с помощью значения Для оценивания близкости функции плотности распределения вероятностей полученных значений случайной величины к функции плотности распределения используют метод наименьших квадратов. С распределением Вейбулла
Случайная величина X имеет нормальное распределение Вейбулла, если его плотность и функция распределения вероятностей описываются выражениями:
Математическое ожидание и дисперсия случайной величины X определяются по формулам:
Распределению Вейбула подчиняются значения случайной величины, которые определяют протяженность безотказной работы сложной системы из нескольких объектов, при условии, что из строя могут выходить отдельные объекты. Для моделирования случайных величин wi, распределенных по закону Вейбулла, используются независимые равномерно распределенные на промежутке [0,1] случайные величины, которые преобразуются методом обратной функции:
где 1/λ0 — параметр масштаба; α – параметр крутизны. Тема: Моделирование случайных событий и случайных величин План лекции: 1. Моделирование независимых случайных событий. 2. Моделирование группы несовместных событий. 3. Моделирование условного события. 4. Моделирование дискретной случайной величины. 5. Моделирование дискретной случайной величины с геометрическим распределением. 6. Моделирование дискретной случайной величины с биномиальным распределением. 7. Моделирование дискретной случайной величины с распределением Пуассона. 8. Метод обратной функции. 9. Моделирование непрерывной случайной величины с равномерным распределением. 10. Моделирование непрерывной случайной величины с экспоненциальным законом распределения. 11. Моделирование пуассоновского потока. 12. Моделирование непрерывной случайной величины с нормальным законом распределения. 13. Моделирование непрерывной случайной величины с логарифмически-нормальным законом распределения. 14. Моделирование распределения и потоков Эрланга. 15. Моделирование непрерывной случайной величины с гамма - распределением. 16. Моделирование непрерывной случайной величины с бета - распределением. 17. Моделирование непрерывной случайной величины с распределением Вейбулла. 18. Моделирование непрерывной случайной величины с гипер - и гипоэкспоненциальным распределением. 19. Моделирование случайных процессов. 20. Моделирование случайных векторов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.154.151 (0.029 с.) |
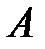 в одном испытании равна
в одном испытании равна 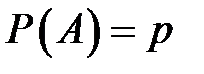 . Считается, что условия проведения каждого испытания одинаковые и его можно повторить бесконечное количество раз. Если
. Считается, что условия проведения каждого испытания одинаковые и его можно повторить бесконечное количество раз. Если 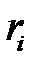 – это значения равномерно распределенной величины на
– это значения равномерно распределенной величины на 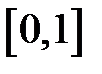 , то можно утверждать, что при условии
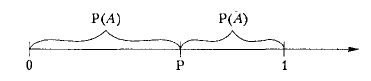
, то можно утверждать, что при условии 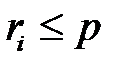 (рис.1) наступит событие
(рис.1) наступит событие 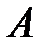 , а если
, а если 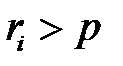 , то произойдет событие
, то произойдет событие 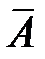 .
.
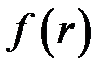 – функция плотности равномерно распределенной непрерывной случайной величины
– функция плотности равномерно распределенной непрерывной случайной величины 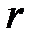 , то
, то 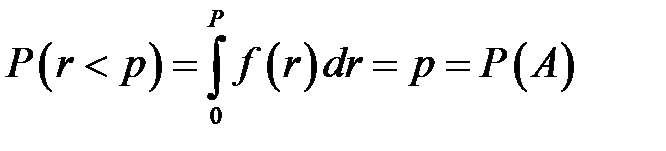 .
.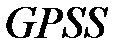 – блок
– блок 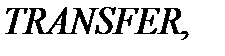 который работает в статистическом режиме).
который работает в статистическом режиме).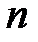 в биномиальном распределении стремится к бесконечности, а вероятность успешного испытания
в биномиальном распределении стремится к бесконечности, а вероятность успешного испытания 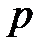 — к нулю, причем произведение
— к нулю, причем произведение 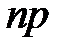 остается неизменным и равным
остается неизменным и равным 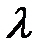 :
: 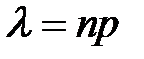 Функция плотности распределения Пуассона задаётся выражением
Функция плотности распределения Пуассона задаётся выражением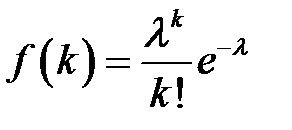 .
.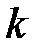 с распределением Пуассона, генерируем последовательность равномерно распределенных случайнных чисел
с распределением Пуассона, генерируем последовательность равномерно распределенных случайнных чисел 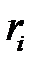 и находим их произведение, проверяя неравенство
и находим их произведение, проверяя неравенство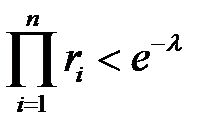 (2)
(2)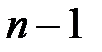 является случайной величиной, которая принадлежит совокупности, распределенной по закону Пуассона с математическим ожиданием
является случайной величиной, которая принадлежит совокупности, распределенной по закону Пуассона с математическим ожиданием 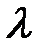 . Если условию (2) соответствует первое из чисел
. Если условию (2) соответствует первое из чисел 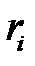 , то значение случайной величины
, то значение случайной величины 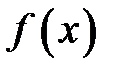 и монотонно возрастающую функцию распределения
и монотонно возрастающую функцию распределения 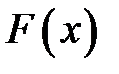 . Суть метода заключается в следующем. С помощью генератора случайных чисел генерируем значение случайной величины
. Суть метода заключается в следующем. С помощью генератора случайных чисел генерируем значение случайной величины 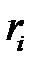 , которому соответствует точка на оси ординат. Значение случайной величины
, которому соответствует точка на оси ординат. Значение случайной величины 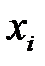 с функцией распределения
с функцией распределения 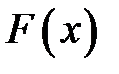 можем получить из уравнения
можем получить из уравнения 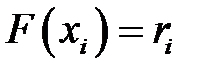 .
.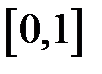 , и на оси абсцисс найти значение
, и на оси абсцисс найти значение 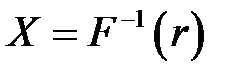 будет иметь функцию распределения
будет иметь функцию распределения 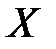 равна вероятности
равна вероятности 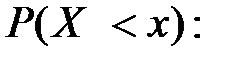
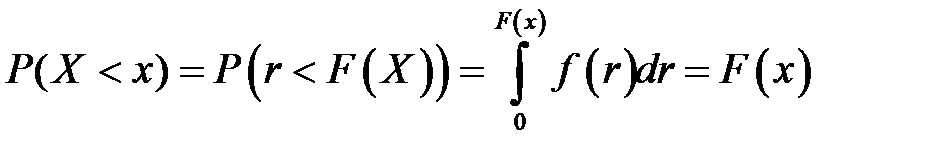
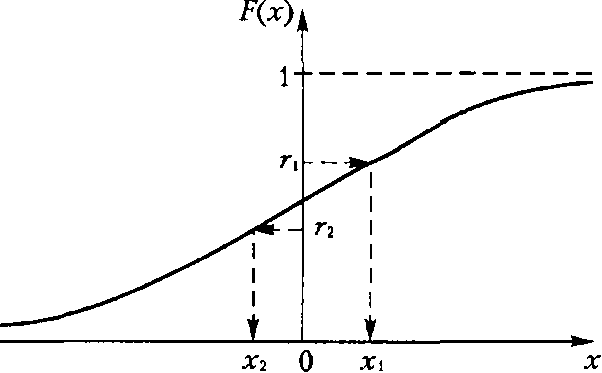
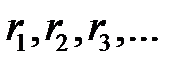 превращается в последовательность
превращается в последовательность 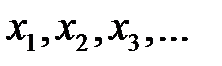 , которая имеет заданную функцию плотности распределения
, которая имеет заданную функцию плотности распределения 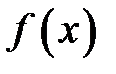 . Откуда следует общий алгоритм моделирования непрерывных случайных величин, имеющих заданную функцию распределения вероятностей:
. Откуда следует общий алгоритм моделирования непрерывных случайных величин, имеющих заданную функцию распределения вероятностей: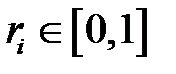 ;
;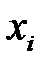 , которое является решением уравнения:
, которое является решением уравнения: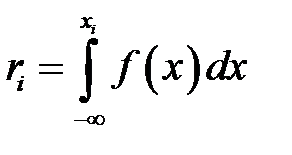
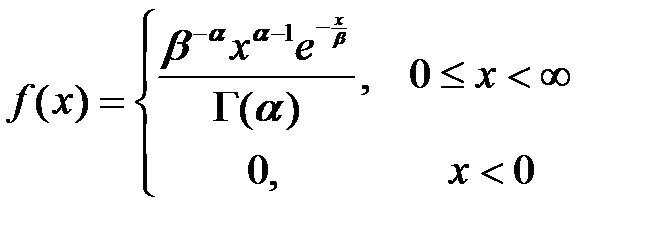 ,
, 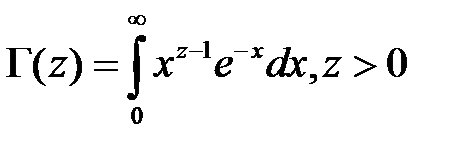 .
.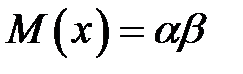 ;
; 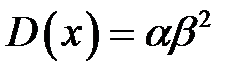
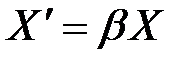 .
.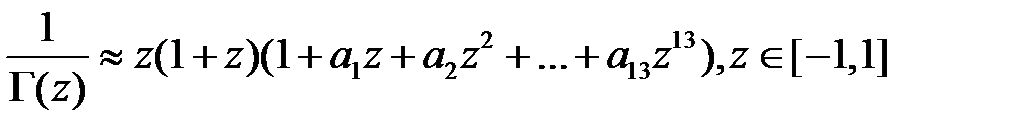
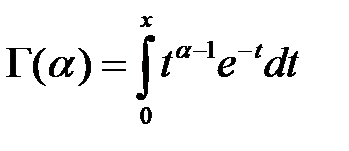 .,
.,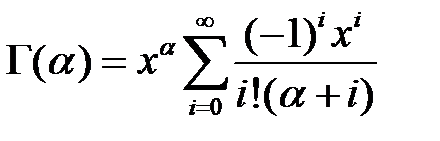 .
.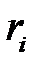 , (методом розыгрыша по жребию) выбирается один из n интервалов, в котором получают случайные числа с функцией плотности распределения f(х).
, (методом розыгрыша по жребию) выбирается один из n интервалов, в котором получают случайные числа с функцией плотности распределения f(х).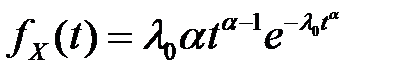 ,
, 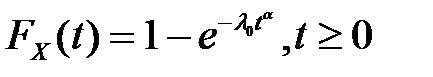 .
.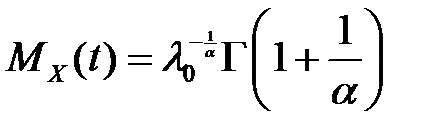 ;
; 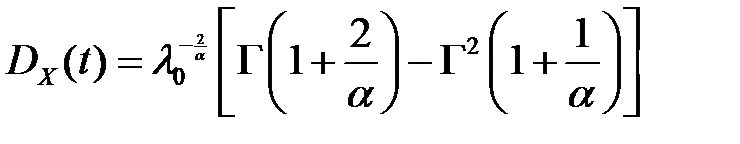 .
.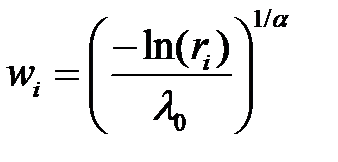 .
.


