
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С логарифмически-нормальным законом распределенияСодержание книги
Поиск на нашем сайте
Логарифмически-нормальное распределение – это такое распределение случайной величины, в которой нормальное распределение имеет натуральный логарифм её значений. Это распределение применимо для моделирования мультипликативных процессов так же, как и нормальное распределение – для аддитивных процессов. Можно показать, что произведение независимых положительных случайных величин стремится к логарифмически-нормальному распределению. Случайная величина
где Значения случайной величины х с логарифмически-нормальным распределением всегда положительные и используются при моделировании экономических, физических, биологических систем многих типов. Случайными величинами с этим распределением являются, в частности, размер банковского вклада, длина слов определенного языка и переданных сообщений в сети, размеры файлов, которые хранятся в компьютере. Метод моделирования логарифмически-нормального распределения предусматривает подстановку в уравнение
Моделирование распределения и потоков Эрланга Случайные величины с экспоненциальным распределением не всегда адекватно описывают некоторые реальные процессы и события, например, время обслуживания и моменты поступления требований в СМО. Для более точного моделирования таких процессов и событий целесообразно использовать случайные величины, которые имеют распределение Эрланга. Функция плотности распределения Эрланга
Математическое ожидание и дисперсия распределения Эрланга определяются по формулам:
Для моделирования распределения Эрланга используют метод свёрток случайных величин с экспоненциальными функциями распределения. Для этого нужно лишь вычислить сумму
Моделирование непрерывной случайной величины С гамма - распределением Случайная величина
Математическое ожидание и дисперсия случайной величины X с гамма - распределением определяются по формулам: Свойство гамма -распределения: Сумма любого количества независимых гамма-распределенных случайных величин m с одинаковым значением параметра β также подчиняется гамма-распределению, но с параметрами (α1 + а2 +... + ат) и β. Методы моделирования случайной величины с гамма - распределением
От случайной величины
Основная проблема, которая возникает при моделировании гамма - распределения, - это вычисление гамма - функции. Чтобы получить значения гамма - функции можно воспользоваться следующей формулой:
Вычисление гамма - функции для разных значений ещё усложняется тем, что она зависит от трёх аргументов (x,α,β). Поэтому при моделировании на практике в формуле функции плотности используется неполная гамма-функция
для вычисления которой при условии, что α < 1 можно воспользоваться таким выражением:
Для α > 1 интеграл можно легко вычислить с помощью любых формул численного интегрирования. Полученная функция плотности гамма - распределения используется для преобразования случайных независимых равномерно распределенных величин. Для этого область возможных значений случайной величины X разбивается на n одинаковых интервалов, количество которых зависит от заданной точности аппроксимации функции f(х). Потом с помощью значения
Для оценивания близкости функции плотности распределения вероятностей полученных значений случайной величины к функции плотности распределения используют метод наименьших квадратов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.006 с.) |

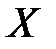 имеет логарифмически-нормальный закон распределения вероятностей, если
имеет логарифмически-нормальный закон распределения вероятностей, если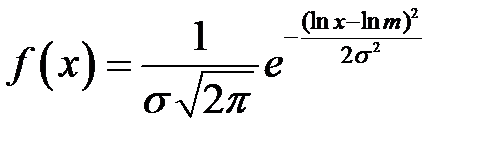 ,
, 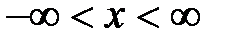
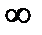 ,
,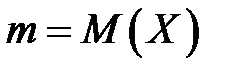 ,
, 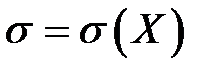 .
.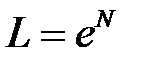 значений из выборки
значений из выборки 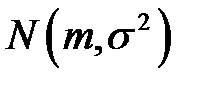 , которые имеют нормальное распределение с математическим ожиданием m и дисперсией σ 2, где L — логарифмически-нормальное распределение. Характеристики этого распределения:
, которые имеют нормальное распределение с математическим ожиданием m и дисперсией σ 2, где L — логарифмически-нормальное распределение. Характеристики этого распределения: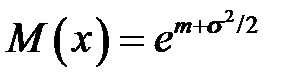 ,
, 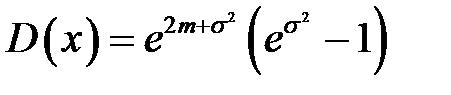 .
.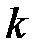 -го порядка с интенсивностью
-го порядка с интенсивностью 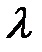 имеет вид:
имеет вид: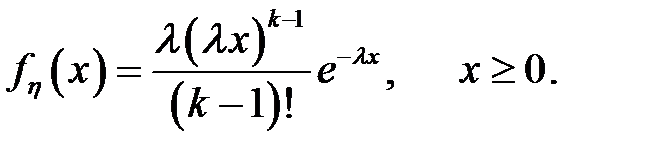
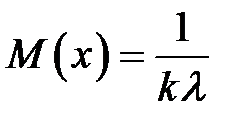 ;
; 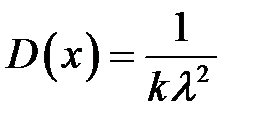
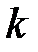 экспоненциально распределенных случайных величин. С увеличением
экспоненциально распределенных случайных величин. С увеличением 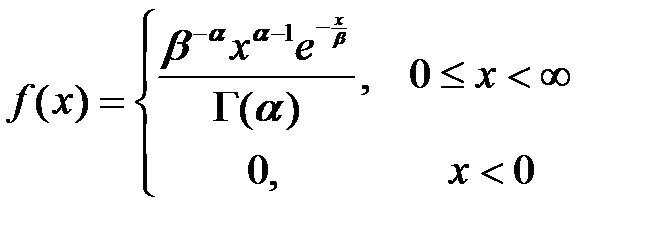 ,
, 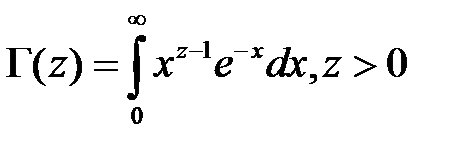 .
.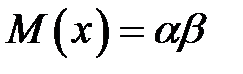 ;
; 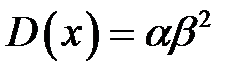
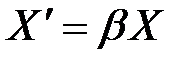 .
.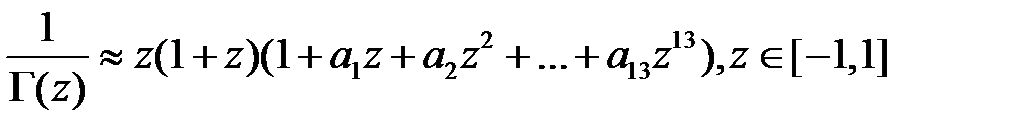
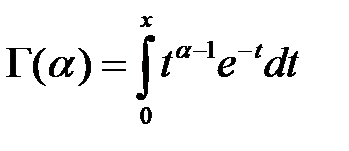 .,
.,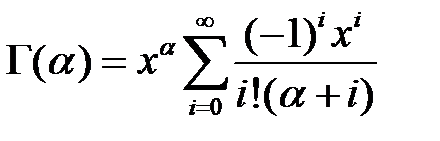 .
.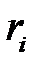 , (методом розыгрыша по жребию) выбирается один из n интервалов, в котором получают случайные числа с функцией плотности распределения f(х).
, (методом розыгрыша по жребию) выбирается один из n интервалов, в котором получают случайные числа с функцией плотности распределения f(х).


