Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С геометрическим распределением
Для моделирования случайной величины
Примером случайной величины с таким распределением может быть общее количество испытаний, которые нужно провести до первого успешного испытания. Вероятность того, что случайная величина принимает значение
Для моделирования случайной величины с геометрическим распределениемможно использовать таблицю закона распределения или метод обратной функции. Поскольку при больших
Моделирование дискретной случайной величины С биномиальным распределением Биномиальное распределение, или распределение Бернулли, – это распределение дискретной случайной величины, которая принимает два и только два значения: 1 – «true», или «истина», и 0 — «false», или «ложь». Это распределение показывает вероятность появления некоторого события при выполнении
Функция распределения вероятностей имеет вид:
В зависимости от значения 1) При небольших 2) При больших значениях
где
Значение случайной величины с биномиальным распределением равно количеству испытаний Моделирование дискретной случайной величины С распределением Пуассона Случайную величину с распределением Пуассона можно получить, если допустить, что число независимых испытаний
Распределение Пуассона является граничным случаем биномиального распределения и описывает случайные события, которые имеют место очень редко. На практике по биномиальному закону распределяются: количество дефектов в готовом изделии, количество аварий на транспорте за некоторый продолжительный промежуток времени, количество звонков в телефонной сети в единицу времени и др. Чтобы получить случайную величину
В случае выполнения условия (2) число Метод обратной функции Рассмотрис метод моделирования случайной величины, которая имеет функцию плотности распределения Действительно, если на оси ординат отметить значение
Рис. 1. Применение метода обратной функции для генерирования непрерывной случайной величины Таким образом, последовательность случайных чисел
- генерируются случайные числа - вычисляется случайное число
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.35.77 (0.007 с.) |
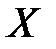 с геометрическим распределениемнеобходимо задать таблицу её значений и их вероятностей
с геометрическим распределениемнеобходимо задать таблицу её значений и их вероятностей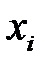
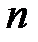
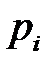
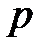
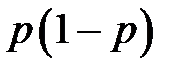
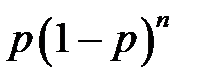
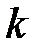 , определяется по формуле:
, определяется по формуле: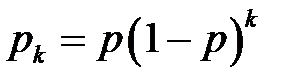 ,
, 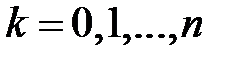
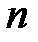 эти методы требуют много компьютерного времени, то для нахождения значений случайной величины с геометрическим распределениемиспользуют формулу:
эти методы требуют много компьютерного времени, то для нахождения значений случайной величины с геометрическим распределениемиспользуют формулу: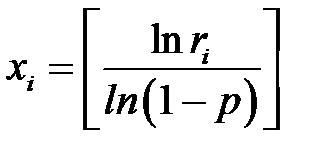 ,
, 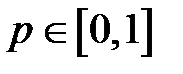 (где
(где 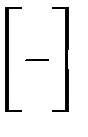 – обозначение целой части числа).
– обозначение целой части числа).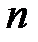 независимых повторных испытаний, в каждом из которых событие наступает с вероятностью
независимых повторных испытаний, в каждом из которых событие наступает с вероятностью 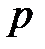 , т.е. вероятность
, т.е. вероятность 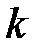 успешных следствий в
успешных следствий в 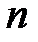 испытаниях
испытаниях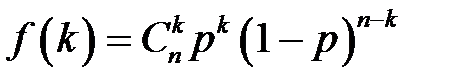
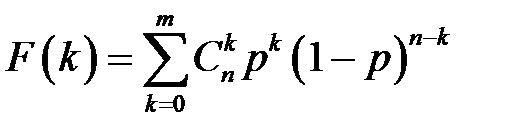 ,
, 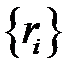 из
из 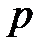 .
.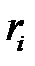 до тех пор, пока не выполняется условие
до тех пор, пока не выполняется условие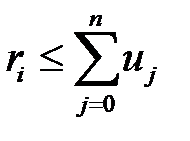 , (1)
, (1)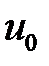 и
и 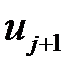 задаются выражениями
задаются выражениями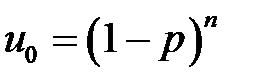 и
и 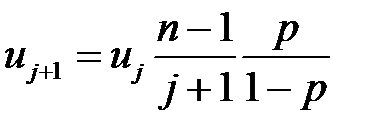
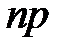 остается неизменным и равным
остается неизменным и равным 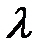 :
: 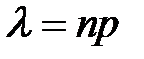 Функция плотности распределения Пуассона задаётся выражением
Функция плотности распределения Пуассона задаётся выражением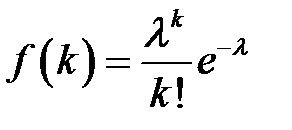 .
.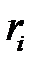 и находим их произведение, проверяя неравенство
и находим их произведение, проверяя неравенство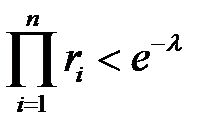 (2)
(2)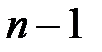 является случайной величиной, которая принадлежит совокупности, распределенной по закону Пуассона с математическим ожиданием
является случайной величиной, которая принадлежит совокупности, распределенной по закону Пуассона с математическим ожиданием 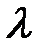 . Если условию (2) соответствует первое из чисел
. Если условию (2) соответствует первое из чисел 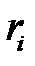 , то значение случайной величины
, то значение случайной величины 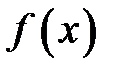 и монотонно возрастающую функцию распределения
и монотонно возрастающую функцию распределения 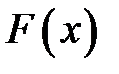 . Суть метода заключается в следующем. С помощью генератора случайных чисел генерируем значение случайной величины
. Суть метода заключается в следующем. С помощью генератора случайных чисел генерируем значение случайной величины 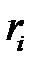 , которому соответствует точка на оси ординат. Значение случайной величины
, которому соответствует точка на оси ординат. Значение случайной величины 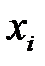 с функцией распределения
с функцией распределения 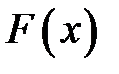 можем получить из уравнения
можем получить из уравнения 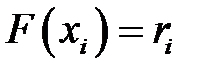 .
.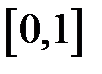 , и на оси абсцисс найти значение
, и на оси абсцисс найти значение 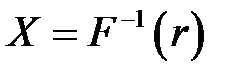 будет иметь функцию распределения
будет иметь функцию распределения 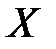 равна вероятности
равна вероятности 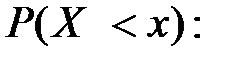
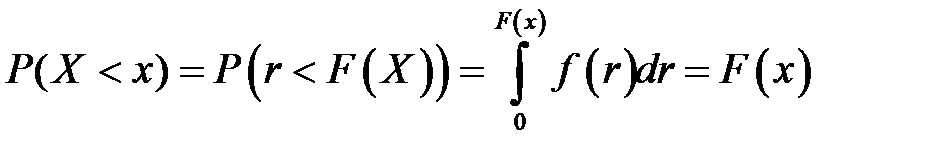
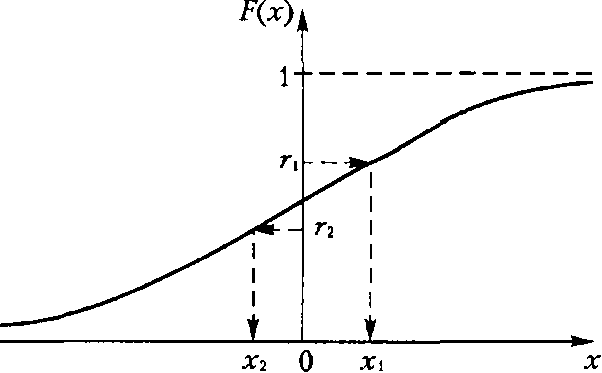
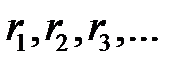 превращается в последовательность
превращается в последовательность 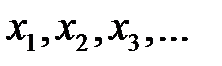 , которая имеет заданную функцию плотности распределения
, которая имеет заданную функцию плотности распределения 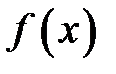 . Откуда следует общий алгоритм моделирования непрерывных случайных величин, имеющих заданную функцию распределения вероятностей:
. Откуда следует общий алгоритм моделирования непрерывных случайных величин, имеющих заданную функцию распределения вероятностей: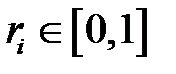 ;
;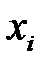 , которое является решением уравнения:
, которое является решением уравнения: