Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые звенья систем автоматического регулирования
Любая система автоматического регулирования состоит из ряда звеньев, каждое из которых обладает определенными динамическими свойствами. В зависимости от характера протекания переходного процесса различают следующие типовые звенья систем автоматического регулирования: - дифференцирующее; - усилительное; - интегрирующее; - апериодическое; - колебательное; - звено чистого запаздывания. Дифференцирующим звеном называют элемент, у которого скорость изменения выходного сигнала пропорциональна скорости изменения входного сигнала, т. е. пропорциональна первой производной от скорости изменения входного сигнала по времени. В соответствии с этим его дифференциальное уравнение имеет вид Y (t) = Kdx (t)/ dt, где К — коэффициент передачи звена. Переходная функция звена на единичное входное воздействие показана в соответствии с рисунком 12. Дифференцирующее звено может быть звеном первого и второго порядка.
Рисунок 12 Усилительным звеном является звено, позволяющее пропорционально изменять заданную величину в какое-то число раз. Переходная функция показана в соответствии с рисунком 13.
Рисунок 13 При этом выходной сигнал без запаздывания повторяет входной сигнал. Переходная характеристика звена в динамическом режиме описывается уравнением Y (t) = Kx (t), где К — коэффициент передачи звена. Интегрирующим звеном считают такое звено, выходная величина которого пропорциональна интегралу по времени от входной, т. е. Y (t) = K где К — коэффициент передачи звена. Переходная функция показана в соответствии с рисунком 14.
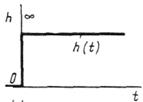
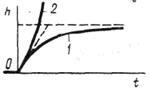
Рисунок 14 В апериодическом звене выходная величина при входном единичном скачкообразном воздействии изменяется по экспоненциальному закону, стремясь к определенному предельному значению в соответствии с рисунком 15. Выходной сигнал звена запаздывает по отношению к входному сигналу.
Рисунок 15 Переходная характеристика звена описывается дифференциальным уравнением
где В колебательном звене переходная функция при скачкообразном входном сигнале имеет форму колебаний, расходящихся (кривая 2 в соответствии с рисунком 16) для неустойчивого и затухающих (кривая 1 в соответствии с рисунком 16 ) для устойчивого звена.
Рисунок 16 Колебательное звено, так же как и апериодическое, содержит элементы, накапливающие энергию, и элементы, рассеивающие ее. Колебательную переходную характеристику имеют звенья, у которых дифференциальные уравнения имеют вид
при условии что Звено с чистым запаздыванием — это звено, в котором выходная величина идеально повторяет входную, но с отставанием на постоянный отрезок времени
Рисунок 17
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 99; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.248.24 (0.007 с.) |

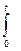 x (t) dt,
x (t) dt,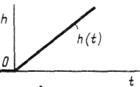

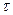 dy{t)/dt + Y(t) = Kx(t),
dy{t)/dt + Y(t) = Kx(t),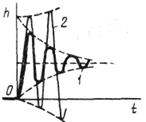
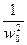
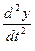 +
+ 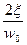
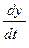 + Y = Kx
+ Y = Kx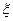 < l, где w 0 — резонансная угловая частота звена;
< l, где w 0 — резонансная угловая частота звена;