
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории автоматического регулирования
Теория автоматического регулирования — специальная наука, изучающая общие для всех замкнутых автоматических систем (вне зависимости от их физической сущности) принципы построения и методы исследования их статических и динамических свойств. Основными проблемами теории автоматического регулирования являются: - точность работы; - устойчивость; - качество переходных процессов системы автоматического регулирования. Однако в теории автоматического регулирования применяется весьма сложный математический аппарат, не рассматриваемый в программе учебного процесса, и поэтому в данном учебнике будут даны лишь элементы теории автоматического регулирования. Разработанная система должна удовлетворять определенным технологическим и энергетическим требованиям (максимальная и минимальная скорости процесса, диапазон регулирования, мощность, коэффициент усиления, от которого зависит статическая точность), требованиям надежности и т. д. На этапе исследования установившегося режима не всегда удается учесть внутренние ограничения, заложенные в систему и связанные с замыканием системы обратной связью. Эти ограничения можно учесть лишь при анализе работы системы в динамическом режиме. Анализ динамического режима позволяет получить данные об устойчивости замкнутой системы и об ее быстродействии, так как устойчивость определяет ее работоспособность, а быстродействие влияет на динамическую точность и производительность технологического оборудования. Динамический режим становится определяющим для систем, управляющих машинами, в которых необходимо получить высокую производительность. Система, устойчивая в установившемся режиме, часто оказывается неустойчивой в динамическом режиме. Неустойчивой считается система, если при снятии входного управляющего сигнала на выходе ее имеют место незатухающие колебания. Такая система непригодна к работе, так как возникающие в ней внутренние напряжения приводят к нарушению кинематических связей. Таким образом, одним из центральных вопросов, которые приходится решать при создании систем автоматического регулирования, работающих с обратной связью, является обеспечение их устойчивости. Устойчивость, быстродействие и коэффициент усиления, являясь основными критериями оценки качества работы системы, находятся между собой в противоречии, что вызывает необходимость поиска компромиссного решения.
Следует заметить, что дифференциальные уравнения, описывающие систему автоматического регулирования, являются, по сути дела, ее математической моделью, исследование которой позволяет получить значения критериев оценки с учетом заданной точности и производительности, а также влияния внешних воздействий. Система автоматического регулирования, как уже отмечалось, состоит из ряда элементов, каждый из которых выполняет определенные функции. Эти элементы при разработке математической модели заменяют простейшими типовыми элементами, которые называют звенья и для которых известны дифференциальные уравнения и необходимые характеристики. Представление системы в виде динамических звеньев, соединенных между собой соответствующим образом, позволяет значительно сократить время на построение математической модели. Однако наиболее развитые системы имеют математическую модель в виде сложных дифференциальных уравнений высокого порядка, решение которых в большинстве случаев невозможно. С целью упрощения исследования математической модели пользуются некоторыми методами, позволяющими преобразовать искомые выражения в их изображение. Таков, например, метод Лапласа — Карсона. Пользуясь этим методом, можно заменить функции времени U (t) в ее изображении
где Используя преобразования можно получить передаточную функцию рассматриваемой системы:
Из формулы передаточной функции получают изображения выходной величины: Y (p) = X (p) w (p). Пользуясь этим методом преобразования, можно описывать достаточно сложные системы автоматического регулирования. Однако этот метод дает достаточно хорошие результаты для линейных систем. Для нелинейных систем разработаны нелинейные методы. Применение нелинейных методов сопряжено с трудностями описания нелинейных элементов, и они используются для решения частных задач.
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 85; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.141.202 (0.005 с.) |
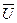 :
: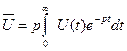
 ,
,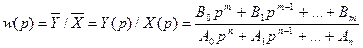 .
.


