Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силовой расчет структурной группы II класса 2-го порядка третьего видаСодержание книги
Поиск на нашем сайте
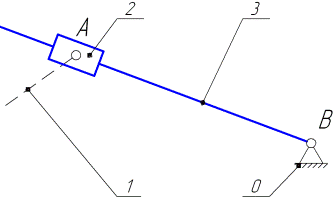
Рассмотрим особенности расчета промежуточной группы Ассура, у которой центральной кинематической парой является поступательная пара V класса (рис. 4.12).
Рис. 4.12
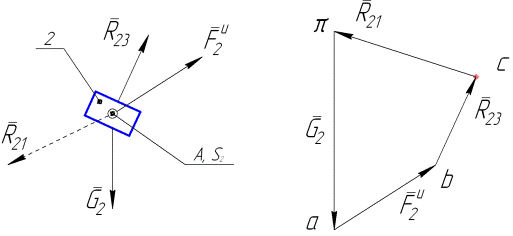
Сначала проанализируем возможность рассмотрения равновесия звеньев по отдельности.Выделяем, например, ползун 2, прикладываем к нему активные силы и силы реакции (рис. 4.13, а) и обнаруживаем, что ползун находится под действием системы сходящихся сил и векторное уравнение равновесия этой системы содержит три неизвестные: модуль реакции
а) б)
Рис. 4.13
Выделяем далее кулису 3 (рис. 4.13, б) и получаем расчетную схему тоже с тремя неизвестными (модуль реакции
Рис. 4.14
Записываем уравнение равновесия системы сил на рисунке 4.14 в векторной форме: В этом уравнении одна «лишняя» неизвестная, для отыскания которой имеет смысл обратиться к другому уравнению равновесия в форме суммы моментов сил относительно какого-либо центра. Этим центром может быть выбрана, например, точка А, и тогда уравнение равновесия «в моментах» запишется так:
Решаем это уравнение относительно
а) Рис. 4.15 б) Более рационально, однако, при составлении уравнения равновесия «в моментах» в качестве центра выбрать точку В. Тогда решением этого уравнения будет модуль реакции
В плане сил, построенном по этому уравнению, замыкающим вектором будет искомая реакция
Рис.4.16
Завершающей операцией в данном анализе является отыскание реакции Ползун находится под действием плоской системы сходящихся сил, соответственно условие его равновесия исчерпывается одним уравнением в векторной форме, или двумя алгебраическими уравнениями в координатной форме. Как и ранее, обращаемся к векторному уравнению
а) б)
Рис. 4.17
|
||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.92 (0.007 с.) |

 ,а также модуль и направление реакции
,а также модуль и направление реакции  . Из курса ТМ известно, что условие равновесия плоской системы сходящихся сил включает только два уравнения (в проекциях наосях координат), следовательно, в данном случае имеем статически неопределимую расчетную схему.
. Из курса ТМ известно, что условие равновесия плоской системы сходящихся сил включает только два уравнения (в проекциях наосях координат), следовательно, в данном случае имеем статически неопределимую расчетную схему.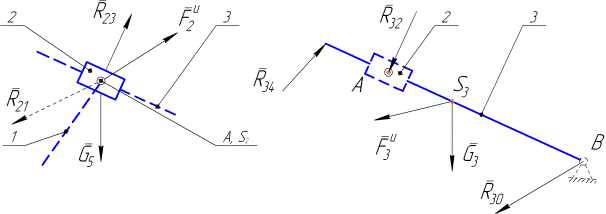
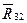 , модуль и направление реакции
, модуль и направление реакции 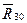 ). В данном случае тело (кулиса) находится под действием плоской системы сил, для исследования равновесия которой в курсе ТМ выведены три формы условия равновесия, каждая из которых включает три уравнения. Т.е. имеем статически определимую расчетную схему. Как и выше, выполним разложение реакции
). В данном случае тело (кулиса) находится под действием плоской системы сил, для исследования равновесия которой в курсе ТМ выведены три формы условия равновесия, каждая из которых включает три уравнения. Т.е. имеем статически определимую расчетную схему. Как и выше, выполним разложение реакции 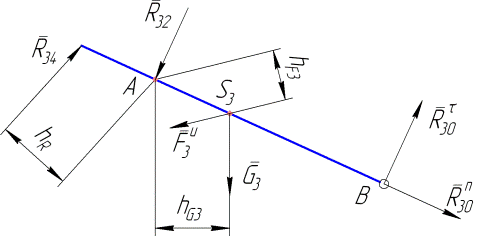
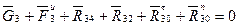 (4.7)
(4.7)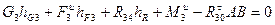 (4.8)
(4.8)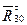 и получаем модуль одной из неизвестных векторного уравнения (4.3). Модули реакций
и получаем модуль одной из неизвестных векторного уравнения (4.3). Модули реакций 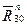 и
и 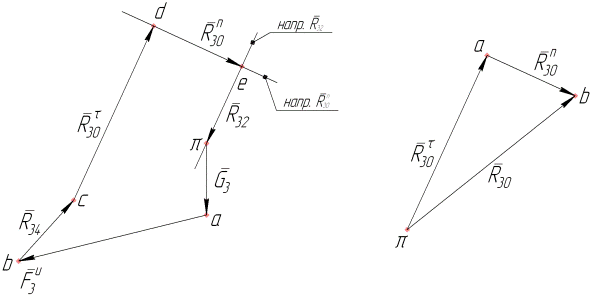
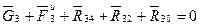 (4.9)
(4.9)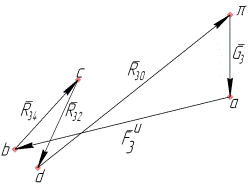
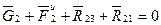 и ищем его графическое решение (см. рис. 4.17).
и ищем его графическое решение (см. рис. 4.17).