
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики (особенности) сигналов
Cреди сигналов, 1. Аналоговые непрерывные сигналы. 2. Цифровые (дискретные) сигналы. 3. Случайные сигналы (чаще всего – это помехи).
Аналоговые сигналы Математические модели сообщений, сигналов и помех Общая теория ортогональных разложений
Что такое сигнал: математическая модель сигнала представляет собой функциональную зависимость, в котором аргументом является время. Знание математических моделей сигналов даёт возможность сравнивать их между собой, устанавливать тождество и различие и, в конечном счёте, проводить их классификацию. Рассмотрим понятие линейного пространства сигналов Пусть M={S0(t), S1(t), … } есть множество (в общем случае бесконечное) сигналов. Сигналы принято объединять в множество, если они обладают некоторым общим свойством (примеры: 1) всевозможные аналоговые сигналы, отличные от 0 на интервале (t1, t2), 2) прямоугольные импульсы всевозможных амплитуд и одинаковой длительности τи. Задача теории сигналов состоит в исследовании их свойств. Исследование свойств сигналов множества М становится особенно плодотворным, когда удается выражать одни элементы множества, через другие. Но чтобы это делать, следует руководствоваться определенными правилами. Эти правила (аксиомы) нужно ввести. Говорят, что множество М образует вещественное линейное пространство, если для него справедливы следующие аксиомы: 1) любой сигнал S(t) 2) для любых Si(t) а) Sj(t)+Si(t)=Si(t)+Sj(t) – свойство коммутативности, б) (Si(t)+Sj(t))+Sk(t)=Si(t)+(Sj(t)+Sk(t)) – свойство ассоциативности; 3) для любого S(t) Sl(t)=a×S(t) 4) Множество М имеет один особый нулевой элемент 0, такой, что S(t)+0=S(t) для всех S(t) Если допустить в аксиоме 3 умножение на комплексное число, то мы приходим к понятию комплексного линейного пространства.
Координатный базис В линейном пространстве сигналов можно выделить некоторое подмножество сигналов {e0, e1, …}, в котором каждый элемент олицетворяет собой некоторую координатную ось, играя при этом роль некоторой единицы измерения или единичного вектора, вдоль этой координатной оси.
Выделенное подмножество {е0, е1, …}, является весьма полезным, когда входящие в него элементы (векторы) линейно независимы, т.е. равенство Система линейно независимых векторов образует координатный базис в линейном пространстве. Рассматривая сигнал S(t) как вектор в линейном пространстве, его можно представить в виде суммы
где числа {c0, c1, …} являются проекциями оси координат или проекциями S(t) относительно выбранного базиса.
Нормированное линейное пространство Пусть L есть линейное вещественное пространство сигналов. Говорят, что пространство сигналов L является нормированным, если каждому сигналу S(t) 1) норма неотрицательна: ||S||≥0, ||S||=0, когда S=0; 2) для любого числа “а” (оно может быть комплексным) справедливо равенство ||a×S||=|a|×||S||; 3) если Si Норму вещественных сигналов определяют как
для комплексных сигналов здесь (-∞, +∞) – область существования сигнала, но можно и интервал (t1, t2). Квадрат нормы сигнала носит название энергии сигнала: Физическая трактовка: именно такая энергия выделяется в резисторе сопротивлением 1 Ом, если на его зажимах действует напряжение S(t).
Метрическое линейное пространство Линейное пространство сигналов L является метрическим, если каждой паре сигналов Si(t) При этом должны выполнятся следующие аксиомы: 1) d(Si, Sj)>0, d( 2) d(Si, Sj) = d(Sj, Si) – рефлексивность метрики, 3) для любых 3-х сигналов Si(t)
Обычно метрику определяют как норму разности двух сигналов: d(Si, Sj)=||Si-Sj||.
Скалярное произведение сигналов Скалярное произведение двух вещественных сигналов определяется выражениями
(норма сигнала уподобляется модулю вектора), а косинус угла между ними Свойства скалярного произведения: 1) ( 2) (Si, Sj) = (Sj, Si), 3) (a×Si, Sj) = a×(Si, Sj), где а – вещественное число, 4) (Si+Sj, Sl) = (Si, Sl)+ (Sj, Sl).
Линейное нормированное метрическое пространство с введенным скалярным произведением называется вещественным пространством сигналов Гильберта. Если сигналы комплексные, то введя скалярное произведение сигналов как
мы определяем комплексное гильбертово пространство, при этом (Si, Sj) = (Si, Sj)*.
Ортогональные сигналы и обобщенный ряд Фурье Два сигнала называются ортогональными, если их скалярное произведение, а следовательно, и их взаимная энергия = 0:
Если во введенном ранее нами координатном базисе {e0, e1, …} все векторы ортогональны друг другу, то В этом случае говорят, что в линейном нормированном метрическом пространстве задан ортогональный базис. Если при этом подмножество {e0, e1, …} бесконечно, то введенные нами ранее представления сигнала в виде суммы Последнее представление сигнала в виде бесконечного ряда называется обобщенным рядом Фурье. Для нахождения коэффициентов этого ряда обе части умножим на произвольную базисную функцию ej(t) и проинтегрируем по области определения множества сигналов:
так как
Тогда для вещественных сигналов
Для комплексных сигналов
Если множество векторов, образующих ортогональный базис {e0, e1, …}, таково, что эти векторы имеют единичные нормы, т.е.
то говорят, что задан ортонормированный базис. Если ортогональный базис не бесконечен, то говорят не об обобщенном ряде Фурье, а о разложении сигнала S(t) в ряд в заданном ортогональном базисе.
Примеры ортогорнальных базисов
1. Ортогональная система экспоненциальных функций: …, e-j2Ωt, e- jΩt, 1, e jΩt, e j2Ωt, … Функции ортогональны на периоде сигнала Т, при этом Ряд Фурье имеет вид и называется комплексным рядом Фурье. Норма базисных функций имеет вид
Базисные функции ортогональны:
Коэффициенты ряда Фурье:
При этом С использованием этих формул ряд Фурье приводится к виду
Для коэффициентов ряда и фазовых углов имеют место соотношения: | C -n|=| C n|; Ө-n=-Өn. Можно показать (проверить самим), что любая пара слагаемых комплексного ряда Фурье, симметрично расположенных относительно n=0, с использованием этих свойств в сумме дает одно вещественное колебание. При этом из комплексного ряда Фурье следует тригонометрический ряд Фурье в виде
Известна другая форма записи тригонометрического ряда Фурье:
где Сравнивая оба ряда видим, что
или
2. Тригонометрическому ряду Фурье соответствует ортогональная система тригонометрических функций (эта система приведена в книге [1] И.С.Гоноровского “Радиотехнические цепи и сигналы”, 1986 г.): 1, cosΩt, sinΩt, cos2Ωt, sin2Ωt, … Интервал ортогональности тот же: Квадраты нормы базисных функций имеют вид
Выбранную ортогональную систему тригонометрических функций можно сделать ортонормированной, если в сами функции ввести поправочные коэффициенты, чтобы нормы функций были = 1 (эта система приведена в книге [2] С.И. Баскакова “Радиотехнические цепи и сигналы”, 1983 г.):
Замечание: 1) Совокупность коэффициентов | C n| комплексного ряда Фурье с учетом их зависимости от частоты есть амплитудно-частотный спектр сигнала (АЧС):
Рис.1. Амлитудно-частотный спектр сигнала
2) Зависимость фазы членов ряда Фурье от частоты есть фазо-частотная характеристика сигнала (ФЧС). Строится для конкретного сигнала:
Рис.2. Фазо-частотный спектр сигнала
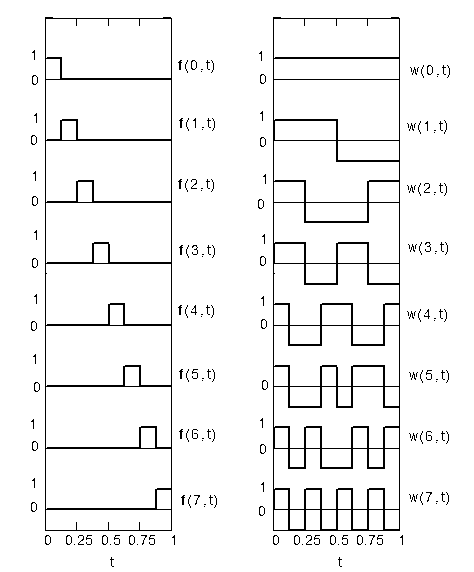
3. Ортонормированная система функций Уолша. Ниже на рисунке в колонке справа приведены 8 первых функций Уолша.
4. Мультипликативно-ортогональный базис. Ниже на рисунке в колонке слева приведены 8 первых функций этого базиса.
Рис.3. Мультипликативно-ортогональный базис (слева) и базис функций УОЛША
Нетрудно убедиться в том, что все базисные функции ортогональны. В настоящее время известно достаточно большое число ортогональных базисов. Так, для представления непрерывных сигналов часто используются ортогональные полиномы и функции Лежандра, Чебышева, Лагерра, Эрмита и т.д.
1. Полиномы Лежандра (первого рода) определяются по формуле:
Они ортогональны на интервале (-1, +1). При n-целом полиномы содержат конечное число членов.
2. Полиномы Чебышева (первого рода) определяются по формуле:
Полиномы Чебышева ортогональны с весом "
3. Полиномы и функции Лагерра определяются формулами:
Эти полиномы ортогональны на полуоси 0<x<∞ с весом “ Так как полиномы Лагерра расходящиеся, то удобно пользоваться функциями Лагерра
4. Полиномы Эрмита определяются формулой
Они ортогональны на всей оси (-∞,∞) с весом
Более подробно см. [1] Гоноровский И.С. Радиотехнические цепи и сигналы, 1986, гл.14.
Замечание. 1. Среди разнообразных систем ортогональных функций, используемых для представления сигналов, исключительно важное место занимают гармонические функции. Почему? Дело в том, что есть два фактора, определяющие эти свойства. 1) Эти функции технически реализуются наиболее простым способом.
2) Они не изменяют свою форму при прохождении через линейные цепи, изменяются лишь амплитуда и начальная фаза. Раздел теории сигналов, в котором для представления сигналов используются исключительно гармонические функции с различными частотами, называется спектральным представлением сигналов или спектральным разложением сигналов. Представление сигналов в виде рядов по другим системам ортогональных функций носит название «временного представления сигналов».
В технической литературе можно встретить использование ряда Фурье для спектрального представления непериодического сигнала. Суть здесь в следующем. Пусть задан сигнал S(t) на интервале (t1,t2). Чтобы разложить его в ряд Фурье его следует сделать сначала периодическим с некоторым произвольно выбранным периодом Т, а затем разложить в ряд Фурье по уже известным правилам.
Рис.4. Преобразование непериодического сигнала в периодический
От выбранного периода Т будет зависеть вид спектра. Лекция 2
|
||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.89.85 (0.102 с.) |
 участвующих в определении электромагнитной обстановки в настоящее время, принимают участие три вида:
участвующих в определении электромагнитной обстановки в настоящее время, принимают участие три вида: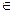 M при любых t принимает вещественные значения;
M при любых t принимает вещественные значения;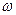 (t)
(t) 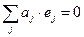 справедливо лишь в том случае, когда одновременно все aj=0.
справедливо лишь в том случае, когда одновременно все aj=0.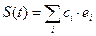 ,
, 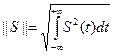 или
или 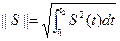 ,
,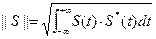 ,
,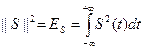 .
. ,
, 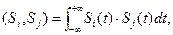
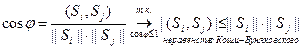 .
. ,
,
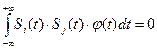 – ортогональность с весом
– ортогональность с весом 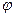 (t).
(t).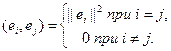
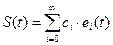 .
.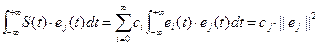 ,
,
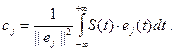
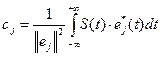 .
.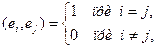
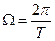 .
.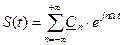
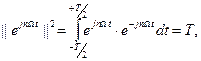
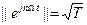 для всех n.
для всех n. =0,
=0, .
.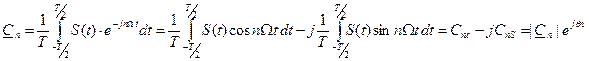 .
.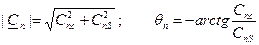 .
.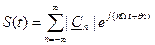 .
.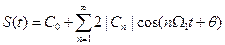 .
.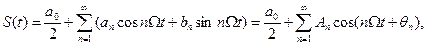
 .
.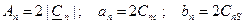 ;
;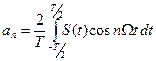 ;
; 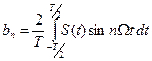 , для всех n≥0.
, для всех n≥0.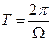 .
.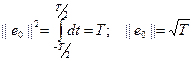 ;
;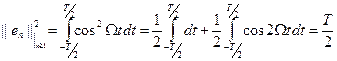 .
.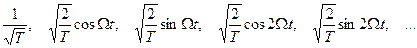

 ,
,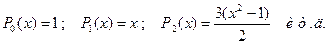
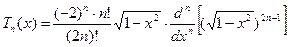 .
.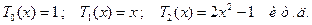
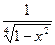 " на интервале (-1, 1):
" на интервале (-1, 1):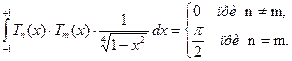
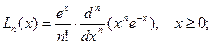
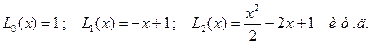
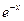 ”.
”.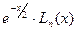 , которые ортогональны свесом =1.
, которые ортогональны свесом =1.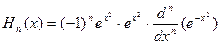 .
.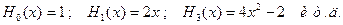
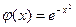 :
: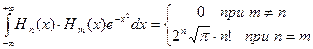 .
.



