
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема7. Использование игровых методовСодержание книги
Поиск на нашем сайте
ПРИ ПРИНЯТИИ РЕШЕНИЙ Понятие об игровых методах Одним из методов принятия решений в условиях дефицита информации, риска и неопределенности является использование теории игр и статистических решений. Игра – это упрощенная, очищенная от мелочей модель рыночной, производственной или другой ситуации. В игре задействованы стороны (две или несколько). Рассматриваются (воспроизводятся) их возможные стратегии. Стратегия – это совокупность правил, предписывающих выполнение определенных действий в зависимости от ситуации, сложившейся в ходе игры. Ира называется парной или множественной в зависимости от числа участвующих в ней. Различают игры конфликтные (антагонистические) и игры с "природой". В конфликтных играх (конкуренция, спот, военные действия) стороны осмысленно противодействуют друг другу. Выигрыш одной означает проигрыш другой. Игры с "ПРИРОДОЙ" применяются при изучении производственных ситуаций (организационных, технических и технологических). Поэтому их чаще называют играми с производством. В играх с природой (производством) обычно рассматриваются стороны: 1 организаторы производства (активная сторона А) и 2 совокупность случайных производственных или рыночных ситуаций ("природа") П.. Смысл игры состоит в следующем: 1. Активная сторона должна выбрать такую стратегию (принять решение), чтобы получить максимальный эффект 2. "Природа" (складывающиеся производственные ситуации) активно и осмысленно не препятствуют этому. Но точное состояние "природы" после действия активной стороне неизвестно. 3.Принятие решений игровыми методами основывается на определенных правилах, которые регламентируют действия сторон: наличие и объём информации каждой из сторон о поведении другой; результат игры и др. 4.В процессе игры сторона А (или стороны) оценивают информацию, принимают решения, делают ходы, т.е. предпринимают действия по изменению ситуации в свою пользу. Ходы бывают: 1 личные – это сознательный выбор из возможных вариантов действий, 2 случайные - это выбор из ряда возможных вариантов, определяемых механизмом вероятностного отбора; 3 смешанные – это комбинация личных и случайных
Принятие решений в условиях риска. Используя понятие целевой функции, задача выбора решения в условиях риска формулируется так: при заданных условиях an и действии внешних факторов zk вероятность появления которыхизвестн а, найти элементы решений xm по возможности обеспечивающих полуение экстремальных значений целевой функции.
Каждая операция оценивается ее эффективностью, т.е. вкладом в достижение цели. В общем случае показатель эффективности - ЦЕЛЕВАЯ ФУНКЦИЯ. Целевая функция зависит от трех групп факторов или подсистем. Первая группа а – характеризует такие условия выполнения операции, которые заданы и не могут быть изменены в ходе ее выполнения. Вторая группа Х - может меняться при управлении, влияя на целевую функцию. Эти факторы называют ЭЛЕМЕНАМИ РЕШЕНИЯ. Их выбирают из дерева систем. Третья группа Z – заранее неизвестные условия. Их влияние неизвестно или не изучено.
7.3. Примерпринятия решения в условиях риска Определить оптимальный запас агрегатов на складе ремонтного завода. Определение сторон в игре. - Производство (П), которое в заданных условиях и в случайном порядке «выдает» то или иное требование на замену (ремонт) агрегатов определенного наименования. - организаторы производства (А) в данном случае это организаторы складского хозяйства, которые формируют запас агрегатов. Следовательно, имеем вариант парной игры с ПРИРОДОЙ 2). Идентификация групп факторов целевой функции: an –заданные условия (размер парка, тип, состояние и условия эксплуатации машин, состояние производственно технической базы, квалификация персонала; Эта группа факторов определяет поток требований на ремонт, а так же пропускную способность завода и стоимость самого ремонта. Zk - число требований на ремонт или замену агрегатов, вероятность которого известна заранее; Xm – количество запасных агрегатов на складе. (Которое должно быть по решению организаторов производства). 3).-Определение вероятности появления потребности в ремонте (замене) определенного числа агрегатов qj Ее можно определить: а) расчетом по данным о надежности агрегатов. Вероятность числа требований k = 1, 2, 3…за время t определяется по формуле
Пуассона Где ɷ - параметр потока требований ɷ = При расчете, когда t = 1 (одна смена) формула упрощается:
Где а- среднее число требований на ремонт (замену), приходящееся на одну смену. Например, при а = 3: Вероятность того, что требований в течение смены не будет вообще Р0 = Что будет одно требование Р1 = 0,15; Два требования Р2 = 0,22; три Р 3 =0,22; четыре Р4 = 0,16 и т.д. б) На основании отчетных данных о требованиях на ремонт данного агрегата. При этом, за определенное число смен (например С = 100) собирают сведения о числе требований на ремонт: С1 – число смен, когда требований не было; С2 – число смен с одним требованием; С3 – число смен с двумя требованиями и т.д. Частость, или эмпирическая вероятность, которую можно использовать в игре. ɷ1 = В данном случае при ремонте ежесменно требуется не более 4 агрегатов (по собранным данным). Вероятность того, что: агрегаты вообще не потребуются, равна q1 = 0,1; что потребуется 1 агрегат q2 = 0,4; два – q3 = 0,3; три q4 = 0,1; четыре q5 = 0,1.
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.163.23 (0.011 с.) |

 , где х – средняя наработка на отказ, фиксированный данным требованием.
, где х – средняя наработка на отказ, фиксированный данным требованием.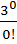 · е-3 =
· е-3 =  · 0,05 = 0,05.
· 0,05 = 0,05.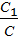 ≈ Р1
≈ Р1


