
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II . Определение плотности жидкостиСодержание книги
Поиск на нашем сайте Используя сделанные выше рассуждения, выведете формулу для определения плотности жидкости. Массы пустого пикнометра М п и пикнометра с водой М пв возьмем из предыдущих опытов. Масса воды в пикнометре m в = Мпв – Мп (7.2) Обозначим через М ж массу пикнометра с исследуемой жидкостью, тогда по аналогии с (7.2), масса исследуемой жидкости: m ж = М ж - М п. Используем формулу (6.1), откуда объём воды: V в =
Выполнение работы Заполните пикнометр исследуемой жидкостью до метки, взвесьте и занесите в таблицу значение М ж. Опыт повторить трижды. Таблица 2
Примечание: значения М п и Мпв взять из первого опыта.
РАБОТА № 8. ОПЫТНОЕ ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА Актуальность работы: Коэффициент Пуассона – это отношение теплоёмкости газа при постоянном давлении к теплоёмкости газа при постоянном объёме. Эта величина зависит от числа степеней свободы газа и является одной из характеристик газа. Цель работы: Определение отношения теплоемкостей газа (коэффициент Пуассона) методом Клемана-Дезорма. Целевые задачи: знать: уравнение Менделеева-Клайперона, изопроцессы, определение теплоёмкости, теплоёмкости газов в любом изопроцессе уметь: определять отношения теплоемкостей газа (коэффициент Пуассона) методом Клемана-Дезорма. План подготовки конспекта: 1. Основные теоретические сведения 2. Выяснить, что измеряется в лабораторной работе, каким методом и для чего. 2. Подготовить таблицу. 3. Записать расчётную формулу. Вопросы для подготовки к входному тестированию: 1. Первое начало термодинамики. 2. Удельная теплоемкость. Связь между удельными теплоемкостями. 3. Молярная теплоемкость при постоянном объеме. 4. Молярная теплоемкость при постоянном давлении. 5. Почему Cp, больше Cv? 6. Какой процесс называется адиабатическим? 7. Что происходит с внутренней энергией газа и его температурой при адиабатическом расширении, при адиабатическом сжатии? 8. Чему равна внутренняя энергия газа? 9. В какой момент вашей работы происходит адиабатический процесс, изохорический процесс, объясните на графике. 10. Почему кран открывается на короткий промежуток времени? 11. Какие значения принимает i для 1, 2 и 3 атомных газов. 12. Какое влияние на результат опыта окажет присутствие водяного пара.
Теоретические сведения Любое состояние газа можно характеризовать тремя основными параметрами: давлением (Р), объемом (V) и температурой (Т). Уравнение, которое связывает эти параметры, называется уравнением состояния газа. Таким уравнением для идеального газа является уравнение Менделеева – Клапейрона: PV=nRT, где n – число молей в объеме V. Зная массу газа и его молекулярный вес m, можно определить число молей n, содержащихся в этом объеме:
Для одного моля n = 1 уравнение имеет вид: PV=RT, (8.2) где R – универсальная газовая постоянная, ее численное значение определяется соотношением: R = где P0 = 1атм., V 0 = 22,4 литра (это объем, занимаемый одним молем газа при Т0 = 2730 К). В системе СИ R = 8,31 . 103 дж/кмоль×градус. В калориях R» 2 кал/моль×градус. Теплоемкость газа зависит от условий нагревания газа. Удельная теплоемкость газа c - количество тепла, которое необходимо подвести к единице массы вещества, чтобы повысить его температуру на один градус. Ее можно определить, воспользовавшись выражением: DQ= сm DТ, откуда с = Молярная теплоемкость «C» - количество тепла, которое необходимо подвести к одному молю вещества, чтобы повысить его температуру на один градус. Она связана с удельной теплоемкостью соотношением: С = Чтобы определить значение теплоемкости в разных процессах, воспользуемся первым началом термодинамики. 1-е начало термодинамики. Теплота, подводимая к газу, расходуется на увеличение внутренней энергии газа U и на работу совершаемую газом против внешних сил. D Q= D U+ A (8.5) (5) Внутренняя энергия идеального газа равна: U = где i - число степеней свободы молекулы газа. Эта величина отражает количество координат характеризующих положение частицы в пространстве. Ее изменение равно D U = Внутренняя энергия газа изменяется при изменении температуры газа. Элементарная работа, совершаемая газом, равна: D A=P D V или dА =PdV (8.8) (8) В формулу, определяющую молярную теплоемкость (8.4), подставим выражение (8.5): C= Пользуясь этой формулой, можно определить теплоемкость газа в любом процессе. Изохорический процесс
Процесс называется изохорическим, если объем газа остается постоянным: V=const, поэтому V2=V1 и изменение DV=0. Работа равна DA=P DV=0 В изохорическом процессе работа не совершается, все тепло, подводимое к газу, идет на увеличение его внутренней энергии. 1-е начало термодинамики для этого процесса принимает вид:
Молярная теплоемкость в этом процессе равна: C v = Подставив вместо DU выражение (7.7), получим значение теплоемкости при постоянном объеме: C v = (10) Изобарический процесс Процесс называется изобарическим, если давление газа остается постоянным (P=const). В этом процессе и объем газа и его температура изменяются, следовательно, тепло, подведенное к газу, расходуется и на работу и на увеличение внутренней энергии газа. Молярная теплоемкость газа в этом процессе определяется соотношением: C р= Подставив вместо DU выражение (7.7), а вместо D А = P DV = С р= Теплоемкость при постоянном давлении больше, чем теплоемкость при постоянном объеме, так как в этом процессе подведенное тепло идет не только на увеличение внутренней энергии газа, но и на работу, совершаемую газом против внешних сил.
Изотермический процесс Процесс, протекающий при постоянной температуре, называется изотермическим (T=const). В этом процессе DT=0, следовательно, внутренняя энергия газа не изменяется DU=0. Все тепло, подводимое к газу, расходуется на работу: ΔQ=ΔA Теплоемкость в этом процессе равна CT = В этом процессе газ ведет себя как тело, обладающее бесконечно большой теплоемкостью. Сколько бы тепла к нему не подводилось, его температура не изменяется.
Адиабатический процесс Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим: ΔQ=0, тогда 0=ΔU+ΔA, ΔA= - ΔU. В этом процессе газ совершает работу за счет уменьшения своей внутренней энергии, при этом температура газа понижается. Если - ΔА=ΔU, затраченная работа идет на увеличение внутренней энергии газа, его температура повышается. Теплоемкость в адиабатическом процессе равна: C ад= Большое практическое значение имеет отношение теплоемкостей газа: где γ – коэффициент Пуассона. Эта величина зависит от числа степеней свободы и для разных газов может быть определена опытным путем. Напомним, что i - число степеней свободы - число независимых координат, однозначно характеризующих положение молекулы в пространстве; i=3 - для одноатомного газа, i=5 - для двухатомного газа, i=6 - для многоатомного газа. Определив γ можно рассчитать работу адиабатического процесса, которая равна: A ад= где P 1 и V 1 – давление и объем газа в начальном состоянии; Р 2 и V 2 – давление и объем газа в конечном состоянии. Кроме этого, определив γ и измерив С р, можно рассчитать величину Cv= Целью настоящей работы является определение отношение теплоемкостей газа:
Для этого используется метод Клемана-Дезорма.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.007 с.) |

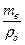 , а объём исследуемой жидкости:
, а объём исследуемой жидкости: 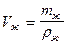 . Так как объёмы воды и исследуемой жидкости равны V в = V ж , то:
. Так как объёмы воды и исследуемой жидкости равны V в = V ж , то: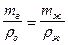 и
и 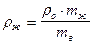 .
.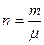 , тогда
, тогда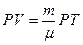 . (8.1)
. (8.1)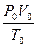 ,
,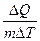 . (8.3) (3)
. (8.3) (3)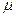 с, С =
с, С = 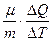 . (8.4) (4)
. (8.4) (4)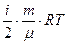 , (8.6) (6)
, (8.6) (6)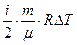 (8.7) (7)
(8.7) (7)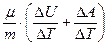 (8.9)
(8.9) DQ= DU
DQ= DU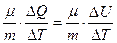
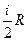
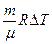 и воспользовавшись соотношением Менделеева-Клайперона, получим для одного моля газа:
и воспользовавшись соотношением Менделеева-Клайперона, получим для одного моля газа: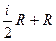 или С р =С v +R (11)
или С р =С v +R (11)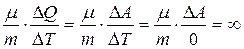
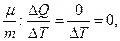 С ад = 0
С ад = 0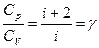 ,
, 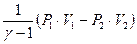 ,
, для данного газа, которую определить опытным путем очень сложно.
для данного газа, которую определить опытным путем очень сложно.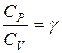 . (7.10)
. (7.10)


