
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы метода измерения поверхностного натяжения жидкостиСодержание книги
Поиск на нашем сайте
Молекулы поверхностного слоя обладают, как указывалось, повышенной потенциальной энергией. Поэтому всякое изменение площади поверхности жидкости связано с совершением работы. Если поверхность жидкости уменьшается, то работу совершает жидкость. Если, наоборот, площадь поверхности возрастает, значит, совершена работа внешних сил над жидкостью. Очевидно, что совершенная работа численно равна изменению поверхностной энергии, которое, в свою очередь, пропорционально изменению площади поверхности жидкости. Если изменение поверхностной энергии обозначить через Коэффициент пропорциональности т.е. коэффициент поверхностного натяжения равен изменению поверхностной энергии при изменении площади поверхности жидкости на единицу. Иначе говоря, коэффициент поверхностного натяжения равен работе, которую нужно совершить для увеличения площади поверхности жидкости на единицу, или работе, которую совершает поверхностный слой при ее уменьшении на единицу. Благодаря тому, что силы, действующие на поверхностный слой жидкости, стремятся уменьшить площадь ее поверхности, жидкости ведут себя так, как будто бы их поверхности представляют собой тонкие упругие "натянутые" пленки. Многие опыты, например, с мыльными пузырями, жидкими пленками, "натянутыми" на проволочные каркасы, такие явления, как образование пены и др., свидетельствуют об этом. Разумеется, никакой особой упругой пленки на поверхности жидкости в действительности не существует. Реально существуют поверхностные молекулы, на которые действуют силы, направленные внутрь жидкости. Но именно поэтому можно считать, что на поверхности жидкости действуют силы, касательные к ней и перпендикулярные к любой линии, взятой на поверхности, и к любой линии, составляющей границу между поверхностью жидкости и твердым телом (линии раздела). Поэтому для любой линии, проведенной на поверхности жидкости или являющейся границей между нею и твердым телом, можно написать равенство
где С этой точки зрения коэффициент поверхностного натяжения представляет собой силу, действующую на единицу длины произвольной линии на поверхности жидкости. Из равенств (1.1) и (1.3) видно, что размерность коэффициента поверхностного натяжения или Дж/м2, или Н/м. Легко убедиться в том, что равенство (1.3) непосредственно следует из (1.1). Если, например, некоторая поверхность жидкости С другой стороны, сила Но Если кольцо, изготовленное из материала, который смачивается исследуемой жидкостью, отрывать от контактирующей с ним жидкости, то можно считать, что отрыв происходит по двум линиям - внешней и внутренней окружности кольца. Если внешний диаметр кольца равен Отсюда, зная Это и есть основная расчетная формула, используемая в данной работе.
|
|||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.194 (0.01 с.) |


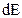
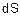 , то можно написать
, то можно написать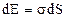
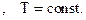 . (1.1)
. (1.1)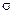 , входящий в эту формулу,
, входящий в эту формулу, 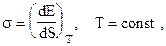

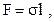 (1.3)
(1.3)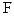 - сила, действующая на линию,
- сила, действующая на линию, 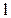 - ее длина.
- ее длина.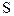 увеличилась из-за того, что под действием силы
увеличилась из-за того, что под действием силы 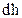 , то потенциальная энергия поверхностного слоя увеличилась на
, то потенциальная энергия поверхностного слоя увеличилась на 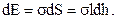 (1.4)
(1.4) , равную
, равную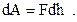 (1.5)
(1.5)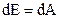 . Отсюда
. Отсюда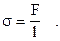 (1.6)
(1.6)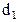 , а внутренний
, а внутренний 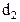 , то сила, удерживающая жидкость у кольца, согласно (1.3), равна
, то сила, удерживающая жидкость у кольца, согласно (1.3), равна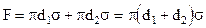 . (1.7)
. (1.7)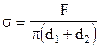 . (1.8)
. (1.8)


