Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная погрешность прямых измеренийСодержание книги
Поиск на нашем сайте
Результат любого измерения содержит некоторую ошибку, которая обусловлена систематическими ошибками измерительных приборов. Допустим, что в результате измерения некоторой величины х получены следующие значения х1, х2, х3,... хn (частота появления значений х не учитывается, если количество измерений n < 30). Результат измерения определяется как среднее арифметическое наблюдаемых значений:
Абсолютная погрешность измерения
где
где
Относительная погрешность прямых измерений Относительная погрешность прямых измерений (Е %) вычисляется по формуле: Е % = где По значению относительной погрешности можно судить о качестве измерений. Если: Е % 1% < E % Е % > 5 % - качество неудовлетворительное. Абсолютная погрешность косвенных измерений функции одной Переменной Абсолютная погрешность косвенных измерений функции одной переменной U= f (х) вычисляется по формуле [3]:
где Абсолютная погрешность может быть получена из опыта, либо найдена путем вычислений. При работе с измерительными приборами
Абсолютная погрешность косвенных измерений функции Нескольких переменных Рассмотрим функцию двух переменных U= f (х, y). Абсолютная погрешность определяется:
где
1.5. Доверительный интервал Запись истинного значения косвенных измерений находящихся в интервале:
Относительная погрешность рассчитывается по формуле:
Запись результатов Абсолютная погрешность округляется до двух значимых цифр взятых с избытком. Значимыми называются цифры отличные от нуля, кроме нуля стоящего между двумя другими цифрами. В окончательный результат заносятся все известные цифры, кроме сомнительных цифр (вместо сомнительной цифры записывается 0). Сомнительными называются цифры, имеющие тот же порядок, что и округленная цифра в абсолютной погрешности и все остальные, следующие за ней цифры. Пример округления: U =26,152; f = 3,412; После округления: U Пример вычисления погрешностей прямых измерений При определении концентрации окрашенного раствора колориметром Дюбоска получены следующие значения толщины слоя жидкости: 10,4; 10,6; 10,4; 10,5; 10,7; 10,6; 10,4.
Выполним вычисления и заполним таблицу 1.1 Таблица 1.1 Экспериментальные и расчетные данные
Рассчитаем среднее арифметическое наблюдаемых значений по формуле:
Вычислим оценку средней квадратической погрешности среднего арифметического по формуле (1.1):
Абсолютная погрешность (1.5): Доверительный интервал определим по формуле (1.7):
Оценим качество измерений: E % = Пример расчета доверительного интервала В результате проведенных измерений тока и напряжения, для построения вольтамперной характеристики полупроводникового диода, были получены следующие данные: при изменении напряжения на диоде от 0,8 до 6,0 вольт, величина прямого тока (Iпр) изменилась от 6 до 200 миллиампер (см. табл. 1.2).
Таблица 1.2 Результаты измерений напряжения и тока
В данном примере для нас представляет интерес зависимость сопротивления диода от напряжения при протекании прямого тока. Величину сопротивления диода для прямого тока вычислим по закону Ома:
где
В данном случае за абсолютную погрешность можно приять систематическую погрешность приборов, которая равняется половине цены деления прибора.
Значения сопротивлений: R1 R2 R3 R4 R5 R6
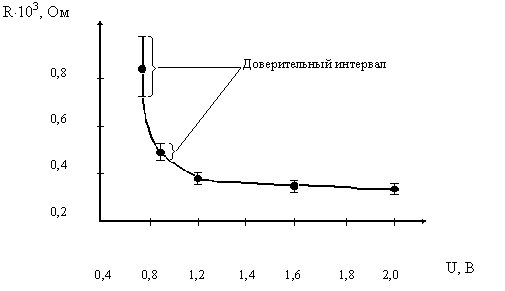
Далее, по этим данным строится график зависимости сопротивления диода от величины напряжения с указанием на графике доверительных интервалов (рис.1.1). Рис. 1.1 Зависимость сопротивления диода от величины напряжения
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.44 (0.008 с.) |

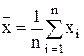 . (1.1)
. (1.1)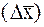 вычисляется по формуле [3]:
вычисляется по формуле [3]: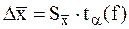 , (1.2)
, (1.2)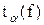 - коэффициент Стьюдента; f= n-1 - число степеней свободы;
- коэффициент Стьюдента; f= n-1 - число степеней свободы;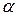 - доверительная вероятность.
- доверительная вероятность.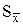 - оценка средней квадратической погрешности среднего арифметического находится, как [2]:
- оценка средней квадратической погрешности среднего арифметического находится, как [2]: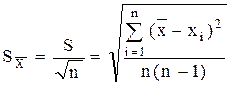 , (1.3)
, (1.3)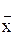 - среднее арифметическое проведенных измерений, определяемое по формуле (1.1).
- среднее арифметическое проведенных измерений, определяемое по формуле (1.1). ; (1.4)
; (1.4) - абсолютная погрешность.
- абсолютная погрешность.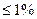 - качество измерений хорошее;
- качество измерений хорошее;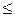 5 % - качество удовлетворительное;
5 % - качество удовлетворительное;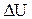 =
= 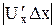 , (1.5)
, (1.5)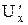 - первая производная по х;
- первая производная по х; 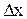 - абсолютная погрешность прямых измерений определяемая по формуле (1.2).
- абсолютная погрешность прямых измерений определяемая по формуле (1.2). , (1.6)
, (1.6)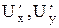 - частные производные U= f (x, y) по переменным х и y соответственно;
- частные производные U= f (x, y) по переменным х и y соответственно; 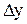 - абсолютные погрешности прямых измерений.
- абсолютные погрешности прямых измерений. или (U
или (U 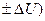 (1.7)
(1.7)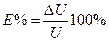 . (1.8)
. (1.8)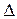 f= 0,02063.
f= 0,02063.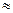 0,24;
0,24; 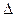 f это округленные цифры, то цифра 5 в U и цифра 2 в f сомнительные. Тогда окончательный результат U и f запишется как:
f это округленные цифры, то цифра 5 в U и цифра 2 в f сомнительные. Тогда окончательный результат U и f запишется как: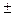 0, 24); f
0, 24); f 
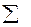
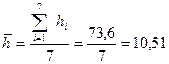 ;
;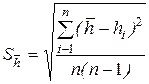 =
= 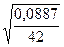 = 0,046;
= 0,046;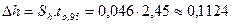 ; После округления запишем:
; После округления запишем: 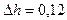 .
.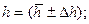 h = (10,50
h = (10,50 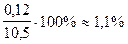 - качество измерений удовлетворительное.
- качество измерений удовлетворительное.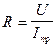 . Величина R является косвенно измеряемой величиной, так как рассчитывается по формуле, в которую входят результаты прямых измерений. Абсолютная погрешность
. Величина R является косвенно измеряемой величиной, так как рассчитывается по формуле, в которую входят результаты прямых измерений. Абсолютная погрешность 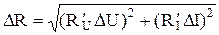 ,
,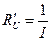 - частная производная по переменной U;
- частная производная по переменной U;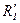
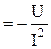 - частная производная по переменной I.
- частная производная по переменной I.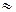 0,133·103;
0,133·103; 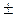 0,056);
0,056);