
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел I . Линейная алгебра.
1. Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц. 2. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц. 3. Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей. 4. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца. 5. Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ. 6. Решение, множество решений, совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство. 7. Теорема Крамера (о разрешимости СЛУ порядка 8. Метод Гаусса решения СЛУ, условия его применимости. Условия несовместности, определённости и неопределённости СЛУ по методу Гаусса. 9. Преобразования СЛУ, выполняемые при выполнении прямого и обратного ходов метода Гаусса. Базисные и свободные переменные. Нахождение общего решения СЛУ. Частные решения СЛУ. 10. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы. 11. Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости. 12. Однородные СЛУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛУ. 13. Минор 14. Понятие 15. Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов. 16. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.
17. Понятие векторного пространства 18. Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение оператора на оператор, обратный оператор. 19. Понятие собственного числа и собственного вектора оператора. Характеристическое уравнение. Нахождение собственных чисел и векторов оператора. 20. Понятие квадратичной формы. Матрица квадратичной формы. Вырожденная, невырожденная, каноническая квадратичная форма. Закон инерции квадратичных форм. 21. Понятие знакоопределённости квадратичной формы. Главные миноры. Критерии знакоопределённости квадратичной формы.
Раздел II. Векторная алгебра. 22. Понятие геометрического вектора. Равенство векторов. Противоположный вектор. Орт вектора. Графические правила сложения, вычитания, умножения вектора на число. Проекция вектора на вектор. 23. Коллинеарность и компланарность векторов. Базис и канонический базис плоскости 24. Понятие декартовой системы координат в 25. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты векторов. Вычисление угла между векторами. Условие ортогональности векторов. 26. Векторное произведение векторов, его геометрический смысл и свойства. Выражение векторного произведения через координаты векторов. Условие коллинеарности векторов. 27. Смешанное произведение векторов, его геометрический смысл и свойства. Выражение смешанного произведения через координаты векторов. Условие компланарности векторов.
Раздел III. Аналитическая геометрия. 28. Понятие линии на плоскости. Общее уравнение линии и его нахождение по известному геометрическому свойству её точек. Окружность и её уравнение. 29. Прямая линия на плоскости и её общее уравнение. Нормальный и направляющий векторы прямой. Нахождение уравнения прямой, проходящей через точку перпендикулярно вектору. Построение прямой. 30. Каноническое уравнение прямой; уравнение прямой, проходящей через две точки; уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках. Расстояние от точки до прямой на плоскости. Угол между прямыми на плоскости и его вычисление, условия 31. Понятие поверхности. Общее уравнение поверхности, его нахождение по известному геометрическому свойству её точек. Сфера и её уравнение. 32. Плоскость и её общее уравнение. Нормальный вектор плоскости. Уравнение плоскости, проходящей через точку перпендикулярно вектору. Построение плоскости. 33. Уравнение плоскости, проходящей через три точки; уравнение плоскости в отрезках. Расстояние от точки до плоскости. Угол между плоскостями, условия перпендикулярности и параллельности плоскостей. 34. Понятие линии в пространстве и её общее уравнение. Прямая линия в пространстве и её общее уравнение. Направляющий вектор прямой. 35. Уравнения прямой в пространстве: каноническое, проходящей через две точки; параметрическое. Приведение общего уравнения к каноническому. 36. Угол между двумя прямыми в пространстве, между прямой и плоскостью и их вычисление, условия перпендикулярности и параллельности двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости. 37. Кривая 2-ого порядка на плоскости и её общее уравнение. Классификация кривых 2-ого порядка. 38. Эллипс. Каноническое уравнение эллипса. Построение эллипса. Вершины, полуоси, фокусы, эксцентриситет, общее геометрическое свойство точек эллипса. 39. Гипербола. Каноническое уравнение гиперболы. Построение гиперболы. Вершины, полуоси, фокусы, эксцентриситет, асимптоты, общее геометрическое свойство точек гиперболы. 40. Парабола. Каноническое уравнение параболы. Построение параболы. Вершина, фокус, эксцентриситет, директриса, общее геометрическое свойство точек параболы. 41. Область решений линейного неравенства, системы линейных неравенств в Приложения. 6.1. Образец решения контрольных задач типового варианта. 1 – 10. Вычислить определитель: а) непосредственным разложением по б) непосредственным разложением по Решение. а) вычисляем определитель разложением по элементам первой строки:
Тогда б) вычисляем определитель непосредственным разложением по элементам второго столбца:
Тогда Ответ: 11-20. Найти матрицу
Решение: 1) Транспонируем матрицу 2) Вычисляем произведение матриц
3) Находим матрицу
4) Находим матрицу
Ответ: 21-30. Найти собственные числа и векторы матрицы Множество собственных чисел матрицы совпадает с множеством корней характеристического уравнения матрицы Решение: 1) Составляем характеристическое уравнение матрицы
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):
Таким образом, собственными числами матрицы 2) Находим собственные векторы матрицы 2.1) Составляем матричное уравнениедля нахождения собственных векторов или
записываем его в виде системы линейных уравнений: 2.2) Составляем матричное уравнениедля нахождения собственных векторов или
записываем его в виде системы линейных уравнений:
Ответ: 31 – 40. Дана система уравнений: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. Решение. А) Метод Крамера. 1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:
2а) Так как 3а) Вычисляем определители
4а) Находим решение: 5а) Выполняем проверку: Ответ: Б) Метод обратной матрицы. 1б) Записываем систему уравнений в матричном виде:
2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:
3б) Так как
4б) Находим обратную матрицу
Тогда 5б) Находим решение:
6б) Выполняем проверку: Ответ: В) Метод Гаусса. 1в) Записываем расширенную матрицу системы:
2в) Выполняем прямой ход метода Гаусса. В результате прямого хода матрица системы
Замечание. Если при выполнение преобразования расширенной матрицы 3в) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 4в) Выполняем проверку: Ответ:
41-50. Найти общее решение для каждой из данных систем методом Гаусса: а) Решение. 1а) Записываем расширенную матрицу системы:
2а) Выполняем прямой ход метода Гаусса.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных
3а) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: Тогда общее решение системы запишется в виде: 4а) Выполняем проверку:
Ответ: б) Решение. 1а) Записываем расширенную матрицу системы:
2а) Выполняем прямой ход метода Гаусса.
Замечание. В результате прямого хода матрица системы Если, при выполнении преобразования расширенной матрицы Для выполнения условия
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных 3б) Выполняем обратный ход метода Гаусса. Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: Тогда общее решение системы запишется в виде:
4б) Выполняем проверку:
Ответ: в) Решение. 1в) Записываем расширенную матрицу системы:
2в) Выполняем прямой ход метода Гаусса.
При выполнении преобразования расширенной матрицы Ответ: Система несовместна. 51 – 60. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра). а) Решение. 1а) Записываем матрицу квадратичной формы: 2а) Проверяем является ли матрица 3а) Вычисляем угловые миноры матрицы Ответ: Квадратичная форма положительно определена. 1б) Записываем матрицу квадратичной формы: 2б) Вычисляем её определитель 3б) Вычисляем угловые миноры матрицы Ответ: Квадратичная форма знакопеременна.
61 – 70. Даны векторы Решение. 1 a). Находимвектор
= 2а) Находимвектор
= 3а) Вычисляем скалярное произведениевекторов
| Поделиться:
| |
 ). Формулы Крамера для решения СЛУ, условия их применимости.
). Формулы Крамера для решения СЛУ, условия их применимости.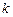 -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).
-ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).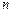 -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число). Линейная комбинация векторов.
-мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число). Линейная комбинация векторов. , евклидова пространства
, евклидова пространства 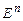 . Базис, канонический базис, ранг
. Базис, канонический базис, ранг 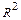 ; базис и канонический базис пространства
; базис и канонический базис пространства  . Координаты вектора.
. Координаты вектора. и ½½ прямых.
и ½½ прямых. . Графическое изображение области решений системы линейных неравенств в
. Графическое изображение области решений системы линейных неравенств в 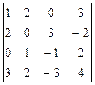
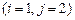
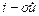 строке;
строке; столбцу;
столбцу;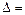
 .
.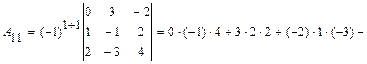
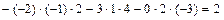
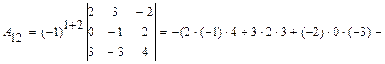
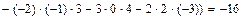

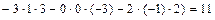
 =
= 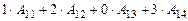 =
= 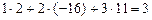
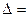
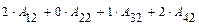 .
.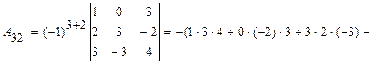
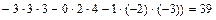
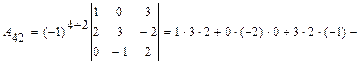
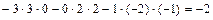
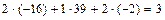 .
. .
. , если:
, если: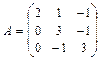 ,
, 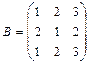 .
. :
: 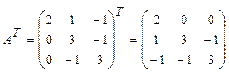 .
.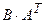 :
: 
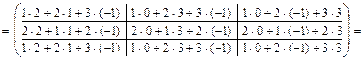
 .
. :
: 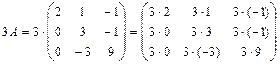
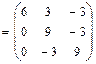 .
.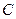 :
: 
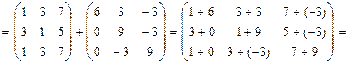
 .
.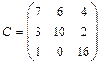 .
.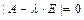 , а множество собственных векторов, отвечающих собственному числу
, а множество собственных векторов, отвечающих собственному числу 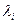 , совпадает с множеством ненулевых решений матричного уравнения:
, совпадает с множеством ненулевых решений матричного уравнения:  , определяемым методом Гаусса.
, определяемым методом Гаусса.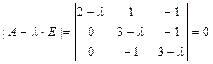 .
.
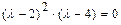
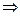
 ,
,  .
. и
и 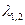 и
и  .
.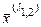 , отвечающих собственному числу
, отвечающих собственному числу 

 ,
,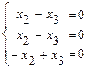 и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе 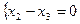 , имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной
, имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной 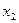 :
:  . Поэтому выбираем в качестве базисной – неизвестную
. Поэтому выбираем в качестве базисной – неизвестную 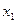 и
и 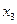 . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения: 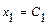 ,
, 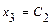 , где
, где 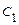 ,
, 
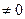 , одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:
, одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов 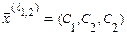 .
. , отвечающих собственному числу
, отвечающих собственному числу 

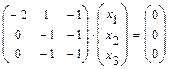 ,
, и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе 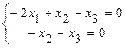 , имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных
, имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные 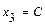 , где
, где 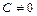 и выражаем через неё значения базисных неизвестных
и выражаем через неё значения базисных неизвестных  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу 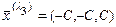 ,
,  . Требуется:
. Требуется:
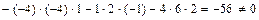 .
. , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: 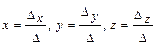
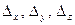 :
: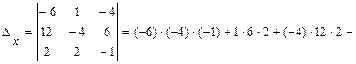
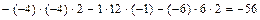 ,
,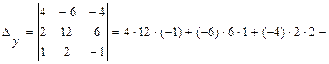
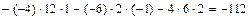 ,
,
 .
. .
.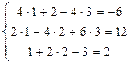
 .
.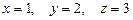 .
.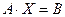 или
или 
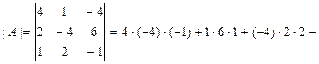
 , то матрица системы
, то матрица системы  и единственное решение системы определяется формулой:
и единственное решение системы определяется формулой:  или
или 
 (методом присоединённой матрицы):
(методом присоединённой матрицы): .
.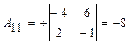
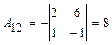



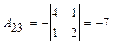
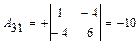


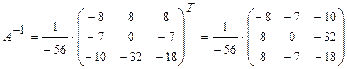 .
.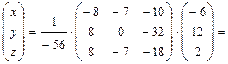
 .
.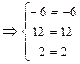 .
.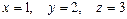 .
. .
. должна быть преобразована с помощью элементарных преобразований строк к матрице
должна быть преобразована с помощью элементарных преобразований строк к матрице 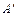 треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами 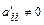 . Система уравнений, матрица которой
. Система уравнений, матрица которой  , имеет единственное решение, а система уравнений, матрица которой
, имеет единственное решение, а система уравнений, матрица которой 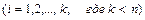 , имеет бесконечно много решений.
, имеет бесконечно много решений.


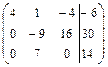

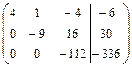 . В результате элементарных преобразований матрица
. В результате элементарных преобразований матрица  . Система уравнений, матрица которой
. Система уравнений, матрица которой  в преобразованной матрице
в преобразованной матрице  появляется строка
появляется строка 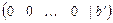 , где
, где 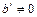 , то это говорит о несовместности исходной системы уравнений.
, то это говорит о несовместности исходной системы уравнений. и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных:
и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных: 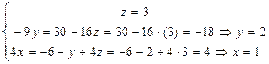 .
. .
. .
.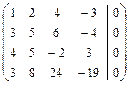

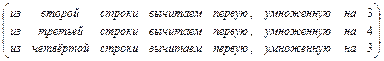
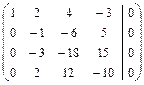
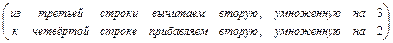
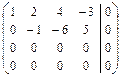
 .
.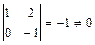 . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  .
.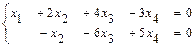 . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
, 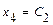 , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: 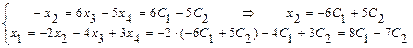 .
. .
.
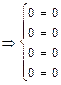 .
. .
.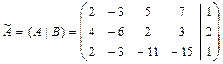 .
.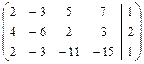


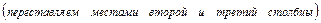
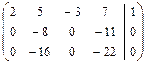
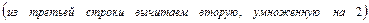


 .
.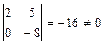 . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные 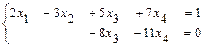 . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения: 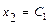 ,
, 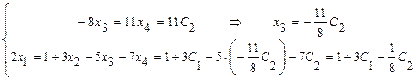 .
. 
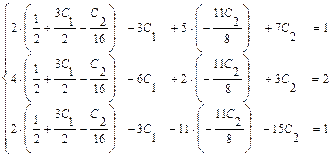
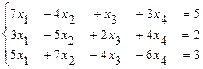 .
.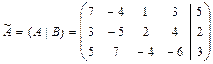 .
.



 .
. , соответствующая уравнению
, соответствующая уравнению 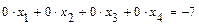 , которому не удовлетворяет ни один набор значений неизвестных
, которому не удовлетворяет ни один набор значений неизвестных  , что говорит о несовместности исходной системы уравнений.
, что говорит о несовместности исходной системы уравнений. ; б)
; б) 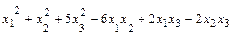
 .
.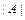 и проверяем, равен ли он нулю:
и проверяем, равен ли он нулю:  . Так как
. Так как 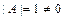 , то матрица
, то матрица  ,
,  ,
, 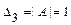 . Так как выполняется условие:
. Так как выполняется условие:  ,
, 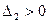 ,
,  , то по критерию Сильвестра квадратичная форма положительно определена.
, то по критерию Сильвестра квадратичная форма положительно определена. .
. . Так как
. Так как  , то матрица
, то матрица  ,
,  . Так как два угловых минора нечётного порядка имеют разные знаки:
. Так как два угловых минора нечётного порядка имеют разные знаки: 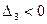 , то по критерию Сильвестра квадратичная форма знакопеременна.
, то по критерию Сильвестра квадратичная форма знакопеременна.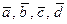 :
:  ;
;  ;
; 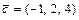 ;
;  . Требуется: а) вычислить скалярное произведение векторов
. Требуется: а) вычислить скалярное произведение векторов 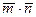 , если
, если 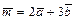 ,
, 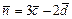 ; б) вычислить векторное произведение векторов
; б) вычислить векторное произведение векторов 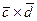 ; в) показать, что векторы
; в) показать, что векторы  образуют базис
образуют базис 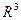 и найти координаты вектора
и найти координаты вектора  в этом базисе.
в этом базисе.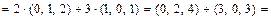
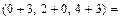
 .
.
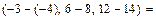
 .
.


