
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учебно-методический комплекс. Учебно-методический комплексСтр 1 из 5Следующая ⇒
ЛИНЕЙНАЯ АЛГЕБРА
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС для студентов заочной формы обучения Г. Набережные Челны 2011 1.Цель и задачи дисциплины, её место в учебном процессе. Цель преподавания дисциплины «Линейная алгебра» -формирование системы базовых знаний по данной дисциплине, которая позволит будущим специалистам решать в своей повседневной деятельности актуальные задачи практики, понимать написанные на современном научном уровне результаты других исследований и тем самым совершенствовать свои профессиональные навыки. Основными задачами дисциплины являются: - ознакомление студентов с ролью математики в современной жизни, с характерными чертами математического метода изучения реальных задач; - обучение студентов теоретическим основам курса; - привитие практических навыков математического моделирования реальных социально-экономических задач с использованием математического аппарата данного курса; - развитие у студентов навыков творческого и логического мышления, повышение общего уровня математической культуры. Данная дисциплина является основой при изучении таких дисциплин, как «Численные методы», «Теория вероятностей и математическая статистика», «Многомерные статистические методы», «Методы оптимизации», «Исследование операций», «Эконометрика», а также других дисциплин, изучающих современные экономико-математические методы. В свою очередь, для изучения данной дисциплины необходимо знание элементарной математики. В результате изучения данной дисциплины студент должен: - знать теоретические основы линейной и векторной алгебры, алгебры многочленов, аналитической геометрии; - уметь использовать полученные знания для решения практических задач. Изучение дисциплины предусматривает проведение лекционных, практических занятий и самостоятельную работу студентов. В лекциях излагается содержание тем программы с учётом требований, установленных для специалиста в квалификационной характеристике. Практические занятия проводятся с целью закрепления теоретических основ курса, получения практических навыков решения математических задач. Контроль знаний осуществляется с помощью контрольной работы и итогового экзамена.
2. Содержание и структура дисциплины. 2.1 Содержание дисциплины (наименование и номера тем). Раздел I. ЛИНЕЙНАЯ АЛГЕБРА. Тема 1. Определители. Определители 2-ого, 3-его, порядков, порядка n. Свойства определителей. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца. Вычисление определителей. Литература: [1] –C.142-154; [2] – C.22-26; [3] – C.426-431; [4] – C.263-268. Тема 2. Матрицы. Определение матрицы. Виды матриц. Действия над матрицами. Линейная зависимость и независимость строк матрицы. Базисный минор. Ранг матрицы. Обратная матрица, условие существования, основные способы её нахождения. Матричные уравнения, их решение. Литература: [1] –C.136-142; 159-165;174-182; [2] – C.9-16; 26-29; [3] – C.416-426; 431-435; [4] – C.259-263; 272-276. Тема 3. Системы линейных уравнений. Системы линейных уравнений (СЛУ). Основные понятия и определения. Матричная запись СЛУ. Теорема Кронеккера-Капелли. Формулы Крамера. Решение СЛУ методом обратной матрицы. Решение СЛУ методом Гаусса. Базисные и свободные неизвестные. Общее, базисное и опорное решения СЛУ. Однородные системы линейных уравнений, свойства их решений. Условия существования ненулевых решений однородных СЛУ. Фундаментальная система решений. Структура общего решения СЛУ. Литература: [1] –C.136-142; 154-159; 165-174; [2] – C.38-53; [3] – C.436-457; [4] – C.268-276.
Тема 5. Линейные операторы. Линейный оператор, действия над ними. Собственные векторы и собственные значения линейных операторов, их свойства и нахождение. Литература: [1] –C.202-221; [2] – C.78-86. Тема 6. Квадратичные формы. Квадратичные формы. Закон инерции квадратичных форм. Положительно и отрицательно определённые квадратичные формы. Критерии знакоопределённости квадратичных форм. Литература: [1] –C.251-261; [2] – C.86-91. Тема 7. Векторная алгебра. Геометрические векторы на прямой, плоскости и в пространстве, действия над ними. Проекция вектора. Прямоугольная декартова система координат. Радиус-вектор. Координаты вектора. Линейные операции над векторами в координатной форме. Длина и направляющие косинусы вектора. Расстояние между точками. Деление отрезка в данном отношении. Скалярное, векторное, смешанное произведения векторов, их свойства, выражение в координатной форме, приложения для решения геометрических задач. Условия перпендикулярности, параллельности и компланарности векторов.
Литература: [1] –C.5-37; [2] – C.63-68; [3] – C.301-305; [4] – C.222-241. Задания для контрольной работы.
1 – 10. Вычислить определитель: а) непосредственным разложением по б) непосредственным разложением по 1. 4. 7. 10. 11 – 20. Найтиматрицу 11. 13. 15. 17. 19. 21 – 30. Найтисобственные числа и собственные векторы матрицы 21. 24. 27. 30.
31 – 40. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. 31. 33. 35. 37. 39. 41–50. Найти общее решение для каждой из данных систем методом Гаусса: 41 а) 42 а) 43. а) 44. а) 45. а) 46. а) 47. а) 48. а) 49. а) 50. а) 51 – 60. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра). 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. 61 – 70. Даны векторы а) вычислить скалярное произведение векторов
61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71-80. Даны вершины треугольника а) длину стороны в) уравнение медианы г) уравнение высоты д) длину 71. 73. 75. 77. 79. 81 – 90. Даны вершины пирамиды а) длины ребер в) площадь грани д) уравнение плоскости грани е) длину 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. 91–100. Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её. 91. 93. 95. 97. 99. 101-110. Требуется: а) изобразить графически область допустимых решений системы неравенств; б) найти графическим способом решение задачи линейного программирования. 101. 104. 107. 109.
111-120. Имеются данные о работе трёх отраслей экономики в отчётном периоде и план выпуска конечной продукции 111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
Вопросы к экзамену. Приложения. 6.1. Образец решения контрольных задач типового варианта. 1 – 10. Вычислить определитель: а) непосредственным разложением по б) непосредственным разложением по Решение. а) вычисляем определитель разложением по элементам первой строки:
Тогда б) вычисляем определитель непосредственным разложением по элементам второго столбца:
Тогда Ответ: 11-20. Найти матрицу
Решение: 1) Транспонируем матрицу 2) Вычисляем произведение матриц
3) Находим матрицу
4) Находим матрицу
Ответ: 21-30. Найти собственные числа и векторы матрицы Множество собственных чисел матрицы совпадает с множеством корней характеристического уравнения матрицы Решение: 1) Составляем характеристическое уравнение матрицы
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):
Таким образом, собственными числами матрицы 2) Находим собственные векторы матрицы 2.1) Составляем матричное уравнениедля нахождения собственных векторов или
записываем его в виде системы линейных уравнений:
2.2) Составляем матричное уравнениедля нахождения собственных векторов или
записываем его в виде системы линейных уравнений: Ответ: 31 – 40. Дана система уравнений: а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса. Решение. А) Метод Крамера. 1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:
2а) Так как 3а) Вычисляем определители
4а) Находим решение: 5а) Выполняем проверку: Ответ: Б) Метод обратной матрицы. 1б) Записываем систему уравнений в матричном виде:
2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:
3б) Так как
4б) Находим обратную матрицу
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 53; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.214.215 (0.219 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
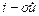 строке;
строке; столбцу.
столбцу. 2.
2. 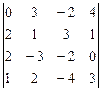 3.
3. 

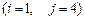
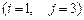
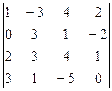 5.
5.  6.
6. 
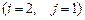


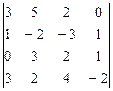 8.
8.  9.
9. 

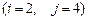



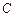 , если
, если 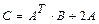 .
.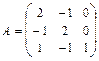 ,
, 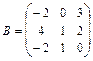 12.
12. 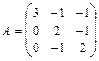 ,
, 
 ,
,  14.
14.  ,
, 
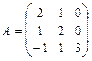 ,
, 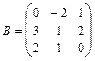 16.
16. 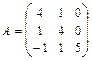 ,
, 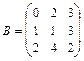
 ,
, 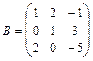 18.
18.  ,
, 
 ,
,  20.
20.  ,
,  .
. .
. 32.
32. 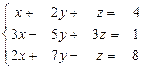
 34.
34. 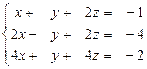
 36.
36. 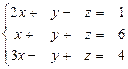
 38.
38. 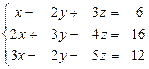
 40.
40. 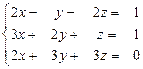
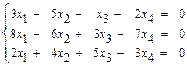 б)
б) 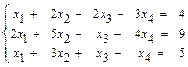
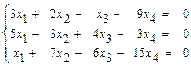 б)
б) 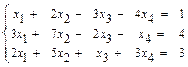
 б)
б) 
 б)
б) 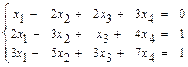
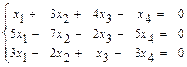 б)
б) 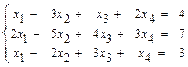
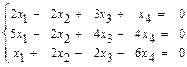 б)
б) 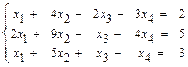
 б)
б) 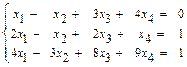
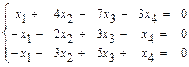 б)
б) 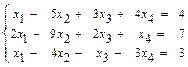
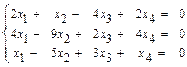 б)
б) 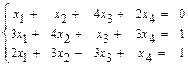
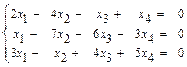 б)
б) 
 .
.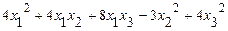 .
. .
. 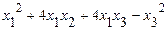 .
. .
.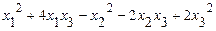 .
.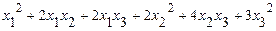 .
.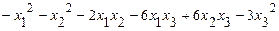 .
. .
. .
.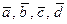 . Требуется:
. Требуется: 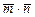 , если
, если  ,
, 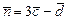 ; б) вычислить векторное произведение векторов
; б) вычислить векторное произведение векторов  ; в) показать, что векторы
; в) показать, что векторы  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.
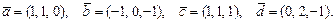
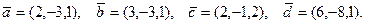

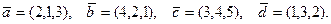

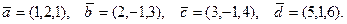


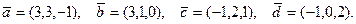
 . Требуется найти:
. Требуется найти: ; б) уравнение стороны
; б) уравнение стороны 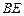 , проведённой из вершины
, проведённой из вершины 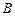 ;
; , проведённой из вершины
, проведённой из вершины 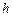 высоты
высоты 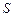 треугольника
треугольника  . 72.
. 72. 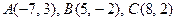
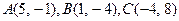 74.
74. 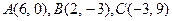
 76.
76. 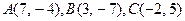
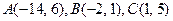 78.
78. 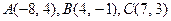
 80.
80. 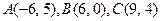
 . Требуется найти:
. Требуется найти: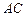 ; б) угол между ребрами
; б) угол между ребрами 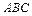 ;
;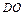 пирамиды
пирамиды  .
.
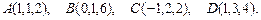
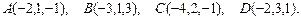
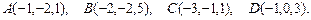
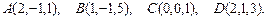
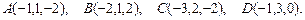
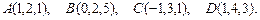
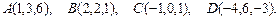
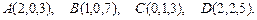
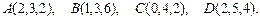
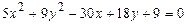 92.
92. 
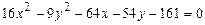 94.
94. 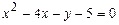
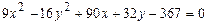 96.
96. 
 98.
98. 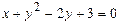
 100.
100. 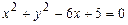
 102.
102. 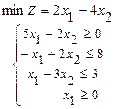 103.
103. 
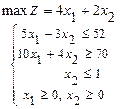 105.
105. 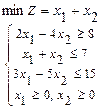 106.
106. 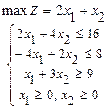
 108.
108. 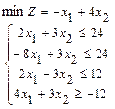
 110.
110. 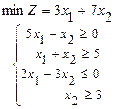
 в следующем периоде (в усл. ден. ед.). Требуется, используя модель Леонтьева многоотраслевой экономики, найти: а) матрицы коэффициентов прямых и полных затрат; б) плановые объёмы выпуска валовой продукции каждой из отраслей, межотраслевые поставки и объёмы выпуска чистой продукции. В ответе записать данные межотраслевого баланса планового периода. (Указание: значения коэффициентов прямых и полных затрат вычислить с точностью до 0.01; значения плановых объёмов выпуска валовой и чистой продукции, межотраслевых поставок округлить до целых значений).
в следующем периоде (в усл. ден. ед.). Требуется, используя модель Леонтьева многоотраслевой экономики, найти: а) матрицы коэффициентов прямых и полных затрат; б) плановые объёмы выпуска валовой продукции каждой из отраслей, межотраслевые поставки и объёмы выпуска чистой продукции. В ответе записать данные межотраслевого баланса планового периода. (Указание: значения коэффициентов прямых и полных затрат вычислить с точностью до 0.01; значения плановых объёмов выпуска валовой и чистой продукции, межотраслевых поставок округлить до целых значений).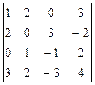
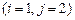
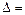
 .
.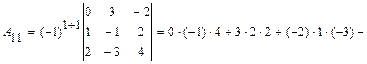
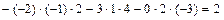
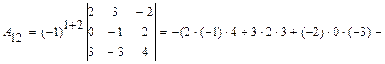
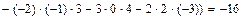

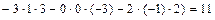
 =
= 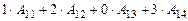 =
= 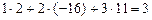
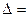
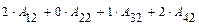 .
.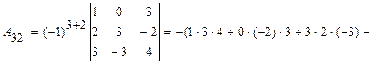
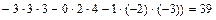
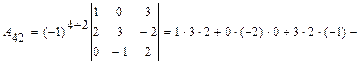
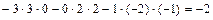
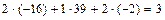 .
. .
. , если:
, если: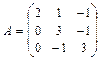 ,
, 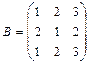 .
. :
: 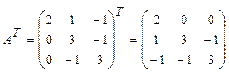 .
.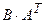 :
: 
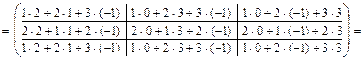
 .
. :
: 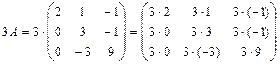
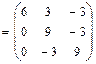 .
.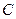 :
: 
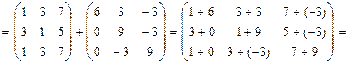
 .
.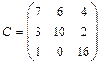 .
.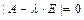 , а множество собственных векторов, отвечающих собственному числу
, а множество собственных векторов, отвечающих собственному числу 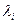 , совпадает с множеством ненулевых решений матричного уравнения:
, совпадает с множеством ненулевых решений матричного уравнения:  , определяемым методом Гаусса.
, определяемым методом Гаусса.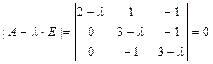 .
.
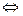
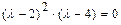
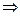
 ,
,  .
. и
и 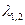 и
и  .
.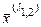 , отвечающих собственному числу
, отвечающих собственному числу 

 ,
,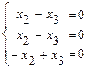 и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе 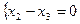 , имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной
, имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной 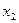 :
:  . Поэтому выбираем в качестве базисной – неизвестную
. Поэтому выбираем в качестве базисной – неизвестную 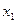 и
и 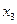 . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения: 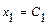 ,
, 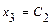 , где
, где 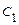 ,
, 
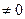 , одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:
, одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов 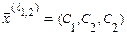 .
.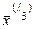 , отвечающих собственному числу
, отвечающих собственному числу 

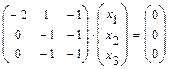 ,
, и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе 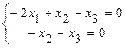 , имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных
, имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные 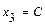 , где
, где 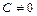 и выражаем через неё значения базисных неизвестных
и выражаем через неё значения базисных неизвестных  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу 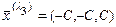 ,
,  . Требуется:
. Требуется:
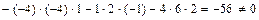 .
. , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: 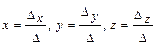
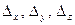 :
: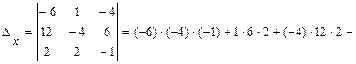
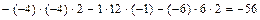 ,
,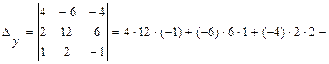
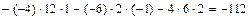 ,
,
 .
. .
.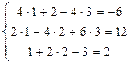
 .
.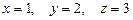 .
.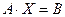 или
или 
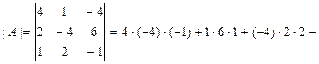
 , то матрица системы
, то матрица системы  и единственное решение системы определяется формулой:
и единственное решение системы определяется формулой:  или
или 
 (методом присоединённой матрицы):
(методом присоединённой матрицы):


