
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений в условиях неопределенностиСодержание книги Поиск на нашем сайте
Обычно теория игр определяется как теория математических моделей выбора оптимальных решений в условиях неопределенности. При этом тип неопределенности, изучаемый в теории игр, характеризуется тем, что рассматриваются ситуации, исход в которых определяется действием нескольких сторон, каждая из которых преследует собственные цели (такие взаимодействия нескольких сторон называются играми). Несовпадение целей действующих сторон, а также определенные ограничения на обмен информацией между ними, приводят к тому, что эти взаимодействия носят конфликтный характер. В данном разделе рассматриваются модели конфликтных ситуаций, которые принято называть играми с природой. Рассматривается некоторая система, которая управляется игроком. Система функционирует тем или иным образом в соответствии с состоянием некоторой среды – природы. Игрок, в соответствии со своими целями, воздействует на систему с помощью альтернативных управляющих воздействий – альтернатив или стратегий. Выбор одной из имеющихся в его распоряжении стратегий называют принятием решения, а игрока – лицом, принимающим решения (ЛПР). Состояние системы определяется двумя факторами: выбранным управляющим воздействием со стороны ЛПР и состоянием среды – природы. Термин "природа" в теории игр понимается в широком смысле. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и т.п. процессы, которые сопровождают экономическую деятельность. Под "природой" может также пониматься рынок, противостоящий предпринимателю, конкурирующая среда, монополия и т.п. "Природа" в виде природных процессов, как часть экономики, не стремиться "специально" навредить предпринимателю. Особенностью данного рода игр является отсутствие конфликта в привычном понимании. Природа неразумна, то есть нейтральна по отношению к игроку и не стремится уменьшить его выигрыш или увеличить свой, она может лишь принимать то или иное состояние. Основная сложность данной задачи, носящая принципиальный характер, связана с отсутствием у игрока информации о состоянии природы. Принципиальным является то обстоятельство, что ЛПР "не знает", в каком состоянии находится среда, то есть не имеет информации о наличном состоянии среды. Именно это обстоятельство имеют в виду, когда говорят, что принятие решения происходит в условиях неопределенности. Однако, эта неопределенность не является абсолютной, так как принимающему решение лицу известно множество состояний среды и известна функция выигрыша – оценка каждого состояния управляемой системы, в зависимости от каждого состояния природы, неким числом, выражающим «полезность» этого состояния для ЛПР. Таким образом, задача принятия решения в условиях неопределенности формулируется следующим образом. Пусть В некоторых случаях значения функции выигрыша имеют характер потерь (затрат), то есть, фактически они являются не выигрышами, а проигрышами. Рассматривается матрица Очевидно, ЛПР при выборе той или иной стратегии рискует. В ситуации неопределенности нужно принимать решения, руководствуясь какими либо соображениями предварительного характера. Если матрица результатов представлена матрицей выигрышей (доходов) Если матрица результатов представлена матрицей проигрышей (затрат) Требуется указать наилучшую в некотором смысле альтернативу, или, найти оптимальную стратегию. ЛПР должно руководствоваться какими-то соображениями при выборе стратегий, сравнивая их по «эффективности» между собой. Самый естественный принцип сравнения альтернатив это принцип доминирования, который применяется также при решении матричных и биматричных игр, который формулируется следующим образом. Стратегия Очевидно, что если Для того чтобы выбрать из оставшихся стратегий оптимальную, нужны какие-то дополнительные соображения. Основной метод, позволяющий ЛПР найти оптимальную стратегию в условиях неопределенности, состоит в том, что формулируется некоторая гипотеза о поведении среды, позволяющая дать численную оценку каждой стратегии. Оптимальной считается та стратегия, для которой численная оценка является максимальной. Задание оценки каждой стратегии позволяет сравнить любые две стратегии: из двух стратегий лучшей считается та, которая имеет большую оценку (стратегии, имеющие одинаковую численную оценку, считаются эквивалентными). Таким образом, устанавливаются критерии для сравнения стратегий. Среди критериев выделяют классические и производные (составные). К классическим критериям, применяемым для решения игр в условиях неопределенности, относят критерии Лапласа, Вальда, Севиджа.
Критерий Лапласа. (Принцип недостаточного основания). Игрок не имеет никакой информации о вероятности, с которой природа может принять то или иное состояние. ЛПР принимает гипотезу: все состояния Если матрица результатов представлена матрицей выигрышей (доходов) Оптимальная по данному критерию стратегия
Замечание. Если матрица результатов представлена матрицей проигрышей (затрат)
Критерий Вальда. (Принцип крайнего пессимизма). Данный критерий, в зависимости от вида функции выигрышей, имеет форму принципа максимина или принципа минимакса. ЛПР принимает гипотезу: при выборе той или иной стратегии надо рассчитывать на худший из возможных вариантов. Принцип максимина. Функцией выигрыша является матрица выигрышей Принцип минимакса. Функцией выигрыша является матрица проигрышей В качестве оценки стратегии Оптимальная по данному критерию стратегия Критерий Севиджа. (Принцип минимального риска). ЛПР анализирует матрицу рисков и принимает гипотезу о том, что складывается ситуация максимального риска (следует избегать большого риска при принятии решений). В качестве оценки стратегии Этот критерий является мерой сожаления о незнании истинного состояния среды и рекомендует выбрать ту стратегию, которая в самой неблагоприятной ситуации сводит риск к минимуму.
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.132.43 (0.007 с.) |

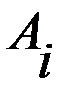 (i = 1, 2, 3, …, m) – множество стратегий игрока,
(i = 1, 2, 3, …, m) – множество стратегий игрока, 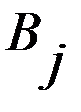 (j = 1, 2, 3, …, n) – множество состояний природы, совокупность чисел
(j = 1, 2, 3, …, n) – множество состояний природы, совокупность чисел 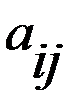 – функция выигрыша игрока, то есть оценка полезности (с точки зрения ЛПР) того состояния системы, которое возникает, если игрок выбирает управляющее воздействие
– функция выигрыша игрока, то есть оценка полезности (с точки зрения ЛПР) того состояния системы, которое возникает, если игрок выбирает управляющее воздействие 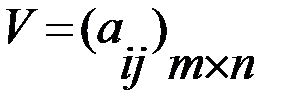 , которая аналогична виду платежной матрицы P в матричных играх, при этом
, которая аналогична виду платежной матрицы P в матричных играх, при этом 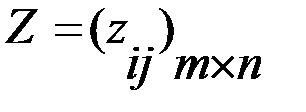 – «функция проигрыша», при этом
– «функция проигрыша», при этом 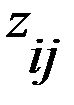 есть значение проигрыша (затрат) в ситуации, когда игрок выбирает i – ую стратегию, а среда принимает j – ое состояние.
есть значение проигрыша (затрат) в ситуации, когда игрок выбирает i – ую стратегию, а среда принимает j – ое состояние.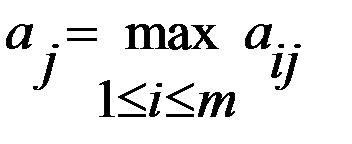 при каждом состоянии природы
при каждом состоянии природы 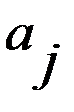 – наибольшее число в каждом j –ом столбце). Затем составляется матрица рисков
– наибольшее число в каждом j –ом столбце). Затем составляется матрица рисков  , где каждая компонента
, где каждая компонента  представляет собой риск в каждой ситуации, то есть недополученный, по сравнению с самым высоким при данном состоянии природы, доход.
представляет собой риск в каждой ситуации, то есть недополученный, по сравнению с самым высоким при данном состоянии природы, доход. 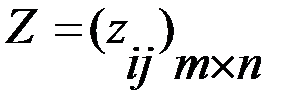 , то ЛПР выбирает минимальный проигрыш
, то ЛПР выбирает минимальный проигрыш  . Затем составляется матрица рисков
. Затем составляется матрица рисков 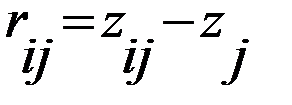 .
. (
(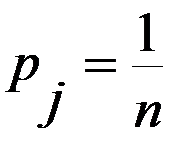 ).
). .
. 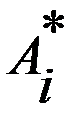 находится из условия:
находится из условия: 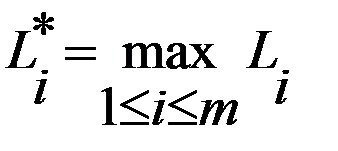 .
.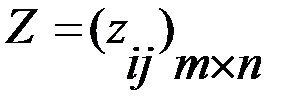 , то в качестве оценки стратегии
, то в качестве оценки стратегии 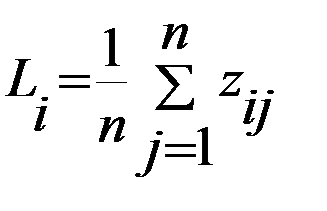 . Оптимальная по данному критерию стратегия
. Оптимальная по данному критерию стратегия 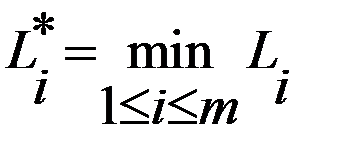 .
.
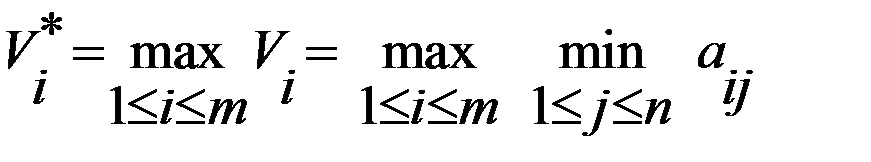 .
. 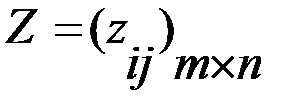 , где
, где 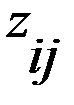 есть значения функции проигрыша в ситуации, когда игрок выбирает i – ую стратегию, а среда принимает j – ое состояние.
есть значения функции проигрыша в ситуации, когда игрок выбирает i – ую стратегию, а среда принимает j – ое состояние. .
. .
. 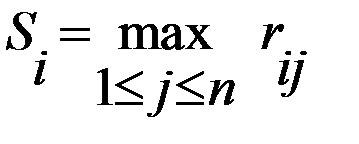 .Оптимальная по данному критерию стратегия
.Оптимальная по данному критерию стратегия  .
.


