
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Р авновесие по Нэшу в смешанных стратегиях.Содержание книги Поиск на нашем сайте
Во всех рассмотренных выше примерах имелись в наличии равновесия по Нэшу, которые определялись либо путем последовательного удаления строго доминирующих стратегий обоими игроками, либо же, при отсутствии таковых, путем графического анализа доминирования. Однако зачастую возникают ситуации, когда у игроков отсутствуют доминирующие стратегии и устойчивые равновесия в чистых стратегиях.
Пример 1.Отсутствие равновесия в чистых стратегиях Т а б л и ц а 2.9 Т а б л и ц а 2.10 Матрица А Матрица В
У игроков отсутствуют доминирующие стратегии и в результате графического анализа доминирования приходим к случаю, когда в соответствующих клетках платежных матриц отсутствуют одновременно выделенные элементы (см. та б л. 2.9 и та б л. 2.10), что иллюстрирует отсутствие равновесия по Нэшу в чистых стратегиях. Здесь рассматриваются биматричные одноходовые игры размерности Возможность многократного повторения игры позволяет перейти к поиску её решения в смешанных стратегиях. Смешанные стратегии игроков в биматричных играх определяются точно также как в антагонистических матричных играх. Теорема Нэймана. Если биматричная игра не имеет решения (оптимума) в чистых стратегиях, то она имеет по крайней мере одно равновесие в смешанных стратегиях.
Перейдём к поиску решения игры в смешанных стратегиях. Смешанные стратегии первого игрока
Смешанные стратегии второго игрока
Если какая либо стратегия выбирается игроком с вероятностью равной единице, то матрицы выбора смешанных стратегий вырождаются в матрицы выбора чистых стратегий. По аналогии с формированием результатов при использовании чистых стратегий запишем результаты, которые может получить каждый из игроков, выбирая определённую смесь своих стратегий, но при условии, что противник выбрал конкретную чистую стратегию. Выигрыш первого игрока при заданных смешанных стратегиях Выигрыш первого игрока при заданных смешанных стратегиях При выборе смешанных стратегий
В то же время первый игрок, выбирая в заданной смеси свои собственные стратегии
где значение Аналогично определяются выигрыши второго игрока при его заданных смешанных стратегиях или При условии выбора первым игроком чистых стратегий, второй игрок, выбирая смешанные стратегии
В то же время второй игрок, выбирая в заданной смеси свои собственные стратегии
где значение Найдём средние выигрыши обоих игроков при использовании ими смешанных стратегий
и второго
Задача выбора оптимальных смешанных стратегий, обеспечивающих максимизацию выигрышей каждого из игроков представляется в виде совокупности условий и ограничений, которая формулируется как задача линейного программирования:
Решением такой задачи является пара смешанных стратегий
Определение. Пара смешанных стратегий
при условии, что 2.5. Аналитический метод решения биматричной игры 2
При высоких размерностях платежных матриц ( (2 Воспользуемся полученными в п. 3.1.4. выражениями для средних выигрышей первого и второго игроков, при смешанных стратегиях
Здесь
и второго игроков
Откуда находим
и
Продифференцируем полученные выражения
Координаты
Замечание 1. Равенство нулю первой производной даёт условие критической точки, которая отражает необходимое, но вовсе не достаточное условие экстремума, которым может быть как минимум, так и максимум. В данной задаче не требуется дополнительных исследований достаточности и именно максимума, всё это гарантирует теорема Дж. Нэймана. Решая полученные уравнения, найдем выражения для оптимальной по Нэшу смеси стратегий в биматричной игре
Замечание 2. Из полученных формул видно, что хотя бы одна из величин Необходимо отметить, что средние выигрыши обоих игроков при использовании оптимальной смеси стратегий превышают для каждого из них два своих наихудших результата в чистых стратегиях. В то же время оба средних выигрыша уступают для каждого игрока двум лучшим результатам в чистых стратегиях.
2.6. Графический метод решения биматричной игры 2
В случае минимальных размерностей платежных матриц поиск решения в смешанных стратегиях можно проиллюстрировать графически. Сформулированные в п. 3.1.4, определяющие ситуацию равновесия, условия выглядят следующим образом
Таким образом, равновесная ситуация определяется парой смешанных стратегий
которая приводится к виду
Дальнейшее решение ищем, при совокупности ограничений
Приемлемые решения для второго игрока находятся как решение системы неравенств
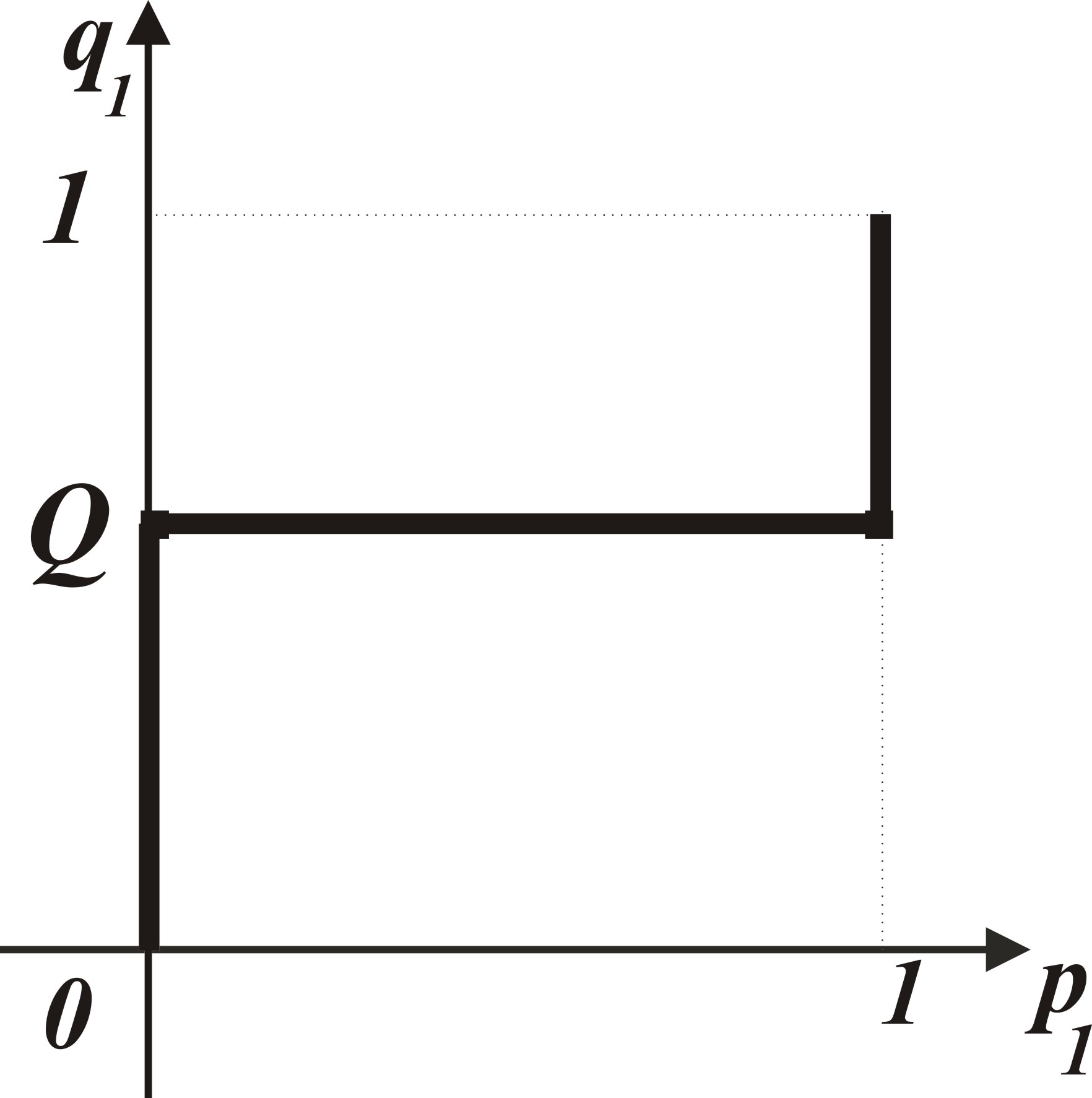
Рассмотрим следующие три ситуации. 1)
Разделив на выражение Случай 1.1 (см. рис. 3.1). Случай 1.2 (см. рис. 3.2).
Рис. 2.1 Рис. 2.2
2)
Разделив обе части второго неравенства на выражение Случай 2.1 (см. рис. 3.3). Случай 2.2 (см. рис. 3.4).
Рис. 2.3 Рис. 2.4
3) В случае
Поскольку системе в последнем случае получаем систему
Рис.2.5 Объединяя три случая, а именно представленное на рис. 3.6 или представленное на рис. 3.7, при выполнении условия при выполнении условия
Рис. 2.6 Рис. 2.7
Переходим к поиску решений для первого игрока, которые находятся как решение следующей системы
Рассмотрим следующие три ситуации. 4)
Разделив обе части первого неравенства на выражение Случай 4.1 (см. рис. 3.8). Случай 4.2 (см. рис. 3.9).
Рис. 2.8 Рис. 2.9
5)
Разделив обе части второго неравенства на выражение Случай 5.1 (см. рис. 3.10). Случай 5.2 (см. рис. 3.11).
Рис. 2.10 Рис. 2.11
6) В случае
Cистеме В случае
Рис. 2.12 Объединяя три случая, а именно представленное на рис. 3.13 или представленное на рис. 3.14, при выполнении условия при выполнении условия
Рис. 2.13 Рис. 2.14
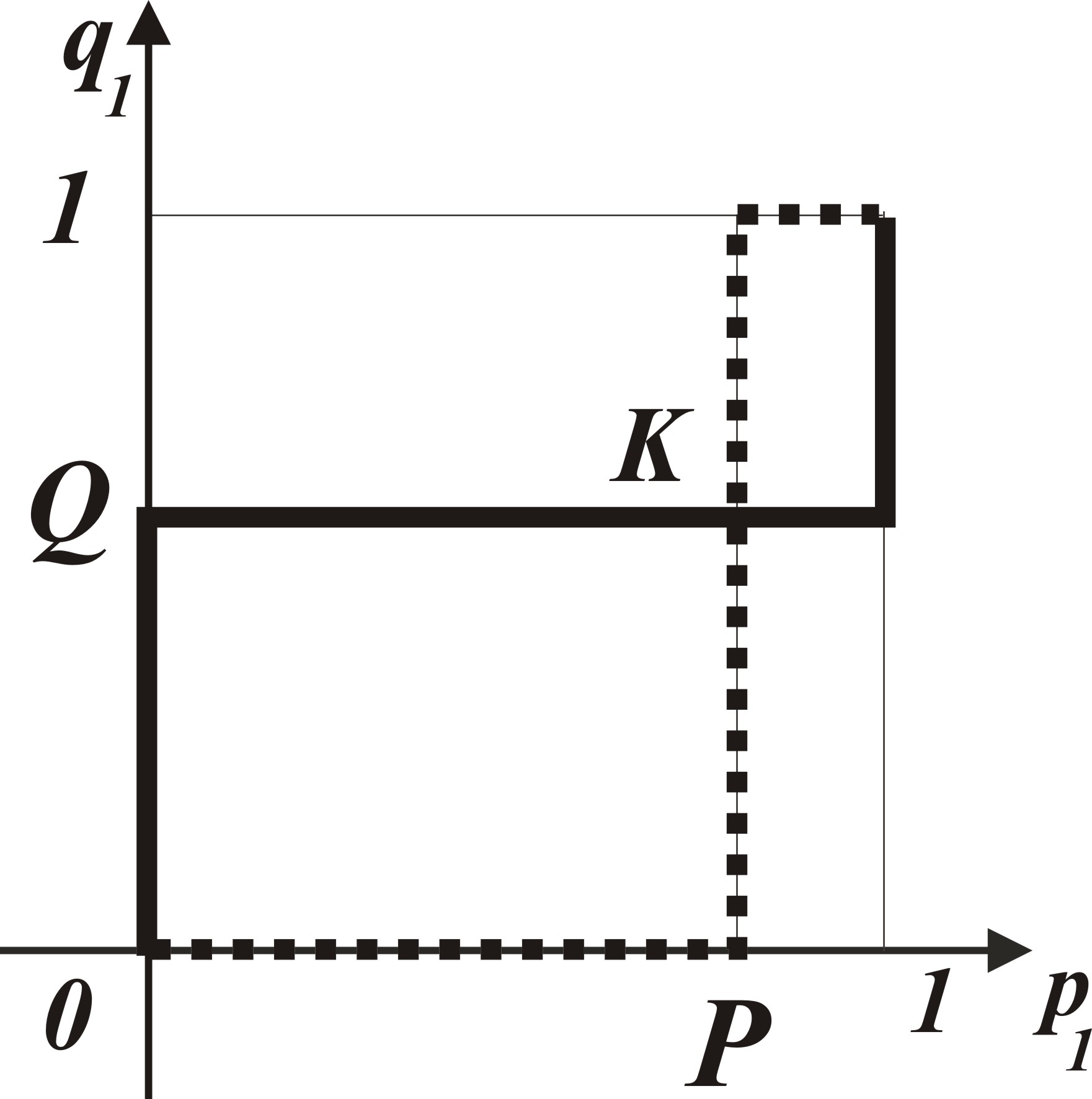
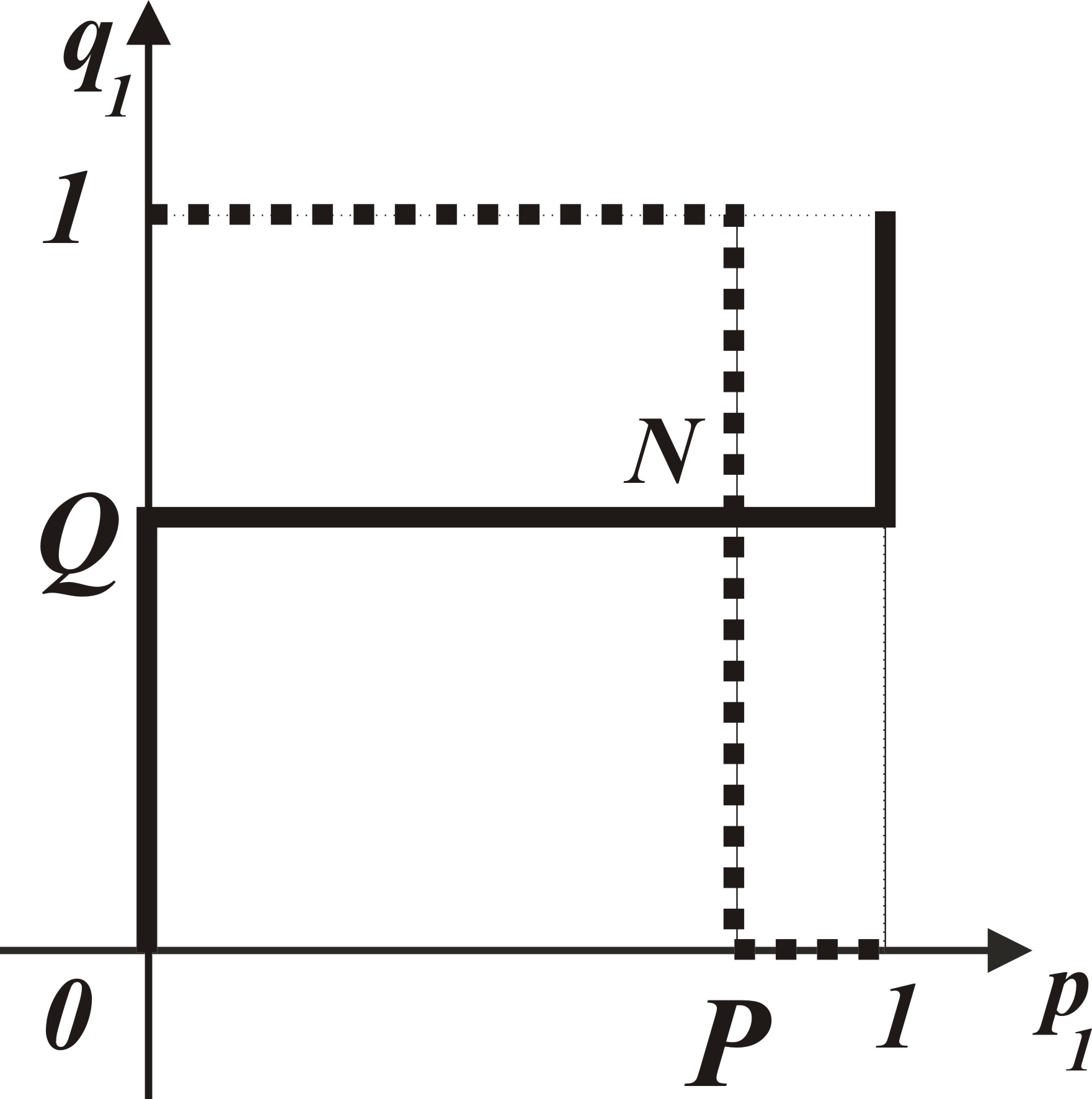
Совокупность оптимальных решений обоих игроков определяется графически, как координаты общих точек, полученных при наложении графиков и здесь возможны четыре случая. В первом случае (см. рис. 3.15), Во втором случае (см. рис. 3.16), при выполнении условий при выполнении условий налагая графики, изображенные налагая графики, изображенные на рисунках рис. 3.6 и рис. 3.13, на рисунках рис. 3.6 и рис. 3.14, находим точку К с координатами находим точку L с координатами
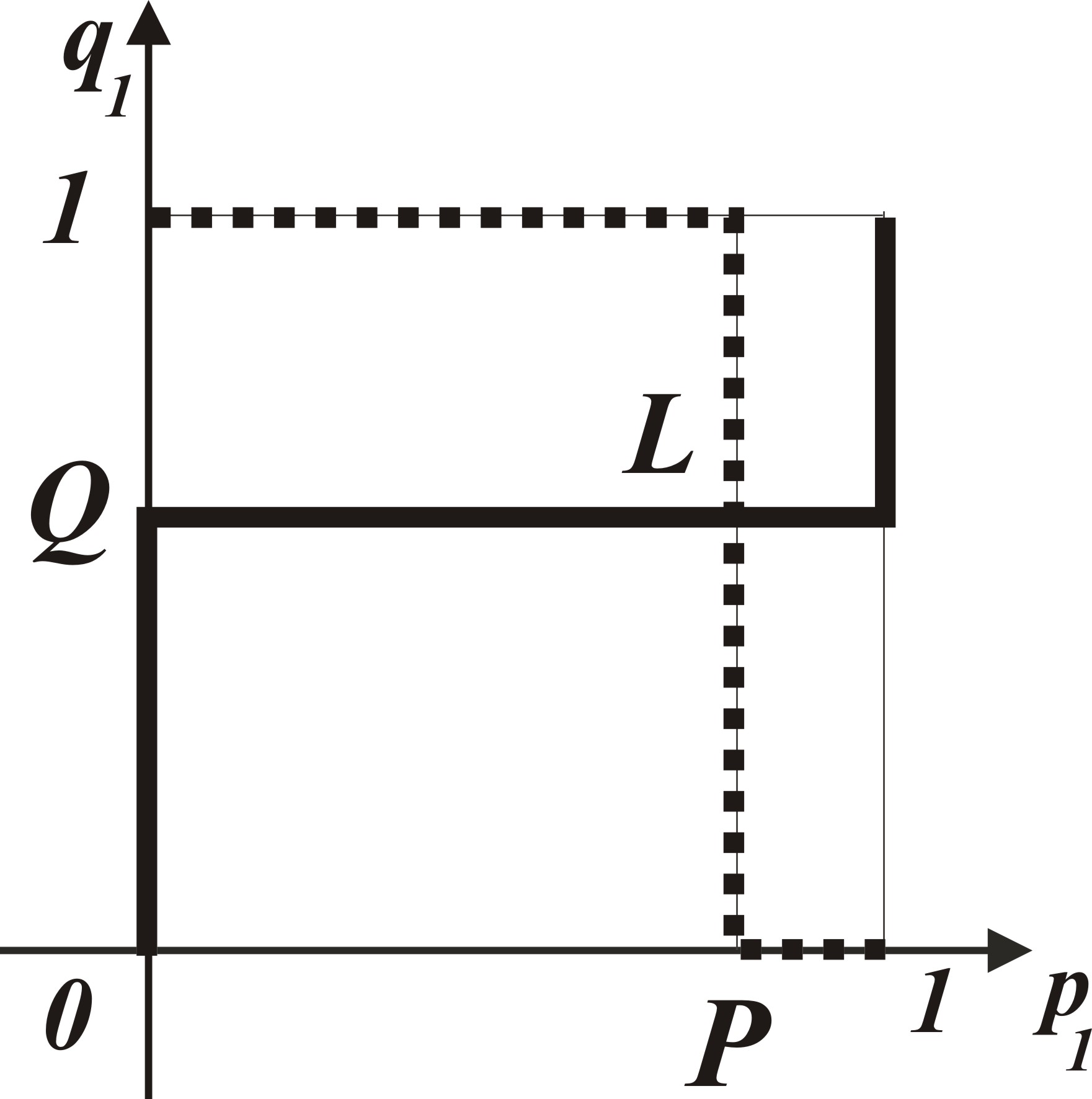
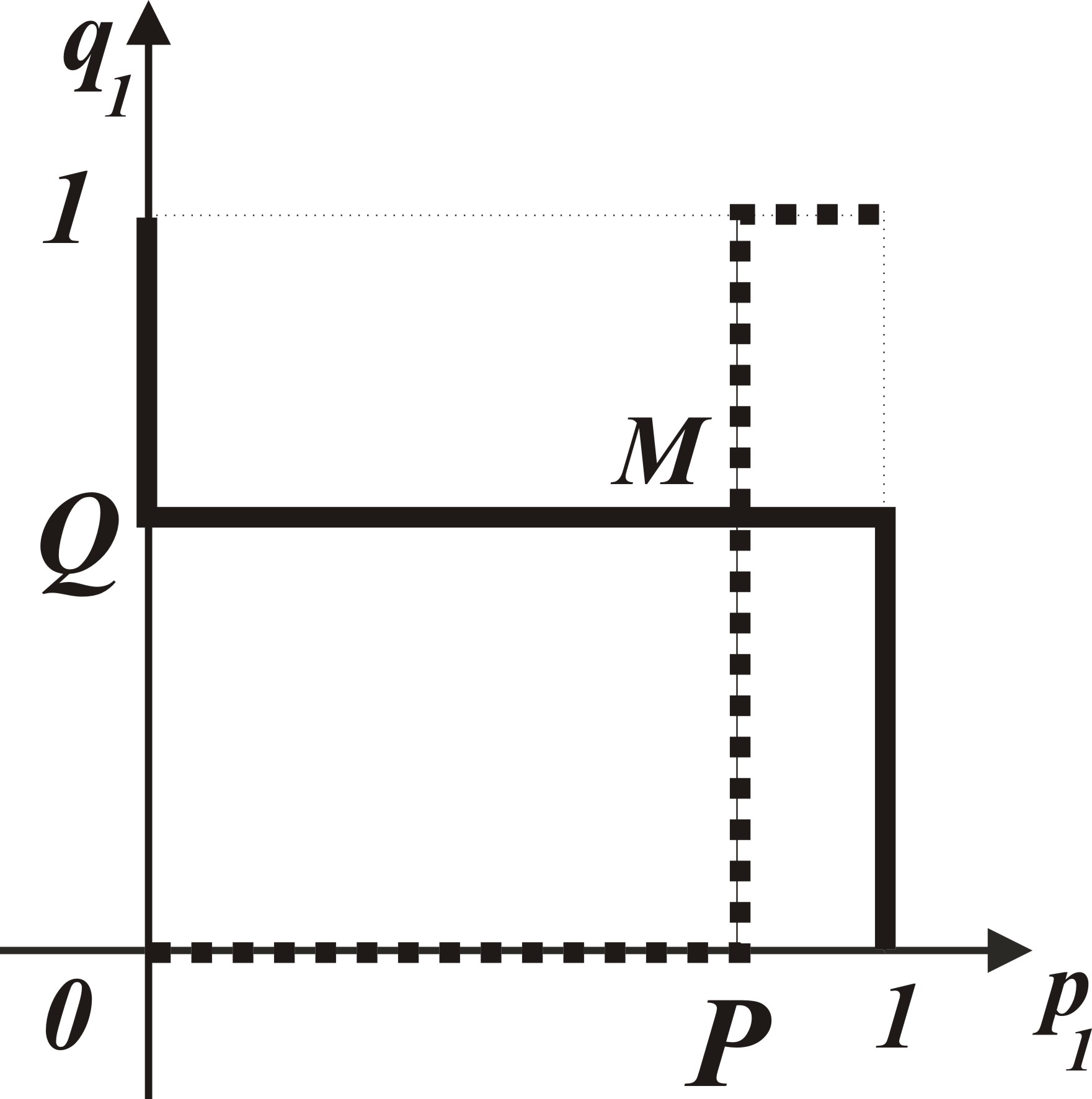
Рис. 2.15 Рис. 2.16 В первом случае (рис. 3.15) общими точками являются также точка с координатами (0; 0) и точка с координатами (1; 1). В третьем случае (см. рис. 3.17), В четвертом случае (см. рис. 3.18), при выполнении условий при выполнении условий налагая графики, изображенные налагая графики, изображенные на рисунках рис. 3.7 и рис. 3.13, на рисунках рис. 3.6 и рис. 3.14, находим точку М с координатами находим точку N с координатами
Рис. 2.17 Рис. 2.18 С учетом выражений
Соответственно, средние выигрыши игроков находятся по формулам
ИГРЫ С ПРИРОДОЙ
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.98 (0.014 с.) |

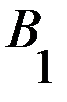

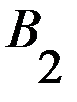

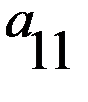
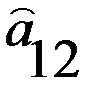
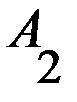

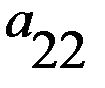
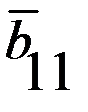

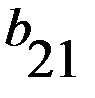

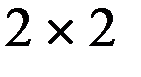 , в которых игроки делают ходы одновременно. Такие игры могут повторяться много раз, но в рассматриваемой постановке считается, что какой бы раз не повторялась данная игра, платёжная матрица остаётся неизменной и поэтому не изменяются оптимальные решения, то есть время не влияет на поведение игроков и на выбор оптимальных стратегий (именно поэтому такие игры еще называются статическими).
, в которых игроки делают ходы одновременно. Такие игры могут повторяться много раз, но в рассматриваемой постановке считается, что какой бы раз не повторялась данная игра, платёжная матрица остаётся неизменной и поэтому не изменяются оптимальные решения, то есть время не влияет на поведение игроков и на выбор оптимальных стратегий (именно поэтому такие игры еще называются статическими).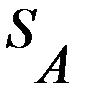 =
=  , где
, где 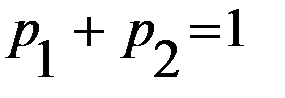 ,
, 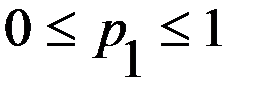 ,
, 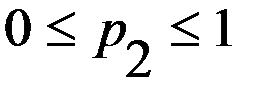 .
. =
=  , где
, где 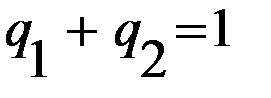 ,
, 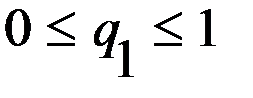 ,
, 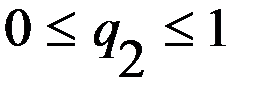 .
.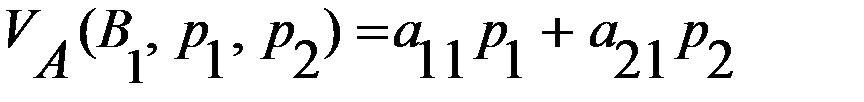 .
. , составит
, составит  .
.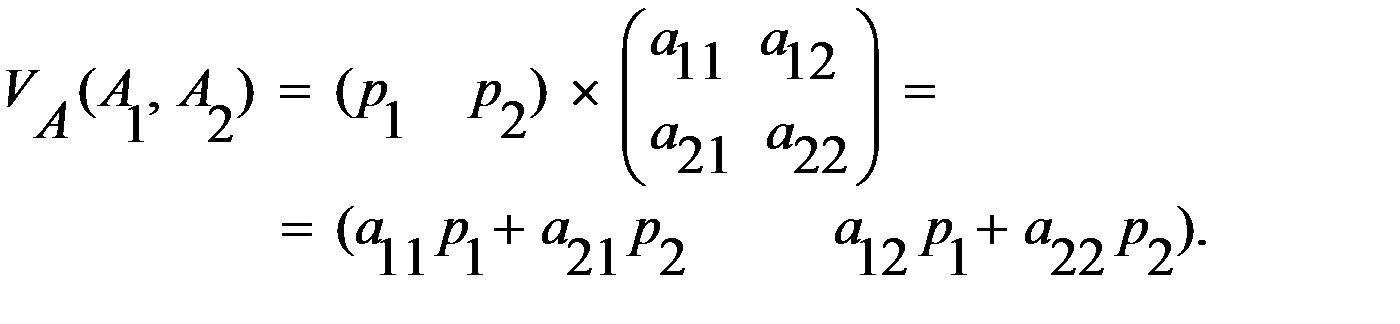
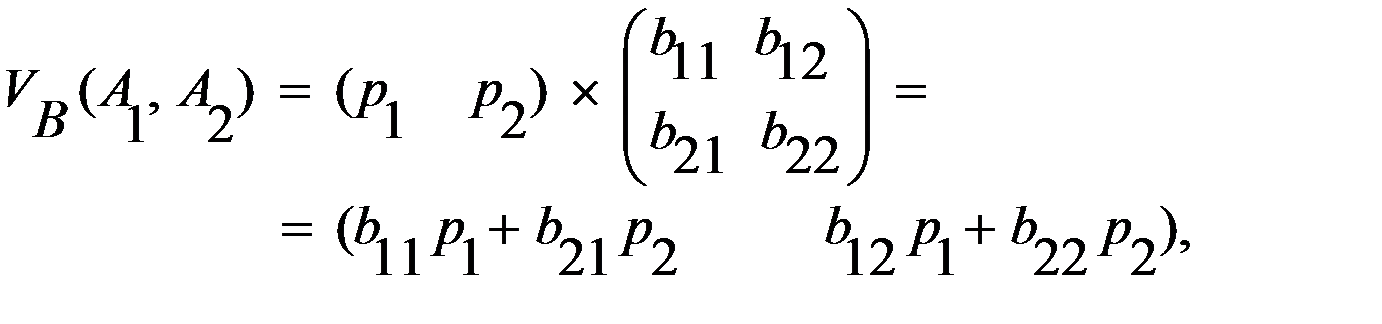
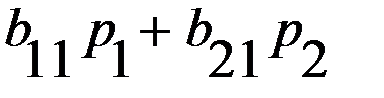 – выигрыш второго игрока, при условии, что он выбрал первую стратегию, а значение
– выигрыш второго игрока, при условии, что он выбрал первую стратегию, а значение  – выигрыш второго игрока, при условии, что он выбрал вторую стратегию.
– выигрыш второго игрока, при условии, что он выбрал вторую стратегию.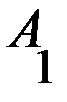 – первую стратегию
– первую стратегию 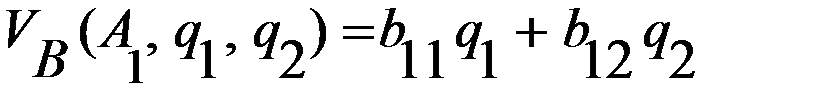 ,
,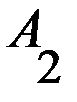 – вторую стратегию
– вторую стратегию 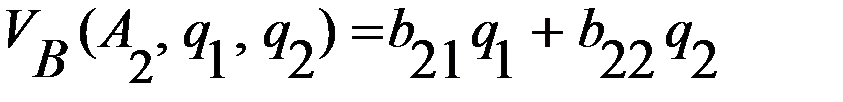 .
.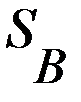 , получает результат
, получает результат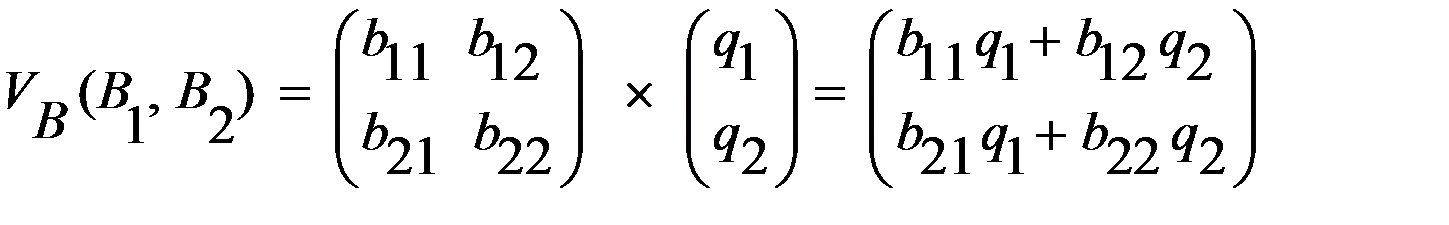 .
. , пытается оценить результаты первого игрока при условии, что тот придерживается одной из своих чистых стратегий
, пытается оценить результаты первого игрока при условии, что тот придерживается одной из своих чистых стратегий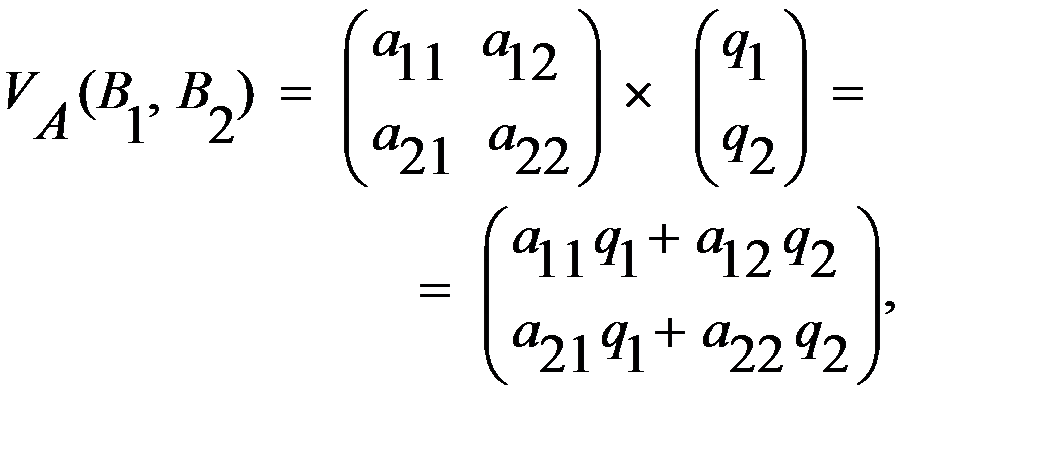
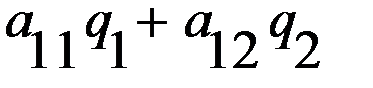 – выигрыш первого игрока, при условии, что он выбрал первую стратегию, а значение
– выигрыш первого игрока, при условии, что он выбрал первую стратегию, а значение 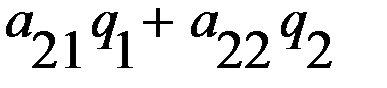 – выигрыш первого игрока, при условии, что он выбрал вторую стратегию.
– выигрыш первого игрока, при условии, что он выбрал вторую стратегию.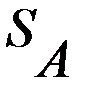 и
и 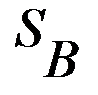 , первого
, первого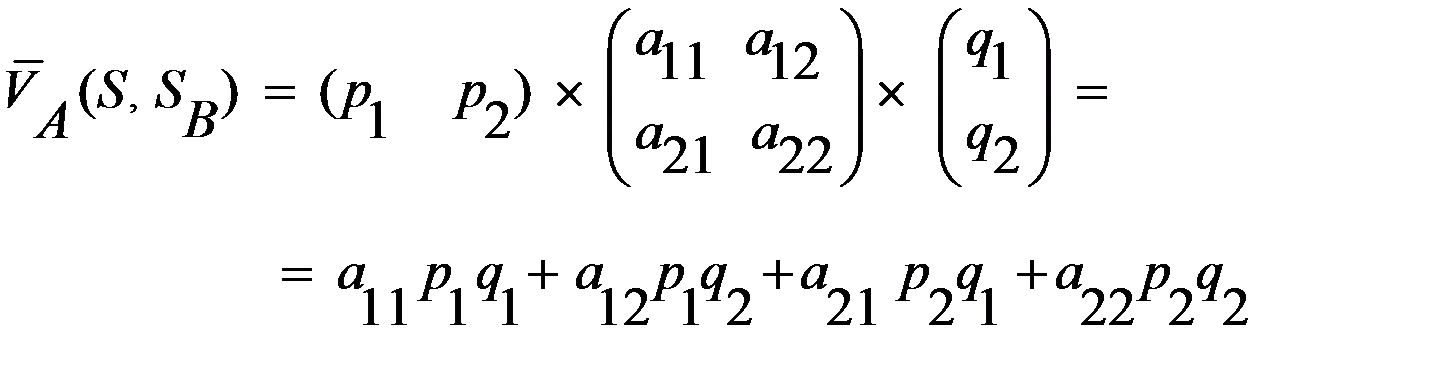
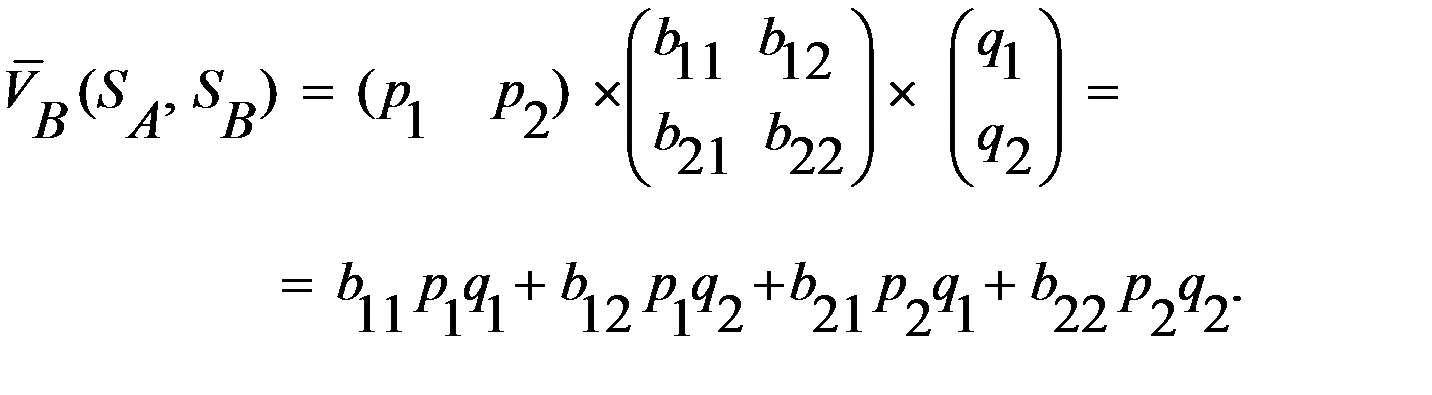
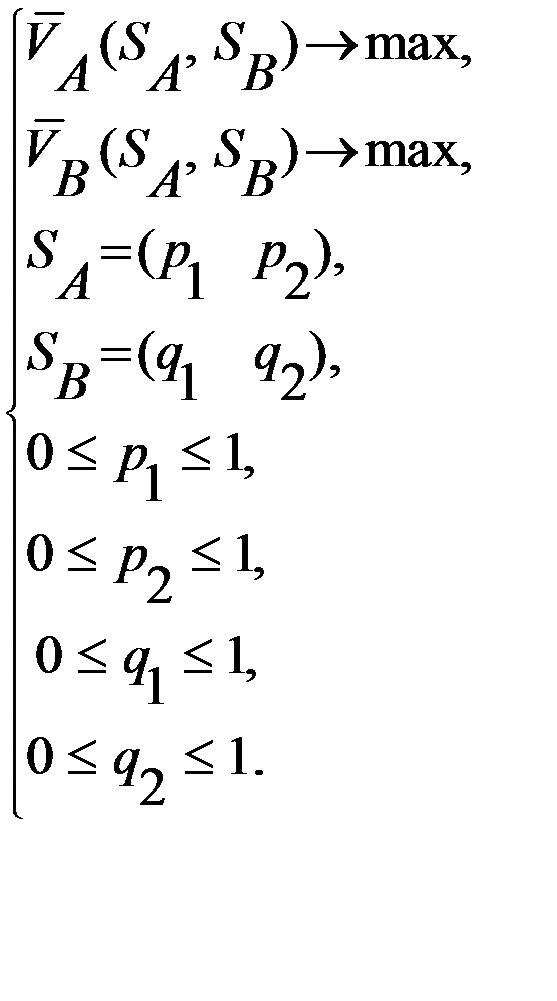
 и
и  , обеспечивающая получение игроками максимальных средних выигрышей
, обеспечивающая получение игроками максимальных средних выигрышей  и
и 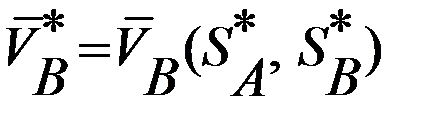 .
.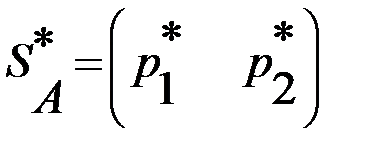 и
и  игроков называется равновесием по Нэшу в смешанных стратегиях, если ни одному из игроков невыгодно отклоняться от этих стратегий в одиночку, т.е. когда для любых
игроков называется равновесием по Нэшу в смешанных стратегиях, если ни одному из игроков невыгодно отклоняться от этих стратегий в одиночку, т.е. когда для любых  и
и 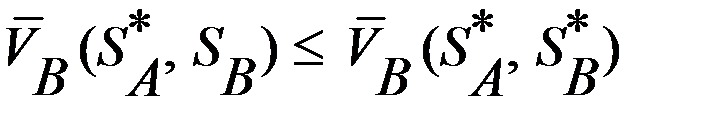 ,
,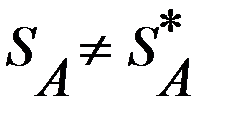 и
и 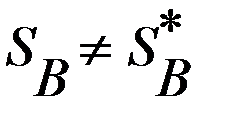 .
. 2
2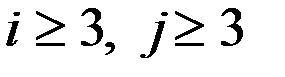 ) оптимальное решение находят численными методами. При минимальной
) оптимальное решение находят численными методами. При минимальной и
и  ,
,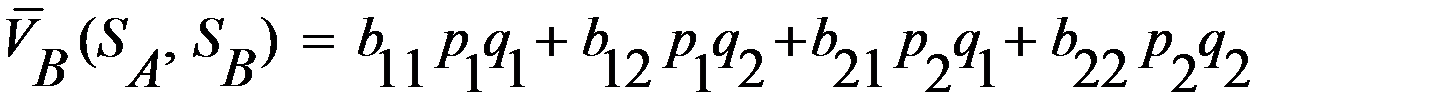 .
.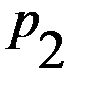 и
и  через первые координаты, а именно как
через первые координаты, а именно как 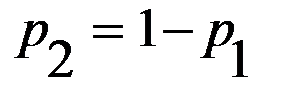 и
и  , получим выражения средних выигрышей первого
, получим выражения средних выигрышей первого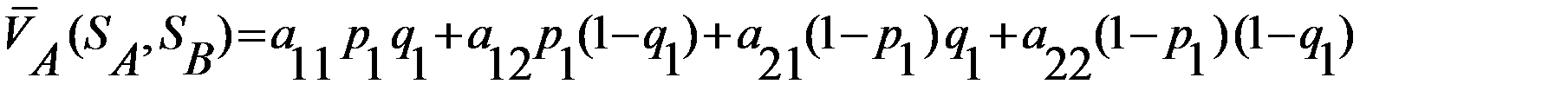
 .
.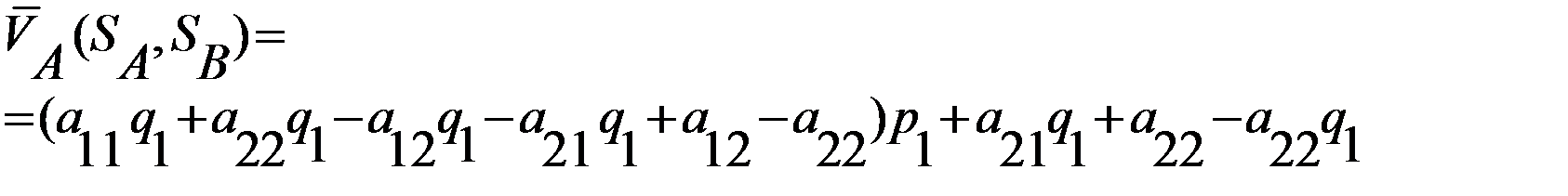
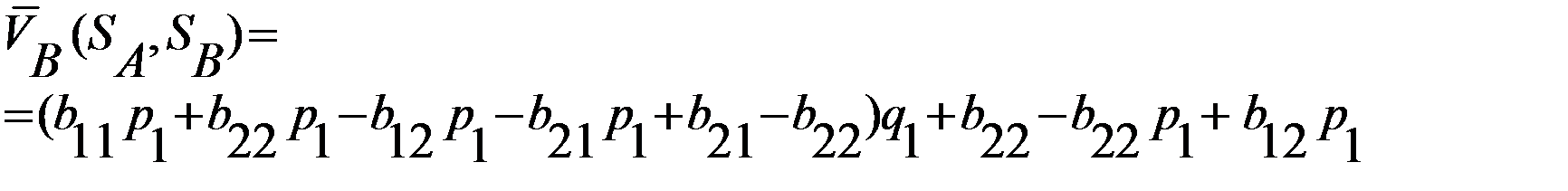 .
.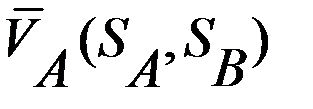 и
и 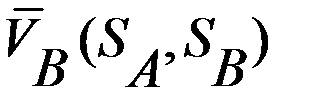 по переменным
по переменным  и
и 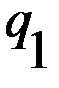 , соответственно,
, соответственно,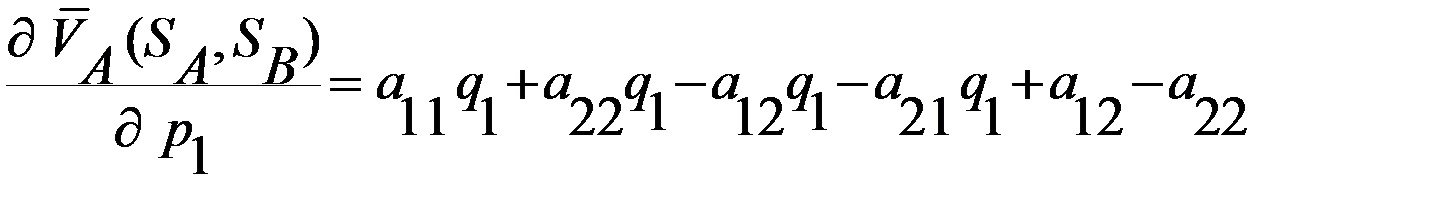 ,
,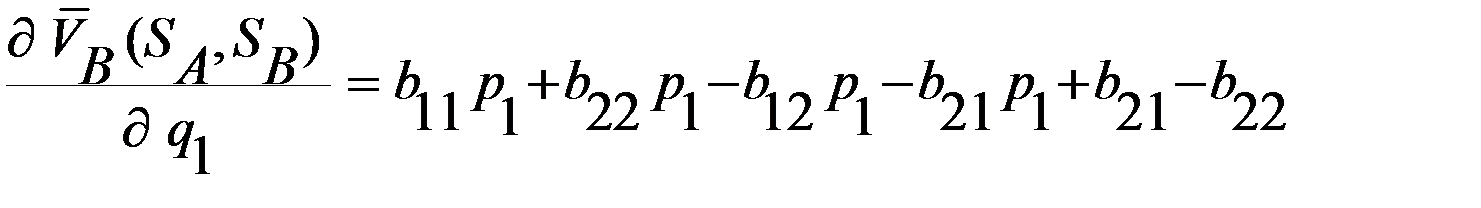 .
. и
и 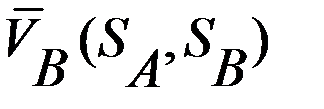 найдем, приравняв нулю частные производные
найдем, приравняв нулю частные производные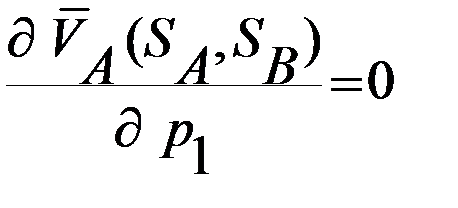

 ,
,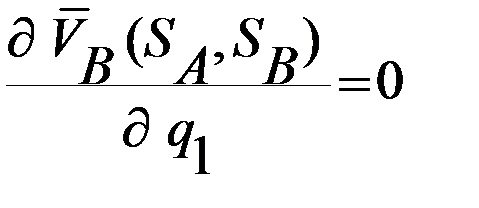
 .
.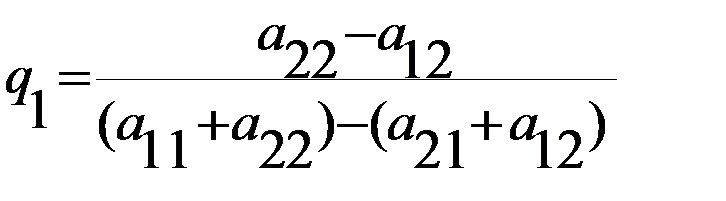 ,
, 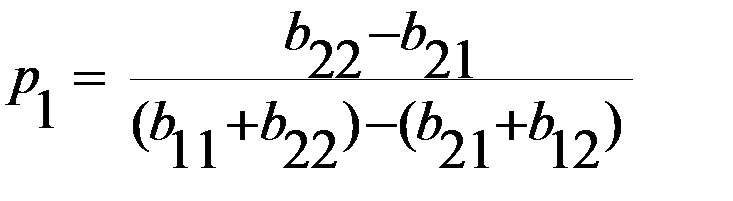 ,
, 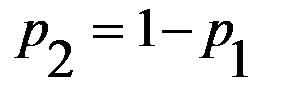 .
.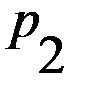 ,
, 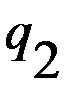 может оказаться отрицательной. Это означает, что существует решение в чистых стратегиях.
может оказаться отрицательной. Это означает, что существует решение в чистых стратегиях.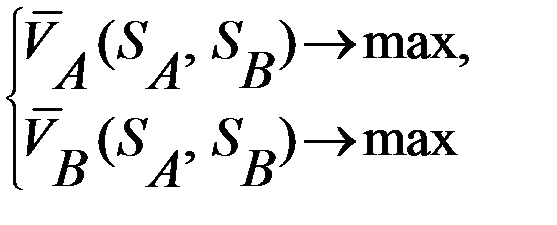 или
или 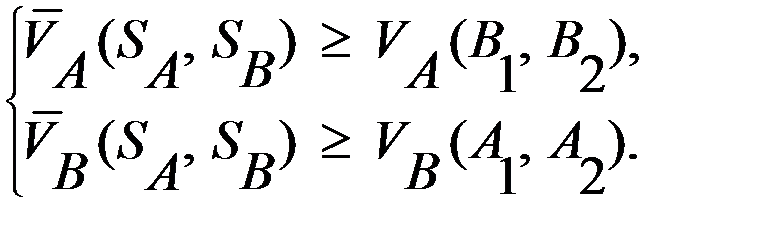
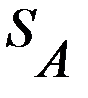 ,
,  , удовлетворяющих системе неравенств
, удовлетворяющих системе неравенств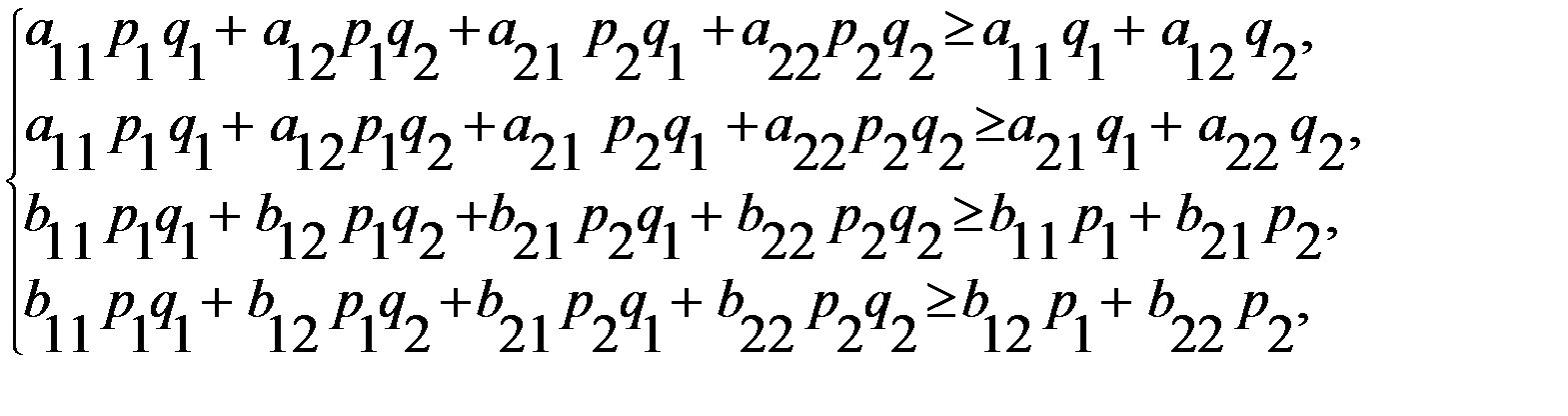
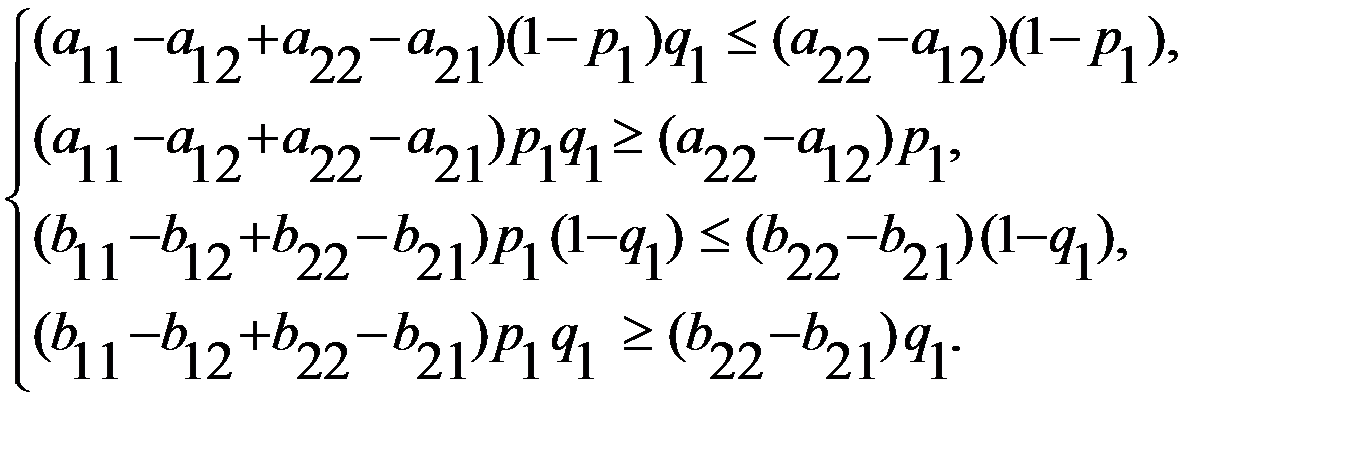

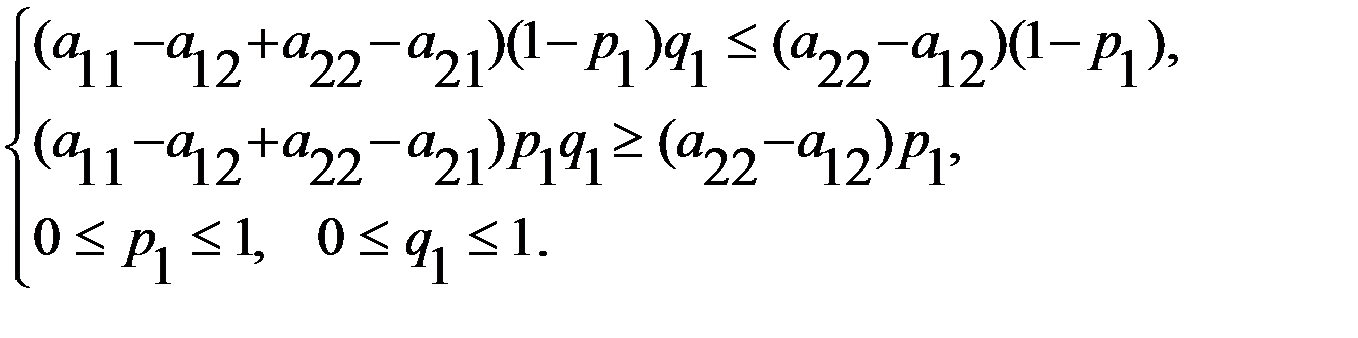
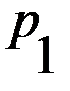 = 0 и система принимает вид
= 0 и система принимает вид
 , обе части первого неравенства, с учетом обозначения
, обе части первого неравенства, с учетом обозначения 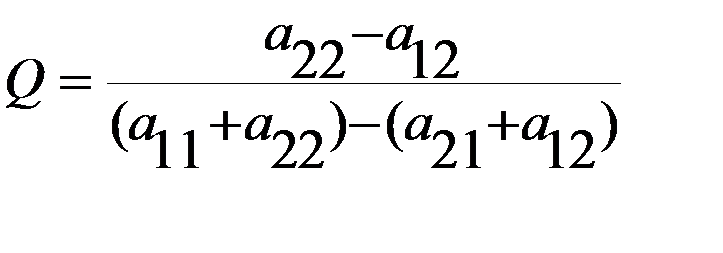 , полу-чим два случая (в зависимости от знака делителя).
, полу-чим два случая (в зависимости от знака делителя).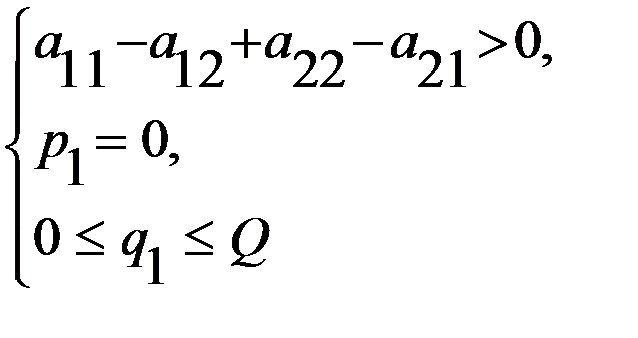 или
или 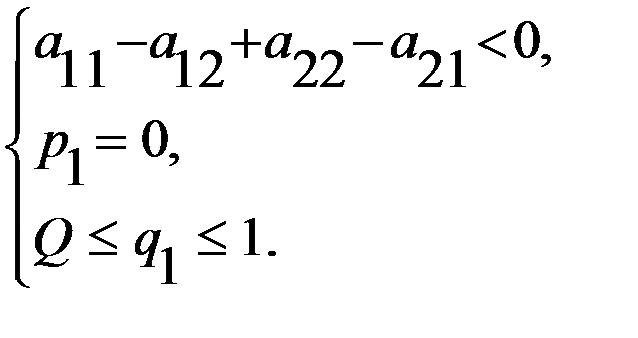
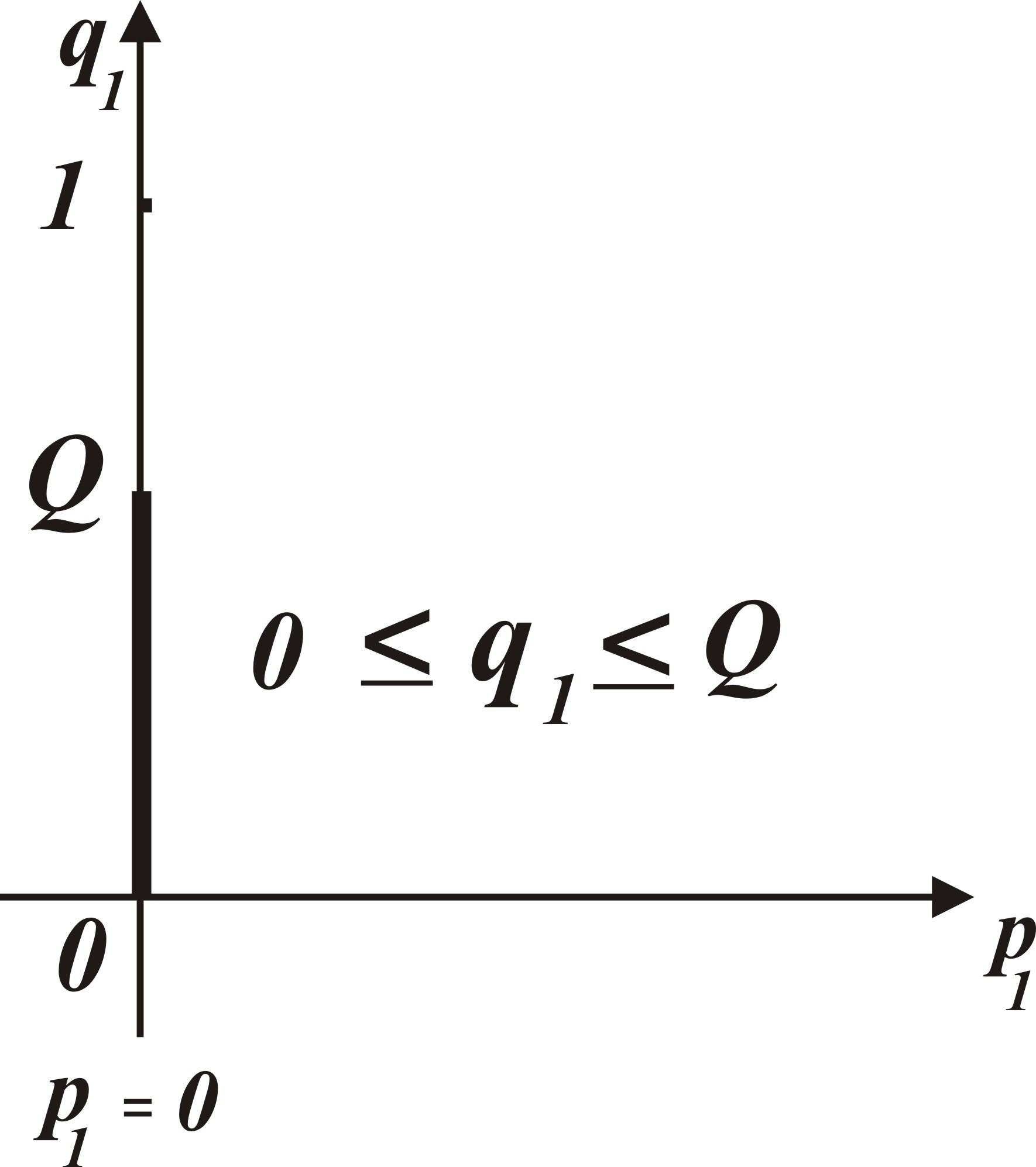

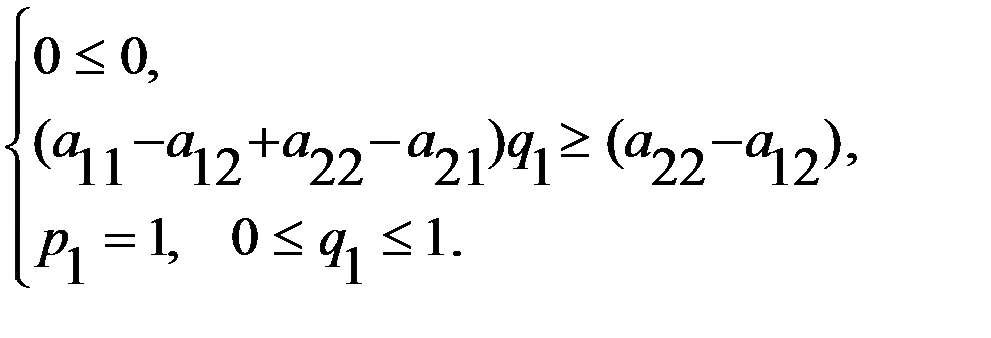
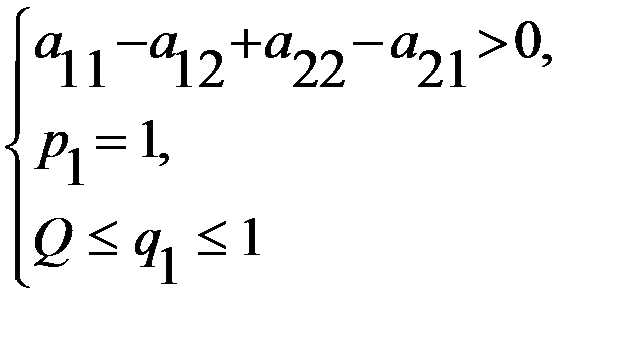 или
или 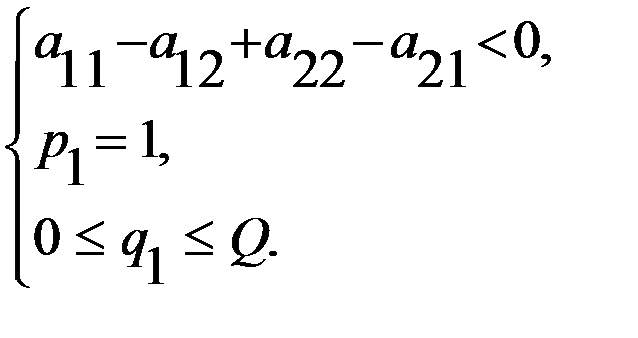

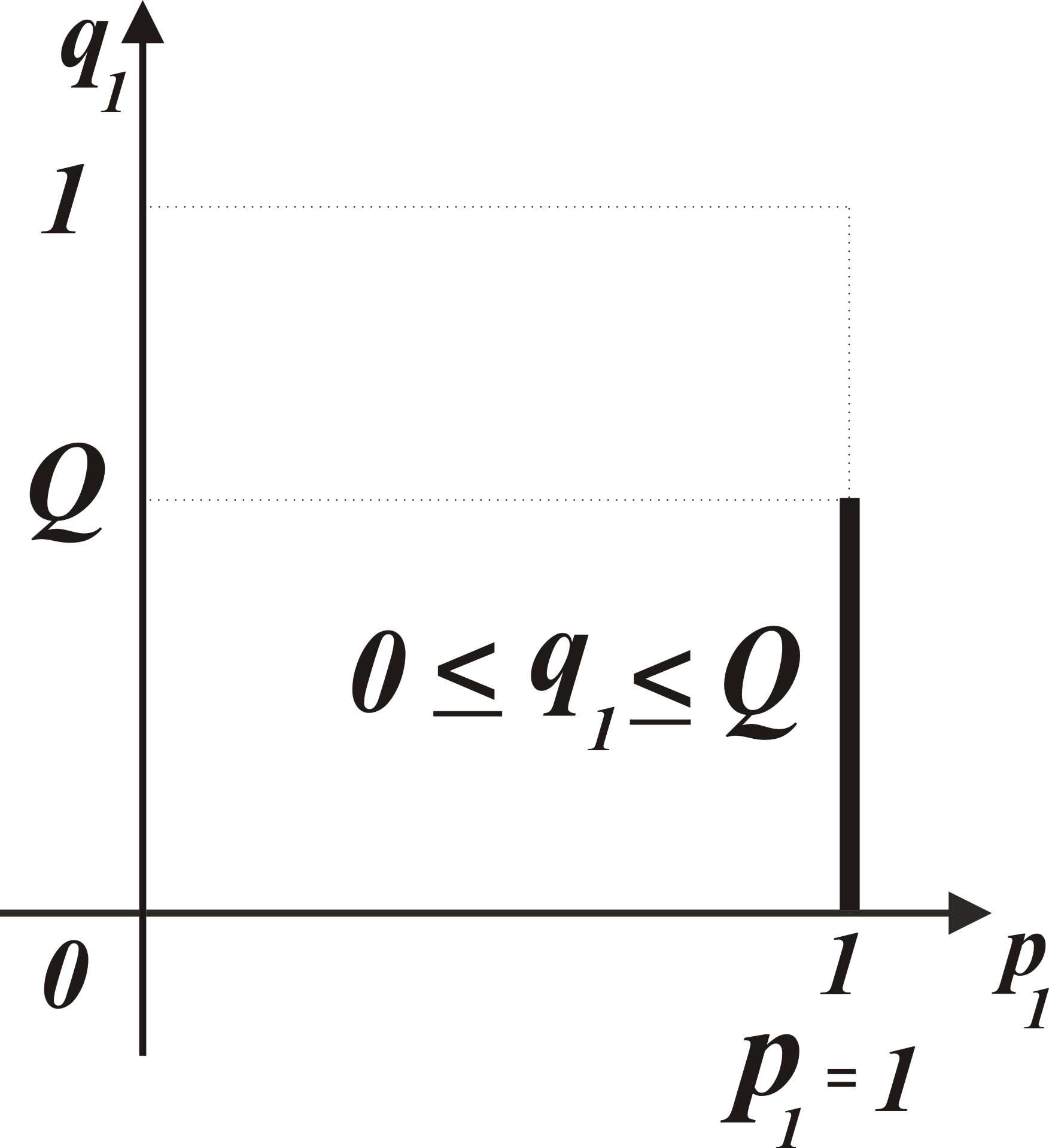
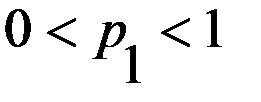 , разделив обе части первого неравенства
, разделив обе части первого неравенства на выражение
на выражение 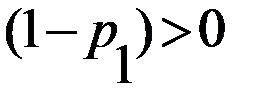 , и обе части второго неравенства
, и обе части второго неравенства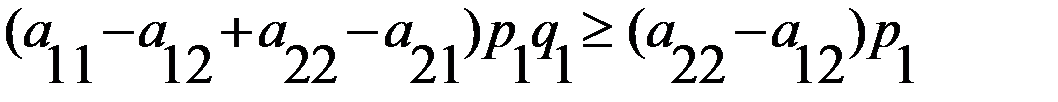 на
на 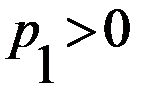 , переходим к одной из следующих систем
, переходим к одной из следующих систем или
или 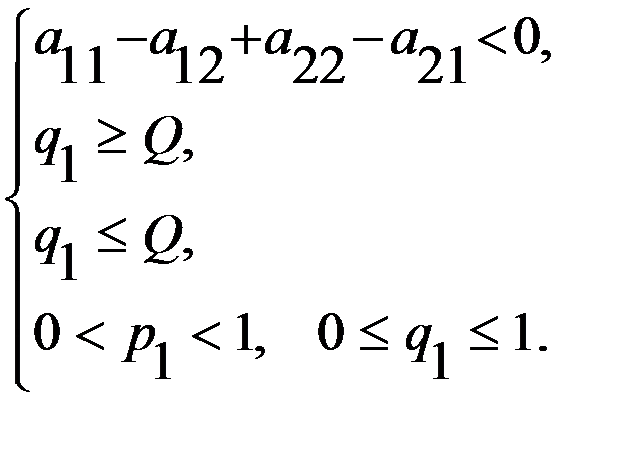
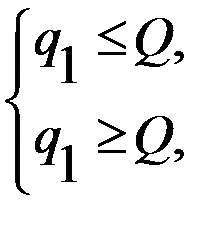 удовлетворяет единственное значение
удовлетворяет единственное значение 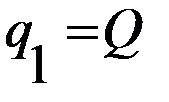 , то, вне зависимости от знака выражения (
, то, вне зависимости от знака выражения (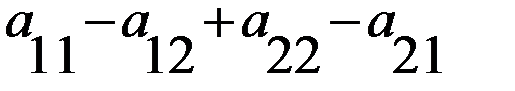 ),
),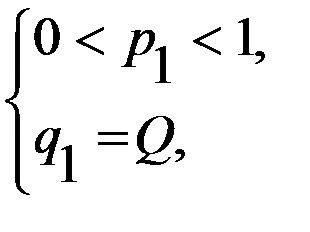 графическое решение которой представлено на рис. 3.5.
графическое решение которой представлено на рис. 3.5.
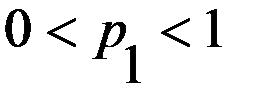 , получаем множество решений для второго игрока,
, получаем множество решений для второго игрока, ,
,  .
.


 = 0 и система принимает вид
= 0 и система принимает вид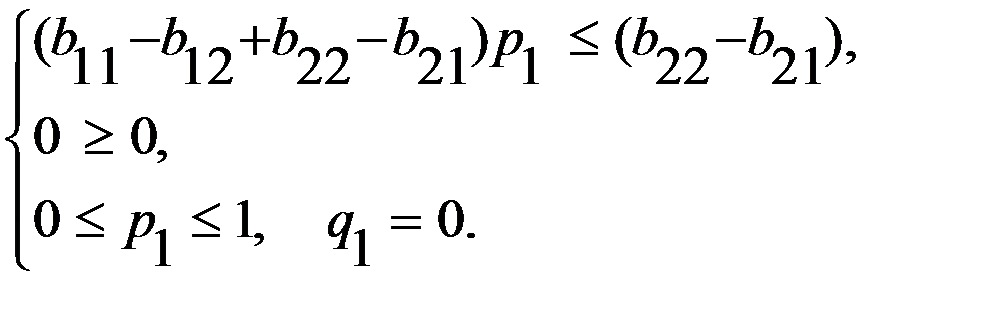
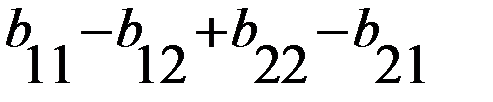 , в зависимости от знака делителя, с учетом обозначения
, в зависимости от знака делителя, с учетом обозначения 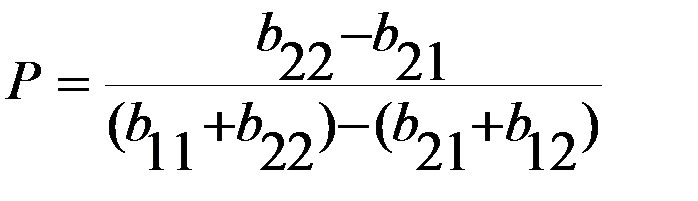 , получим два случая.
, получим два случая.  или
или 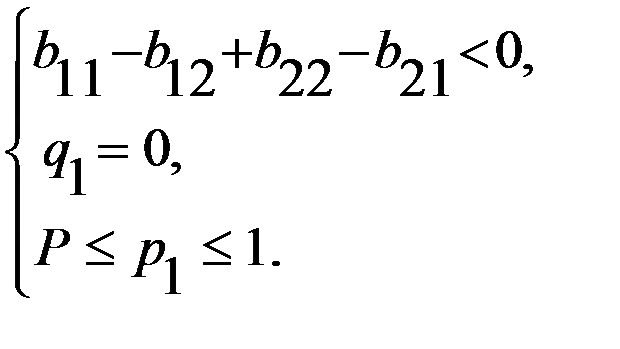
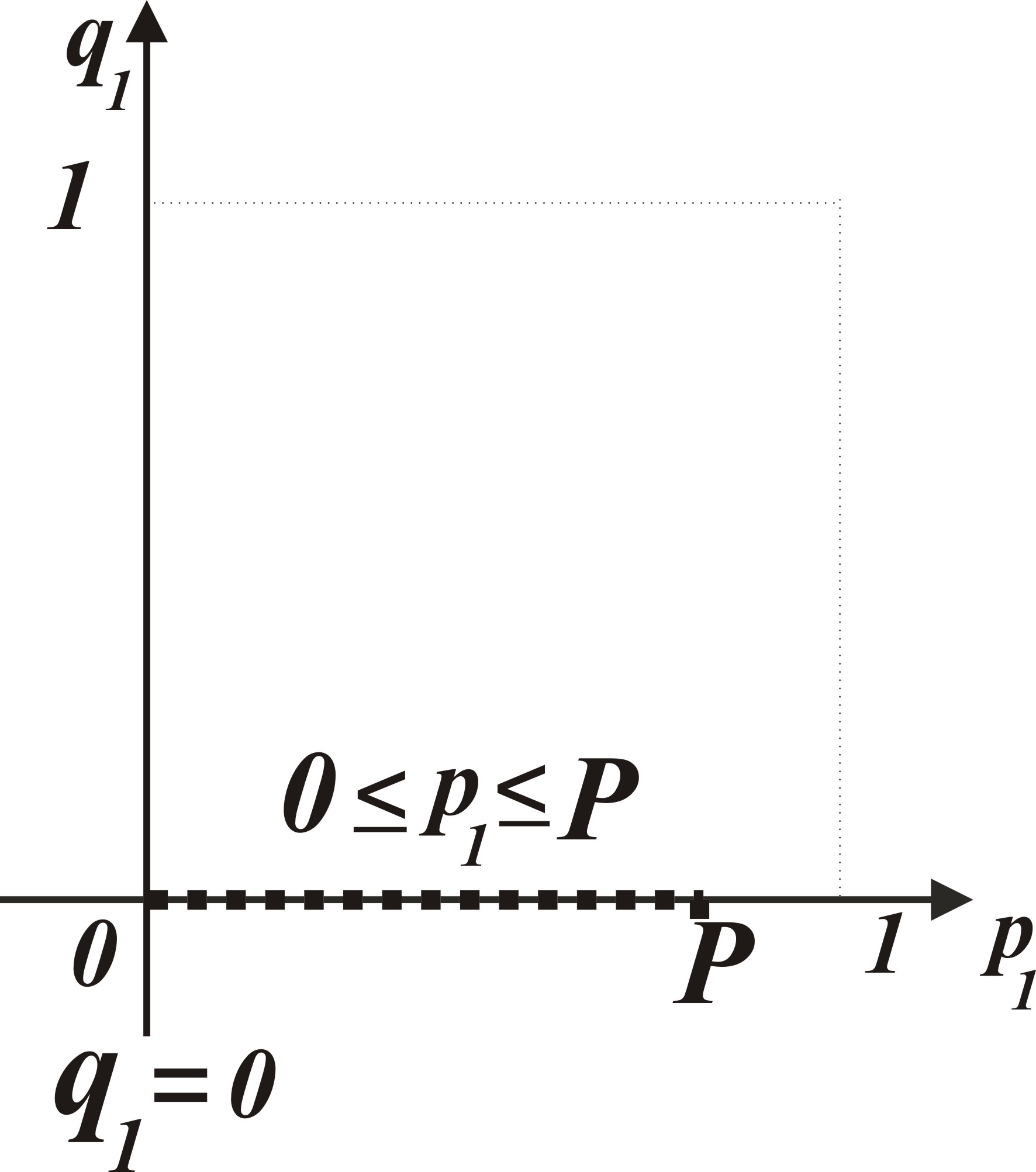

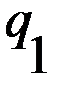 = 1 и система принимает вид
= 1 и система принимает вид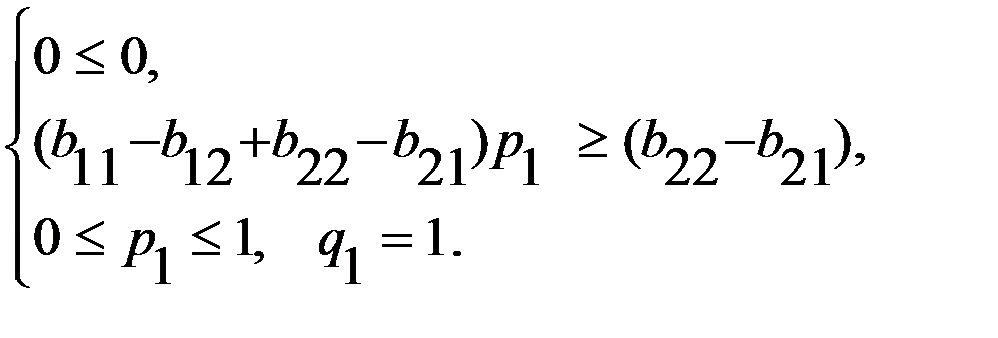
 или
или 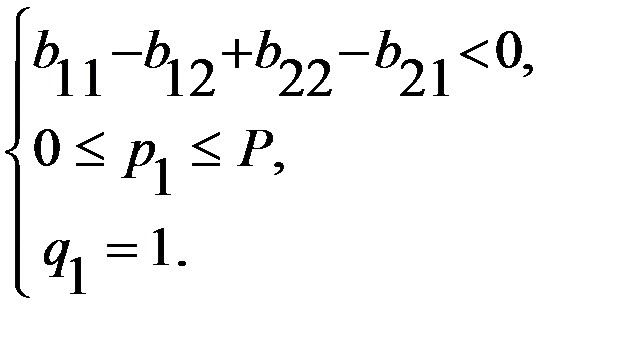


 , разделив обе части первого неравенства
, разделив обе части первого неравенства на выражение
на выражение 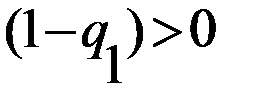 , и обе части второго неравенства
, и обе части второго неравенства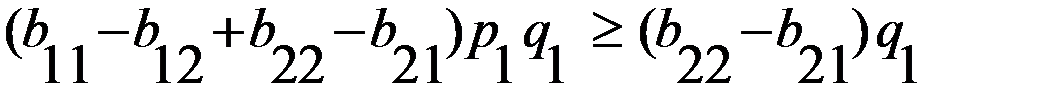 на
на 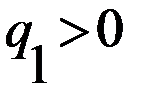 , переходим к одной из следующих систем
, переходим к одной из следующих систем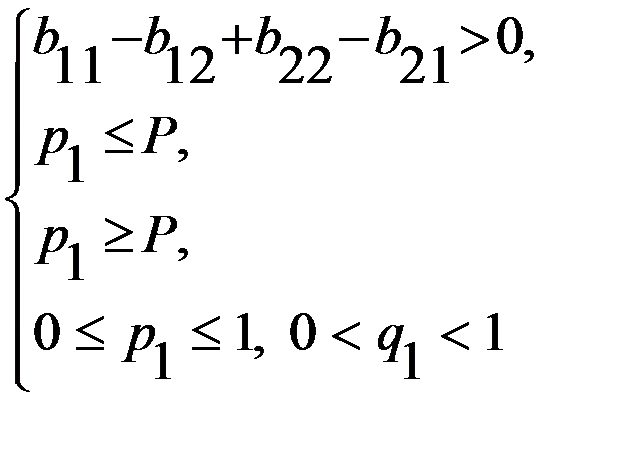 или
или 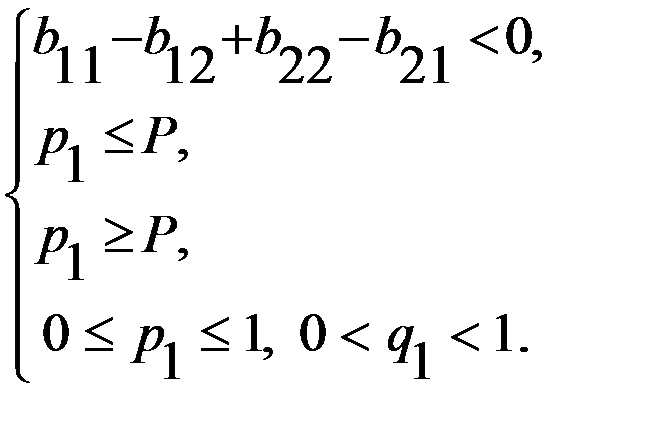
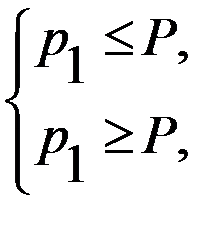 удовлетворяет единственное значение
удовлетворяет единственное значение  .
.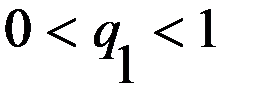 получаем систему
получаем систему 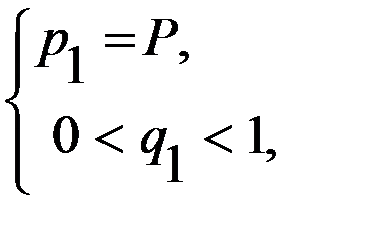 графическое решение которой представлено на рис. 3.12.
графическое решение которой представлено на рис. 3.12.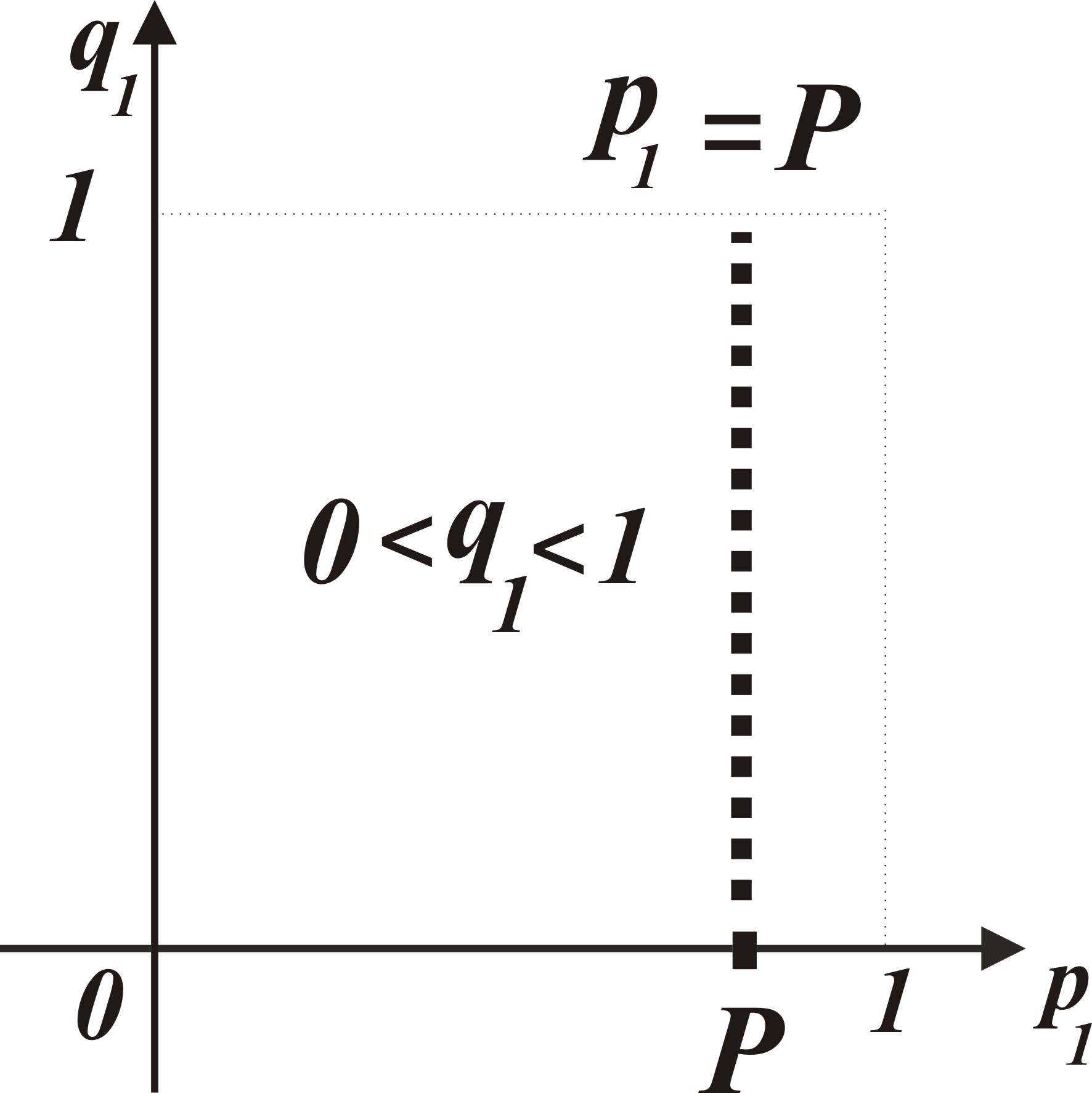
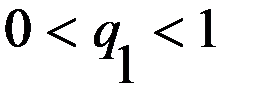 , получаем множество решений для первого игрока,
, получаем множество решений для первого игрока,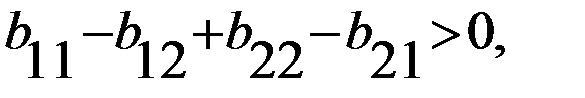
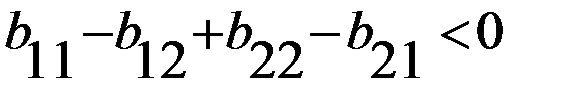 .
.



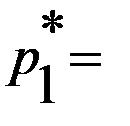
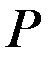 и
и 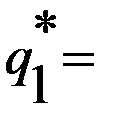
 .
. 


 и
и 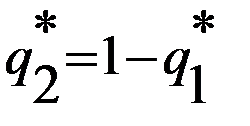 , находим в каждом случае оптимальные смешанные стратегии первого и второго игроков
, находим в каждом случае оптимальные смешанные стратегии первого и второго игроков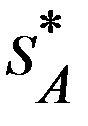 =
=  и
и 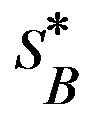 =
=  .
.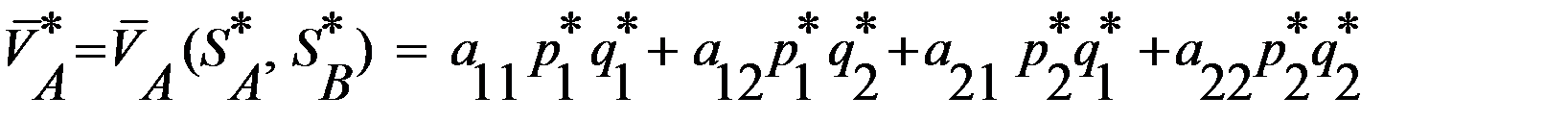 ,
,  .
.


