Динамическое программирование

При решении сложной оптимизационной задачи объем вычислений перебором всех вариантов может оказаться очень большим. В этом случае может помочь метод динамического программирования. Суть его в том, что задача разбивается на этапы и на каждом этапе проводится оптимизация. Но оптимизируется решения не для данного этапа, а для совокупности этого этапа со всеми рассмотренными ранее.

Пример 1. Пусть требуется проложить дорогу из пункта А в пункт В, показанные на схеме на рис.12. Прокладывать следует по линиям сетки. Стоимость прокладки на каждом участке показана. Требуется проложить маршрут так, чтобы стоимость его прокладки была минимальной.

	12	8	13	11	9	14	В
	4	7	5	4	6	5	3
	7	13	11	8	10	10
	7	6	7	6	5	3	5
	10	11	8	13	7	14
	5	3	4	7	4	4	2
	13	10	14	11	10	12
	4	5	6	3	5	5	6
А	10	12	9	14	13	8

Рис.12

Начнем расчет с последнего шага. В пункт В можно попасть из двух соседних пунктов – слева или снизу. В каждом из этих пунктов в кружке напишем стоимость прокладки оставшейся части дороги (14 и 3) и направление ее прокладки.

Затем рассматриваем пункты, отстоящие от конечного на два шага, на первой таблице они обозначены жирными точками. Для каждого из них рассматриваем всевозможные продолжения и стоимость прокладки дороги до конечного пункта по этим продолжениям. Для верхнего и нижнего пунктов, находящихся на границе, продолжения единственные. В соответствующих кружках ставим соответственно 9+14=23 и 5+3=8. В среднем пункте возможны два продолжения. Если двигаться вверх, то получим стоимость 5+14=19, если же двигаться направо – то 10+3=13. Выбираем меньшее, обозначаем направление направо.

	12	8	13	11	9	14	В
	4	7	5	4	6	5	3
	7	13	11	8	10	10
	7	6	7	6	5	3	5
	10	11	8	13	7	14
	5	3	4	7	4	4	2
	13	10	14	11	10	12
	4	5	6	3	5	5	6
А	10	12	9	14	13	8

 

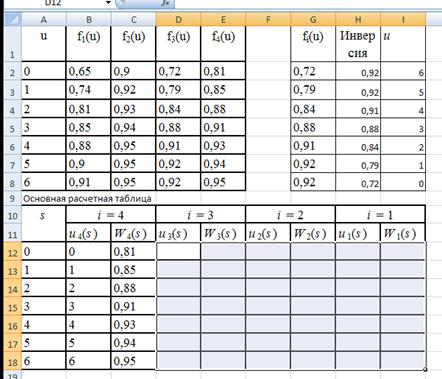
Рис.13

Далее таким же образом заполняем вершины третьего уровня, и т.д. Если в какой-нибудь вершине стоимость по обоим направлениям оказывается одинаковой, направление задаем произвольно. Когда дойдем до начальной вершины А, получим минимальную стоимость прокладки дороги и соответствующую цепочку направлений. Эта цепочка начинается с вершины А и продолжается далее по стрелкам. В нашем случае эта стоимость равна 72.

Оптимальное распределение ресурсов. Имеется некоторое количество ресурсов (материальные, трудовые, финансовые), которые необходимо распределить либо между производственными участками, либо по годам или другим периодам. При этом нужно получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, например, прибыль, себестоимость, суммарные затраты и т.д.

Пример 2. Хозяйство приобрело 6 единиц специализированной техники, которую нужно распределить между четырьмя отделениями с тем, чтобы максимально повысить общий уровень технической готовности. Для каждого i -гоотделения известен уровень технической готовности f_i (u), который отделение будет иметь, если получит u единиц техники. Эти данные приведены в таблице. Оптимизационная задача заключается в том, чтобы сделать максимальной сумму всех уровней.

u	f1(u)	f2(u)	f3(u)	f4(u)
0	0,65	0,90	0,72	0,81
1	0,74	0,92	0,79	0,85
2	0,81	0,93	0,84	0,88
3	0,85	0,94	0,88	0,91
4	0,88	0,95	0,91	0,93
5	0,90	0,95	0,92	0,94
6	0,91	0,95	0,92	0,95

Вычисления будем проводить средствами EXCEL в специальной таблице. Считаем, что техника отправляется последовательно в первое, второе, третье, четвертое отделения. Анализ начинаем с последнего шага, то есть четвертого отделения. Используем следующие параметры:

s – количество нераспределенных единиц техники, оставшихся к данному шагу;

u_i (s) – количество единиц техники, которое может быть выделено i -му отделению (рассматриваемому на данном шаге заполнения таблицы). Это количество выделяется из s нераспределенных, значит, u_i (s) ≤ s.

W_i (s) – максимальный суммарный уровень технической готовности, который достигается при данном значении u_i (s) с учетом всех рассмотренных ранее шагов.

 

s	i = 4		i = 3		i = 2		i = 1
	u 4(s)	W 4(s)	u 3(s)	W 3(s)	u 2(s)	W 2(s)	u 1(s)	W 1(s)
0	0	0,81	0	1,53
1	1	0,85	1	1,60
2	2	0,88
3	3	0,91
4	4	0,93
5	5	0,94
6	6	0,95

При i = 4 столбцы u ₄(s) и W ₄(s) заполняются очень просто. Возможные значения u ₄(s) совпадают с s, так как это последнее отделение и больше распределять технику не придется. Суммарный уровень технической готовности – это уровень технической готовности 4-го отделения, он просто переносится из первой таблицы.

При i = 3 и i = 2 для заполнения столбцов необходимы специальные вычисления. Рассмотрим i = 3. При s = 0 не осталось нераспределенной техники, поэтому u ₃(0) = 0 и W ₃(0) = f ₃(0) + W ₄(0) = 0,72 + 0,81 = 1,53. При всех других значениях s требуется производить сравнение. При s = 1 возможные значения u ₃(0) это 0 или 1. Тогда для 4-го отделения останется соответственно 1 или 0 единиц техники, и суммарный уровень технической готовности будет соответственно f ₃(0) + W ₄(1) = 0,72 + 0,85 = 1,57 и f ₃(1) + W ₄(0) = 0,79 + 0,81 = 1,60. Выбираем большее, делаем вывод, что u ₃(1) = 1 и W ₃(1) = 1,60. Для s = 2 придется сравнивать уже три суммы f ₃(0) + W ₄(2), f ₃(1) + W ₄(1) и f ₃(2) + W ₄(0). Наибольшая из этих сумм принимается за W ₃(2), а соответствующий аргумент при f ₃ – значение u ₃(2).

В общем случае для нахождения u_i (s) и W_i (s) сравниваем суммы

f_i (0) + W_{i- 1}(s), f_i (1) + W_{i- 1}(s – 1), f_i (2) + W_{i- 1}(s – 2), …, f_i (s) + W_{i- 1}(0).  (1)

Выбираем из них максимальную и берем в качестве W_i (s). Соответствующий аргумент при f_i  будет значением u_i (s).

Суммируемые значения находятся в столбцах первой и второй таблицы, причем расположены там в обратном порядке. Это дает возможность организовать вычисления в EXCEL. При этом отметим, что EXCEL только уменьшает объем работы, но для задач большой размерности он все равно будет достаточно большим. Здесь следует использовать специальное программное обеспечение.

Скопируем таблицы WORD на лист EXCEL. Вторая таблица будет основной расчетной таблицей. Создадим вспомогательные таблицы, как показано на рисунке 14.

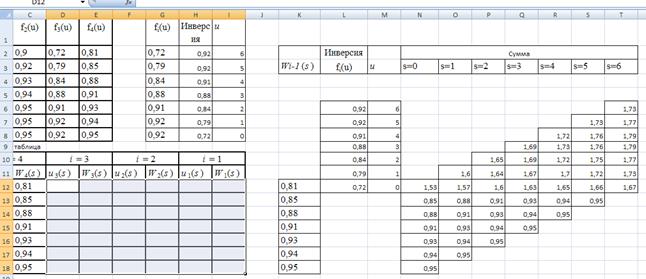
Рис.14

В столбец G вспомогательной таблицы будем копировать соответствующий столбец из первой таблицы, который мы хотим записать в обратном порядке, то есть создать его инверсию. На рис.14 туда отправлен столбец значений f ₃(u). В столбце Н сформируем эту инверсию. Для этого в ячейки Н2 – Н8 введем формулы =$G$8, =$G$7, …, =$G$2. Рядом в столбце I выпишем значения соответствующих значений u.

Теперь создадим расчетную таблицу для вычисления сумм (1). В столбец К скопируем содержимое очередного столбца W_{i- 1}(s) основной расчетной таблицы. На рис.2 мы видим там содержимое столбца W ₄(s). В столбцы L и M скопируем массив G2 – I8 так, чтобы его последняя строка оказалась против первой заполненной числами строки предыдущего столбца.

В столбцах N – T будем вычислять значения сумм (1). В ячейку N12 вводим формулу =K12+L12, протягиваем ее вниз до строки 18 и производим в получившемся массиве команду заменить: K на $ K$ и L на $ L. Этот массив копируем и вставляем в следующие столбцы, сдвигая каждый раз на одну строку выше. В получившихся ячейках и будут вычисляться суммы (1). При этом следует иметь в виду, что нужные нам суммы будут находиться в строках начиная с 12 и выше.

Мы уже имеем возможность заполнить столбцы u ₃(s) и W₃(s) основной расчетной таблицы. Для s = 0 выбирать не приходится, так как сумма единственная. Вносим в основную расчетную таблицу значения u ₃(0) = 0, W₃(0) = 1,53. Эти значения следует набирать вручную, а не копировать, чтобы они не менялись при последующей работе с таблицей.

При s = 1 мы выбираем уже из двух сумм, равных 1,6 и 1,57. Выбираем большую, переносим ее в основную расчетную таблицу вместе с соответствующим значением u = 1. Так же поступаем со всеми следующими суммами. При равенстве двух наибольших значений выбираем любое. В результате столбцы основной расчетной таблицы для i = 3 будут заполнены.

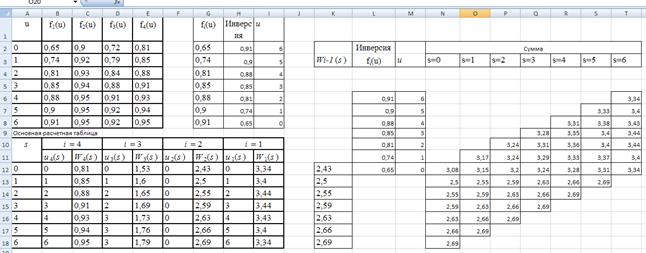
Рис.15

Для i = 2 меняем только содержимое двух массивов. В столбец G копируем значения столбца f ₂(u) первой таблицы, в столбец K – только что полученное содержимое столбца W ₃(s) основной расчетной таблицы. Анализируем образовавшиеся суммы и вносим значения в основную расчетную таблицу так же, как для i = 3.

Так же поступаем для всех остальных значений i, кроме последнего i = 1. Здесь нам уже не придется выбирать для нахождения u ₁(s), так как все нераспределенное к этому шагу достанется первому отделению. Это значит, что u ₁(s) = s. Из всех сумм мы рассматриваем только суммы из последнего столбца для s = 6 и просто переносим получившиеся значения в основную расчетную таблицу.

Рис.16

 

Расчеты закончены. Результат показан на рис.16. Подведем итоги. Видим, что максимальное значение целевой функции W₁(s), равное 3,44, достигается при u ₁(s), равном 3 или 2. Если u ₁(s) = 3, то есть первому отделению достается 3 машины, то остается распределить s = 3 машины. В строке основной таблицы, соответствующей s = 3, в столбце u ₂(s) имеем значение 0, то есть второму отделению не достается машин. Значит, значение u ₃(s) также ищем при s = 3, оно равно 2. Это количество машин достается третьему отделению, и четвертому остается 1 машина.

Если же взять u ₁(s) = 2, то дальше для u ₂(s) придется искать значение в строке s = 4, оно также равно 0. Тогда значение u ₃(s) также ищем при s = 4, оно равно 3. Четвертому отделению опять остается 1 машина.

 

Задания для лабораторных работ

Лабораторная работа 1
«Определение оптимального сочетания зерновых культур»

Определить оптимальное сочетание зерновых культур: пшеницы, ячменя, ржи, овса.

Производство культур характеризуется следующей таблицей:

 

Показатели	Пшеница	Ячмень	Рожь	Овес
Урожайность с 1 га, ц	40	35	36	30
Затраты труда на 1 га, чел.-ч.	20	15	15	13
Затраты удобрений на 1 га, руб.	80	50	60	40

 

Производственные ресурсы:

 

Ресурс	Вариант
	1	2	3	4	5
Пашня, га	2100	1900	2200	1800	2000
Труд, чел.-ч.	36000	32000	39000	30000	34000
Удобрения, руб.	135000	120000	139000	115000	125000

 

Производство продовольственного зерна (пшеница, рожь) – не менее 2000 т, фуражного зерна (ячмень, овес) – не менее 2000 т.

 

Критерий оптимальности: максимальное производство зерна.

Номер варианта - номер студента в списке в журнале.

 

Лабораторная работа 2
«Оптимизация количества удобрений, вносимых в поле»

Выполнить лабораторную работу, описанную в теме  «Решение задачи линейного программирования средствами EXCEL», включив в решение все приведенные зерновые культуры. В качестве параметра а в строке таблицы, где заданы площади под культуры, взять номер студента по списку в журнале.

Лабораторная работа 3
«Распределение удобрений в условиях дефицита»

Выполнить лабораторную работу, описанную в теме  «Задача нелинейного программирования». В качестве параметра а в строке таблицы, где заданы площади под культуры, взять номер студента по списку в журнале.

№	Культура	Озимая пшеница	Яровая пшеница	Рожь	Ячмень	Овес
1	Площадь, га	120 + 10 а	70 + 10 а	110	150 – 10 а	70

 

Лабораторная работа 4
«Оптимизация загрузки машины»

Решите задачу целочисленного программирования.

Предприятие собирается отправить на ярмарку свою продукцию пяти видов на грузовой машине. Грузоподъемность машины 5 т, объем 15 кубометров. Планируется представить не менее двух единиц продукции каждого вида. Рассчитайте, сколько следует взять единиц продукции каждого вида, чтобы она поместилась в машину и ее суммарная стоимость была максимальной. Необходимые параметры представлены в таблице.

В качестве параметра а взять номер студента по списку в журнале.

 

Вид продукции 1 2 3 4 5 Масса, кг 30 100 55 10 80 Объем, куб.м 0,09 1 0,4 0,03 0,5 Цена, руб 1500 11000+100 а 6500 500 8500

 

Лабораторная работа 5
«Многокритериальная задача»

Определить оптимальное сочетание трех зерновых культур: пшеницы, ячменя и овса. Производство культур характеризуют показатели таблицы.

Показатели	Озимая пшеница	Яровой ячмень	Овес
Урожайность с 1 га, ц.	40	35	30
Затраты труда на 1 га, чел.-ч.	20	15	13
Затраты удобрений на 1 га, руб.	80	50	40

Производственные ресурсы: пашня – (1600+100а) га, удобрения – 100000 руб. В качестве параметра а взять номер студента по списку в журнале.

Критерий оптимальности: максимальное производство зерна и минимальные затраты труда.

Решить задачу двумя способами.

1. Считать главным критерием производство зерна. Решить задачу максимизации этого показателя. Получив результат, определить приемлемый уровень сбора зерна. Наложив соответствующее ограничение, решить задачу минимизации затрат труда.

2. Построить целевые функции – производство зерна и затраты труда. Выбрав по своему усмотрению коэффициенты к ним, задать их комбинацию – новую целевую функцию. Решить задачу ее максимизации (или минимизации).

Сравните полученные решения и сделайте выводы.

 

Лабораторная работа 6
«Распределение техники по отделениям хозяйства»

Решите задачу динамического программирования.

Распределить между четырьмя отделениями с тем, чтобы максимально повысить общий уровень технической готовности. Для каждого i-го отделения известен уровень технической готовности f_i(u), который отделение будет иметь, если получит u единиц техники. Эти данные приведены в таблице. Распределить машины таким образом, чтобы суммарный уровень технической готовности был максимальным.

 

u	f1(u)	f2(u)	f3(u)	f4(u)
0	0,63	0,69	0,74	0,81
1	0,73	0,77	0,80	0,86
2	0,80	0,85	0,84	0,89
3	0,85	0,89	0,87	0,91
4	0,88	0,91	0,90	0,92
5	0,90	0,92	0,91	0,93
6	0,91	0,92	0,92	0,94

 

Литература

1. Смиряев, А.В. Моделирование: от биологии до экономики. Учебное пособие./ А.В. Смиряев, А.В. Исачкин, Л.К.Харрасова./ М.: Изд-во МСХА, 2002. – 122 с.

2. Светлов Н.М., Светлова Г.Н. Построение и решение оптимизационных моделей средствами MS Excel и ХА: Методические указания. М.: Изд-во МСХА, 2005.– 27 с.

3. Братусь, А.С.Динамические системы и модели биологии/ А.С. Братусь,  А.С. Новожилов,  А.П. Платонов. М.: Физматлит, 2010. – 398 с.

4. Самарский, А.А. Математическое моделирование: Идеи. Методы. Примеры: Монография/ А.А.Самарский, А.П.Михайлов. – М: Физматлит, 2005. – 320с.

Оглавление

1.  Модели и моделирование 3

2.  Модели в сельском хозяйстве и биологии 4

3.  Задача линейного программирования 7

4.  Решение задачи линейного программирования средствами EXCEL 9

5.  Задача нелинейного программирования 15

6.  Многокритериальные задачи 18

7.  Динамическое программирование 19

8.  Задания для лабораторных работ 24

Лабораторная работа 1 «Определение оптимального сочетания зерновых культур» 24

Лабораторная работа 2 «Оптимизация количества удобрений, вносимых в поле» 25

Лабораторная работа 3 «Распределение удобрений в условиях дефицита» 25

Лабораторная работа 4 «Оптимизация загрузки машины» 25

Лабораторная работа 5 «Многокритериальная задача» 26

Лабораторная работа 6 «Распределение техники по отделениям хозяйства» 26

Литература 27