Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реакция якоря при сдвиге щеток с геометрической нейтрали.Содержание книги
Поиск на нашем сайте
Продольная МДС Fad создает продольный поток Φαd, который может сильно увеличивать или уменьшать результирующий магнитный поток машины Фрез в зависимости от того, совпадает МДС Fad с FB или направлена против нее. Направление определяется тем, в какую сторону сдвинуты щетки. Если щетки сдвинуты по направлению вращения генератора или против направления вращения электродвигателя, то продольная МДС Fad размагничивает машину. При сдвиге щеток в обратном направлении МДС Fad подмагничивает машину. Свойство продольной МДС Fad изменять результирующий магнитный поток Фрез используется в некоторых специальных машинах, например в электромашинных усилителях с поперечным полем. Поперечная МДС Faq создает магнитный поток Фаq; она действует на поток Фрез так же, как и при расположении щеток на геометрической нейтрали. Поток в полюсе состоит из 2 частей. Одна из них поступает в воздушный зазор и формирует поле машины, эта часть является рабочим потоком. Другая часть сцеплена только с витками обмотки возбуждения и косвенно участвует в создании электромагнитного момента. Эту часть потока называют потоком рассеяния. Он зависит от проводимости межполюсного окна
Расчет магнитных цепей H – напряженность магнитного поля, А/м (Ампер/метр); Ф – поток индукции магнитного поля, Вб (Вебер); F = I · w – магнитодвижущая сила (м. д. с.), А (Ампер); Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю. Закон полного тока применяется к замкнутому контуру, образованному средними магнитными линиями магнитной цепи и имеет вид: ∫H→⋅dl→=∑I⋅w,∫H→⋅dl→=∑I⋅w, где ∫H→⋅dl→=∑H⋅l∫H→⋅dl→=∑H⋅l – падение магнитного напряжения UM = H · l в контуре; F=∑I⋅wF=∑I⋅w – магнитодвижущая сила контура (м. д. с.). Второй закон Кирхгофа для магнитных цепей сформулируем следующим образом: алгебраическая сумма магнитных напряжений UM = H · l в замкнутом контуре магнитной цепи (∑UM=∑H⋅l)(∑UM=∑H⋅l) равна алгебраической сумме магнитодвижущих сил F = I · w в том же контуре (∑F=∑I⋅w)(∑F=∑I⋅w): ∑UM=∑F∑UM=∑F
или ∑H⋅l=∑I⋅w.∑H⋅l=∑I⋅w. Задачи на расчет магнитной цепи могут быть двух видов: прямая задача на расчет магнитной цепи – когда задан поток и требуется рассчитать магнитодвижущую силу (м. д. с.) и обратная задача на расчет магнитной цепи – когда по заданной м. д. с. требуется рассчитать магнитный поток. В обоих случаях должны быть известны геометрические размеры магнитной цепи и заданы кривые намагничивания ее материалов. Алгоритм прямой задачи расчета неразветвленной магнитной цепи Дана конфигурация и геометрические размеры неразветвленной магнитной цепи, кривая (или кривые) намагничивания магнитного материала и магнитный поток или индукция магнитного поля в каком-либо сечении. Требуется найти магнитодвижущую силу, ток или число витков намагничивающей обмотки. Расчет проводим в соответствии с алгоритмом: 1. Разбиваем магнитную цепь на однородные (из одного магнитного материала) участки постоянного сечения и определяем длины lk и площади поперечного сечения Sk участков. Длины участков (в метрах) берем по средней силовой линии. 2. Исходя из постоянства потока вдоль всей неразветвленной магнитной цепи, по заданному магнитному потоку Ф и сечениям Sk участков находим магнитные индукции на каждом участке: Bk= Ф Sk.Bk=ФSk. Если задана магнитная индукция на каком-либо участке магнитной цепи, то магнитный поток вдоль всей неразветвленной цепи Ф = Bk · Sk. 3. По найденным магнитным индукциям Bk участков цепи и кривой намагничивания материала k -го участка цепи (например, рис. 2.1, табл. 2.1) определяем напряженности поля Hk на каждом участке магнитной цепи. Напряженность поля в воздушном зазоре находим по формуле H возд =B возд μ0=B возд 4π⋅10−7.Hвозд=Bвоздμ0=Bвозд4π⋅10−7. 4. Подсчитаем сумму падений магнитных напряжений UMk = Hk · lk вдоль всей магнитной цепи ∑UMk=∑Hk⋅lk∑UMk=∑Hk⋅lk и на основании второго закона Кирхгофа для магнитной цепи приравниваем сумме магнитодвижущих сил Fk = Ik · wk вдоль всей магнитной цепи: ∑Hk⋅lk=∑Ik⋅wk.∑Hk⋅lk=∑Ik⋅wk. Основным допущением при расчете является то, что магнитный поток вдоль всей неразветвленной магнитной цепи полагаем неизменным.
Билет 4
Вопрос 1 Высшие гармоники МДС и поля. Составляющая магнитного поля и индуктивные сопротивления обмоток. Гармоники – это синусоидальные волны суммирующиеся с фундаментальной. Вращающееся поле кроме основной (первой) гармонической индукции может содержать в той или иной мере выраженные высшие гармонические. Вращающееся поле, содержащее высшие гармонические, называется несинусоидальным вращающимся полем Полюсное деление МДС высших пространственных гармоник обратно пропорционально номеру гармоники: фv = ф /v. Поэтому пространственная периодичность этих гармоник растет пропорционально номеру гармоники (см. рис. 4.1). Учитывая изложенное, запишем уравнение МДС третьей гармоники фазных обмоток: f3A = F3A sin α1t cos3ß; f3B = F3B sin(α1t - 120)cos3(ß - 120) = F 3A sin (α1t -120)cos3 ß; f3C = F3C sin(α1t- 240)cos3 ß (ß - 240) = F 3A sin (α1t - 240) cos3ß. откуда МДС третьей гармоники трехфазной обмотки f3 = f3A + f3B + f3C = 0, (4-17) т. е. результирующая МДС третьей гармоники в трехфазной обмотке статора при симметричной нагрузке фаз равна нулю. Это распространяется также и на высшие гармоники, кратные трем (9, 15 и др.). МДС высших гармоник оставшихся номеров (5, 7 и др.) ослабляются распределением обмотки в пазах, укорочением шага катушек и скосом пазов. МДС высших гармоник многофазной обмотки статора - вращающиеся. При этом частота их вращения nv в раз меньше частоты вращения МДС основной гармоники: nv = n1/. (4.18) Направление вращения этих МДС зависит от номера гармоники: МДС гармоник порядка 6х + 1 вращаются согласно с МДС основной гармоники -- прямовращающиеся МДС, а МДС порядка 6х - 1 вращаются встречно МДС основной гармоники -- обратновращающиесяМДС (здесь х= 1, 2, 3,...). Магнитное поле* создаваемое током обмотки, подразделяется на три пространственные зоны: 1) поле воздушного зазора, 2) поле пазов и 3) поде лобовых частей обмотки. Полезное действие машины переменного тока, за редким исключением некоторых машин специального назначения, основано на действии магнитного поля основной гармоники воздушного зазора. Это поле поэтому является главным, или рабочим, а поля пазов и лобовых частей — полями рассеяния. К последним относятся также поля высших гармоник воздушного зазора, которые называются полями рассеяния воздушного зазора или полями дифференциального рассеяния. Второе название обусловлено тем, что эти поля представляют собой разность между полным полем воздушного зазора и его основной гармоникой. Таким образом, магнитное поле рассеяния состоит из трех главных частей: 1) пазового, 2) лобового и 3) поля рассеяния воздушного зазора, или дифференциального.
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.1.159 (0.01 с.) |

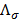 и от МДС
и от МДС 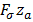 и возрастает с увеличением насыщения магнитной цепи.
и возрастает с увеличением насыщения магнитной цепи.