
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание дискретной случайной величиныСодержание книги
Поиск на нашем сайте Одна из самых важных числовых характеристик случайной величины есть математическое ожидание. Если известна дискретная случайная величина
то математическим ожиданием (или средним значением) дискретной величины
Таким образом, математическое ожидание дискретной случайной величины Пример 1. Найти математическое ожидание случайной величины
Свойства математического ожидания. 1. Постоянный множитель можно выносить за знак математического ожидания:
2. Математическое ожидание постоянной величины С равно самой этой величине:
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин:
Среднее квадратичное отклонение и дисперсия случайной величины. Пример 2. Найдем математическое ожидание случайных величин 1)
2)
Решение:
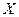 и и 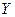 разные, а их математические ожидания одинаковы. разные, а их математические ожидания одинаковы.
Из рисунка б видно, что значение величины Основной числовой характеристикой степени рассеяния значений случайной величины Определение. Отклонением называется разность между случайной величиной Отклонение Определение. Дисперсией дискретной случайной величины
Свойства дисперсии. 1. Дисперсия постоянной величины С равна 0:
2. Если
3. Если
Для вычисления дисперсий более удобной является формула
Пример 3. Дискретная случайная величина распределена по закону:
Найти Решение. Сначала находим
а затем
По формуле
Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:
Практическая работа №10 «Решение простейших задач теории вероятностей и математической статистики»
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.151.90 (0.007 с.) |

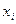
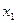
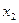
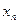
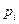
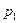
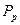
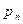
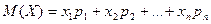 .
.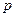
 .
.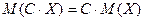
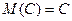
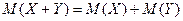 .
.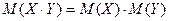 .
.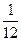
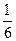
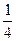
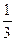
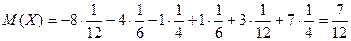 ,
,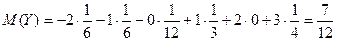 .
.
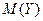 , чем значения величины
, чем значения величины 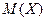 (рисунок а).
(рисунок а).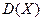 .
.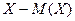 .
.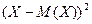 также являются случайными величинами.
также являются случайными величинами.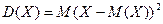 .
.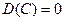 .
.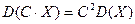
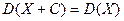 .
.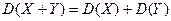 .
.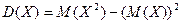 .
.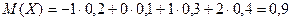 ,
,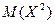 .
.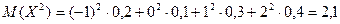 .
.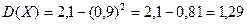 .
.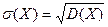 .
.


