Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как вычислить определенный интеграл по формуле Симпсона.
И снова, начнём с общей формулы. Рассмотрим определенный интеграл На практике отрезков может быть: Итак, наше разбиение имеет следующий вид: Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
Пример. Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков Решение: Начинаем решать. Если у нас два отрезка разбиения Вычислим шаг разбиения: Заполним расчетную таблицу: В результате: Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: Вычислим шаг разбиения: Заполним расчетную таблицу: Найдём абсолютное значение разности между приближениями: Так как Формула Симпсона: Вычислим шаг: И снова заполним расчетную таблицу: Таким образом: Заметьте, что здесь вычисления желательно уже расписать более подробно, поскольку формула Симпсона достаточно громоздкаОцениваем погрешность: Погрешность меньше требуемой точности:
Ответ: Метод прямоугольников. Вычислить определённый интеграл Решение: Вычислим шаг разбиения (длину каждого промежуточного отрезка): Метод левых прямоугольников получил своё называние из-за того, Вычислим площадь ступенчатой фигуры, которая равна сумме площадей прямоугольников: При использовании «правого» метода высОты прямоугольников равны значениям функции в правых концах промежуточных отрезков: Запишем формулы в общем виде. Если функция В чём их формальное различие? В первой формуле нет слагаемого На практике рассчитываемые значения ПР№8. «Приближенное вычисление по формулам прямоугольников, трапеции, Симпсона»
ТЕМА 9 Задачи, приводящие к дифференциальным уравнениям. Задача Коши. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами
Обыкновенным дифференциальным уравнением 1 -го порядка называется выражение вида Решением дифференциального уравнения называется такая функция у=у(х), которая при подстановке ее в это уравнение обращает его в верное тождество. Общим решением дифференциального уравнения 1-го порядка называется такое его решение
где числа Решение уравнения , удовлетворяющее начальному условию (4), называется решением задачи Коши и записывается в виде Решить задачу Коши (5) означает найти интегральную кривую дифференциального уравнения, которая проходит через заданную точку Примеры. Пример№1: Решить дифференциальные уравнения: а) Решение: а) Приведём уравнение к виду Интегрируем обе части уравнения: Ответ: б) Приведём уравнение к виду: разделим обе части уравнения на Переменные разделены. Интегрируем обе части уравнения:
Применим основное логарифмическое тождество получим
При делении на Ответ: Пример №2: Найдите решения задачи Коши: а) Решение: а)
Интегрируем обе части уравнения:
Подставим начальное условие в общее решение, получим
Так как по условию Ответ: б)
Интегрируем обе части уравнения:
Так как по условию Ответ:
Решите следующие задачи. 1. Решите дифференциальные уравнения: а) г) 2. Найдите решения задачи Коши: а) б)
Дифференциальное уравнение второго порядка, содержит: Решить дифференциальное уравнение – это значит, найти множество функций
2.Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение: По какому принципу составлено характеристическое уравнение, отчётливо видно:
Существуют три варианта развития событий. Если характеристическое уравнение
Пример. Решить дифференциальное уравнение Решение: составим и решим характеристическое уравнение:
Ответ: общее решение:
|
|||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.27.178 (0.04 с.) |
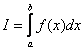 , где
, где  – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 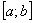 . Проведём разбиение отрезка
. Проведём разбиение отрезка 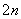 .
.
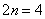

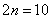
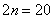
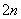 понимается как ЕДИНОЕ ЧИСЛО. То есть, НЕЛЬЗЯ сокращать, например,
понимается как ЕДИНОЕ ЧИСЛО. То есть, НЕЛЬЗЯ сокращать, например,  . Запись
. Запись 
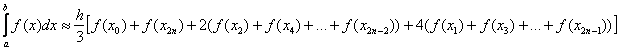 , где:
, где: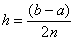 – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг;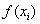 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках 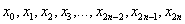 .
.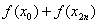 – сумма первого и последнего значения подынтегральной функции;
– сумма первого и последнего значения подынтегральной функции;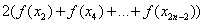 – сумма членов с чётными индексами умножается на 2;
– сумма членов с чётными индексами умножается на 2; – сумма членов с нечётными индексами умножается на 4.
– сумма членов с нечётными индексами умножается на 4.
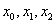 . И формула Симпсона принимает весьма компактный вид:
. И формула Симпсона принимает весьма компактный вид:



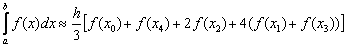
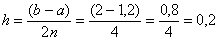

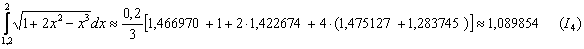
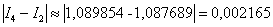
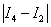 больше требуемой точности:
больше требуемой точности:  , то необходимо еще раз удвоить количество отрезков:
, то необходимо еще раз удвоить количество отрезков: 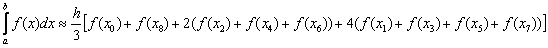
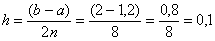

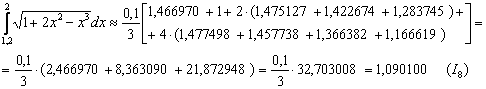
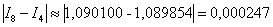
 . Осталось взять наиболее точное приближение
. Осталось взять наиболее точное приближение 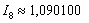 , округлить его до трёх знаков после запятой и записать:
, округлить его до трёх знаков после запятой и записать: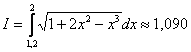 с точностью до 0,001
с точностью до 0,001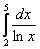 приближённо:
приближённо: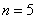 равных отрезков, результаты вычислений округлять до 0,001
равных отрезков, результаты вычислений округлять до 0,001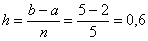

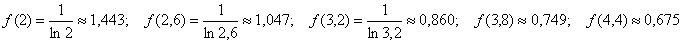 Ни в коем случае не забываем, что округление следует проводить до трёх знаков после запятой – это существенное требование условия.
Ни в коем случае не забываем, что округление следует проводить до трёх знаков после запятой – это существенное требование условия.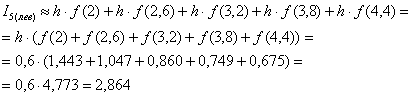
 . Совершенно понятно, что, рассмотрев бОльшее количество промежуточных отрезков (измельчив разбиение), ступенчатая фигура будет гораздо больше похожа на криволинейную трапецию, и мы получим лучший результат.
. Совершенно понятно, что, рассмотрев бОльшее количество промежуточных отрезков (измельчив разбиение), ступенчатая фигура будет гораздо больше похожа на криволинейную трапецию, и мы получим лучший результат.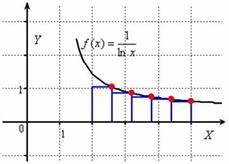
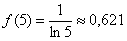 и площадь ступенчатой фигуры:
и площадь ступенчатой фигуры: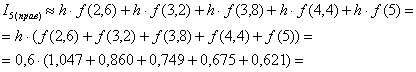
 – тут, что и следовало ожидать, приближение сильно занижено:
– тут, что и следовало ожидать, приближение сильно занижено: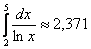
 равных частей:
равных частей: 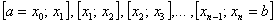 , то определённый интеграл
, то определённый интеграл  можно вычислить приближенно по формулам:
можно вычислить приближенно по формулам: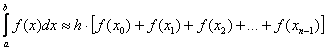 – левых прямоугольников;
– левых прямоугольников;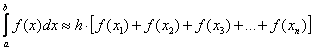 – правых прямоугольников;
– правых прямоугольников; – шаг разбиения.
– шаг разбиения. , а во второй -
, а во второй - 

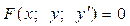 , т.е. уравнение, содержащее неизвестную, искомую функцию y=y(x) и ее производную.
, т.е. уравнение, содержащее неизвестную, искомую функцию y=y(x) и ее производную.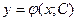 , которое является функцией переменной х и произвольной независимой постоянной С. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
, которое является функцией переменной х и произвольной независимой постоянной С. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).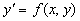 Определение: Задача нахождения решения уравнения , удовлетворяющего
Определение: Задача нахождения решения уравнения , удовлетворяющего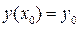 условию (4)
условию (4) 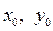 – заданные числа, называется задачей Коши. Условие (4) называется начальным условием.
– заданные числа, называется задачей Коши. Условие (4) называется начальным условием.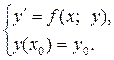 . (5)
. (5)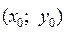 .
.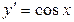 ; б)
; б) 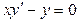 .
.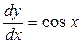 ;
; 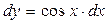 .
.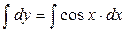 ;
; 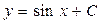 .
. .
. ;
; 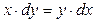 .
. :
:  .
.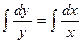 ;
; 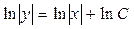 .
.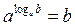 или
или  ,
,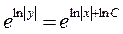 или
или  .
.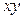 могли быть потеряны решения
могли быть потеряны решения 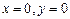 . Очевидно, что
. Очевидно, что 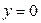 является решением данного уравнения при C=0, а
является решением данного уравнения при C=0, а  – нет. Таким образом, формула
– нет. Таким образом, формула  , где С – произвольная постоянная, задаёт все решения данного уравнения.
, где С – произвольная постоянная, задаёт все решения данного уравнения. .
. 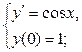 б)
б) 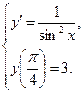
 Найдём общее решение дифференциального уравнения.
Найдём общее решение дифференциального уравнения.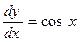 ;
; 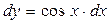 .
.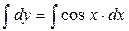 ;
; 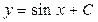 .
.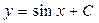 – общее решение дифференциального уравнения.
– общее решение дифференциального уравнения.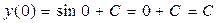 .
. , то С=1. Тогда частное решение данного дифференциального уравнения имеет вид
, то С=1. Тогда частное решение данного дифференциального уравнения имеет вид 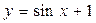 .
.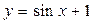 .
.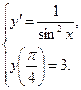 Найдём общее и частное решение дифференциального уравнения.
Найдём общее и частное решение дифференциального уравнения.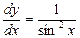 ;
; 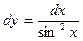 .
. ;
; 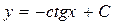 .
.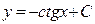 – общее решение дифференциального уравнения. Подставим начальное условие в общее решение, получим
– общее решение дифференциального уравнения. Подставим начальное условие в общее решение, получим  .
. , то –1+С=3, С=4. Тогда частное решение данного дифференциального уравнения имеет вид
, то –1+С=3, С=4. Тогда частное решение данного дифференциального уравнения имеет вид  .
. .
.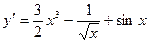 ; б)
; б) 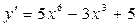 ; в)
; в) 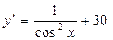 ;
;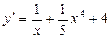 ; д)
; д) 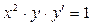 ; е)
; е)  .
. в)
в)  д)
д) 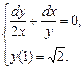
 г)
г) 
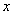 ;
;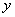 (функцию);
(функцию);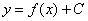 , которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения. , где
, где  и
и 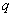 – константы (числа), а в правой части – строго ноль.
– константы (числа), а в правой части – строго ноль.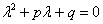
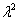 ;
;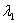 ,
,  (т.е., если дискриминант
(т.е., если дискриминант 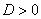 ), то общее решение однородного уравнения выглядит так:
), то общее решение однородного уравнения выглядит так: , где
, где 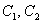 – константы.
– константы.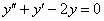

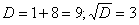
 ,
,