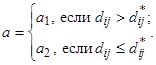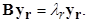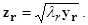Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Получение и интерпретация графических отображений
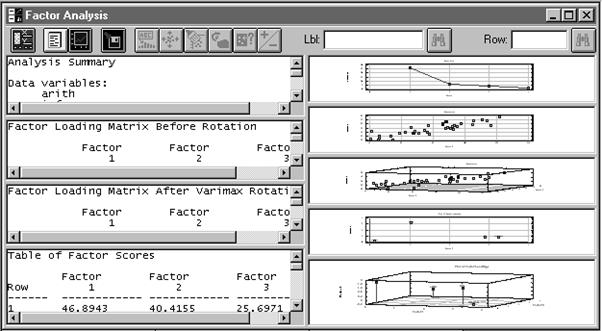
Нажмем кнопку графических опций (третья слева). Появится соответствующее окно диалога. Щелкнем на кнопке All, задействуя все графические опции. Система добавит на рабочее поле 5 окон с различными графическими отображениями результатов факторного анализа (Рис. 7. 13).
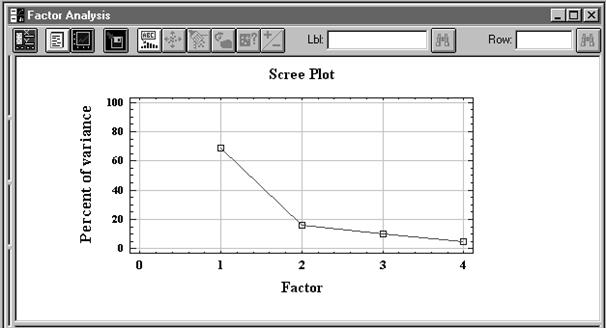
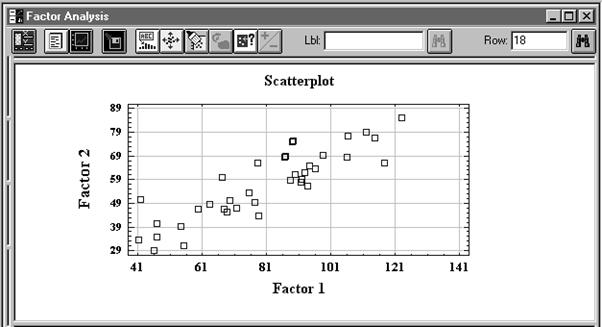
Рис. 7. 13. Все табличные и графические окна факторного анализа Раскроем сначала окно c названием Scree Plot. Этот график в исходном построении иллюстрирует собственные значения для каждого фактора. Но, предположим, нам хочется иметь выражения величины собственных значений в процентах. Щелкнем на графике правой кнопкой мыши и получим окно диалога для задания опций данного вида отображения результатов факторизации. Установим флажок Percent of Variance (процент дисперсии) вместо Eigenvalues (собственные значения). Заметим, что фактор 1 имеет весьма высокое и, конечно, самое большое значение процента дисперсии. На фактор 2 приходится менее 20 % дисперсии, а фактор 4 и вовсе малозаметен по этому показателю (Рис. 7. 14). Минимизируем размеры рассмотренного графика. Дважды щелкнем левой кнопкой мыши на втором графическом окне 2D Scatterplot (двухмерная диаграмма рассеивания). На полученном рисунке показана проекция исследуемых объектов на плоскость, образованную первым и вторым факторами. Судя по конфигурации облака точек, первый и второй факторы сильно коррелируют. То есть в нашем случае, применительно к пожилым людям с выраженными признаками старения, общий интеллект у них тесно связан со способностью к произведению в уме арифметических действий (Рис. 7. 15)
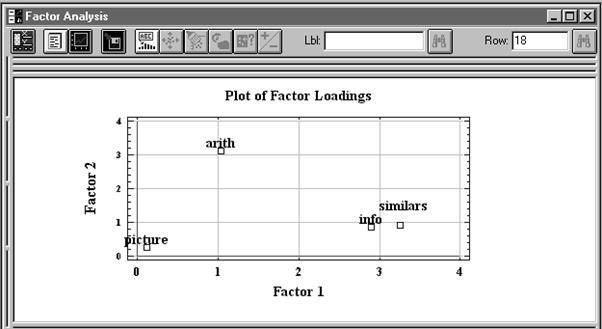
Рис. 7. 14. Иллюстрация процента дисперсии для выделенных факторов Вернем двухмерной диаграмме рассеивания прежние минимальные размеры, дважды щелкнув на ней левой кнопкой мыши. Максимизируем размеры графического отображения 3D Scatterplot. Этот график представляет собой проекцию объектов в трехмерное пространство, образованное первыми тремя факторами. Свернем рассмотренное отображение. Дважды щелкнем левой кнопкой мыши на графике 2D Factor Plot (двумерное отображение факторных нагрузок), раскрывая график на все рабочее поле (Рис. 7. 16) На графике хорошо видно, что переменная arith имеет значение как для первого, так и для второго факторов. Вместе с тем у переменной picture малые нагрузки на все факторы, а тестовые измерения info и similars имеют большие нагрузки только на первый фактор.
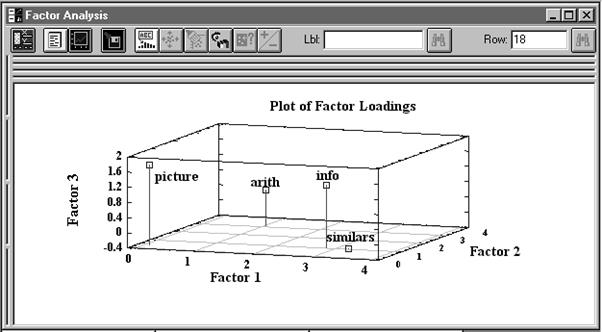
Свернем раскрытое окно до минимальных размеров, дважды щелкнув на нем левой кнопкой мыши. Раскроем до максимальных размеров окно 3D Factor Plot (трехмерный факторный график). График изображает факторные нагрузки уже в пространстве трех факторов (Рис. 7. 17).
Рис. 7. 15. Проекция объектов на плоскость первого и второго факторов
Рис. 7. 16. Графическое изображение факторных нагрузок
Рис. 7. 17. Отображение факторных нагрузок в пространстве трех факторов Из приведенного рисунка видно, что весьма высокую нагрузку имеет переменная picture. Однако, эта нагрузка приходится на третий выделенный фактор, а, как нам известно из предыдущих данных, третий фактор играет несущественную роль при описании рассмотренных экспериментальных наблюдений. Нелинейные отображения Нелинейные методы отображения данных в пространство меньшей размерности, как правило, пренебрегают аналитическим выражением преобразования исходного пространства признаков в новые координатные оси, позволяющим интерпретировать новое координатное пространство. Они не скованы никакими ограничениями на вид допустимых преобразований. Все операции подчинены одной главной цели: построить графическое изображение совокупности данных, дающее наиболее наглядное представление об особенностях их структуры. Причем особенности структуры понимаются достаточно широко. Это приводит к тому, что алгоритмы нелинейного отображения могут быть направлены не обязательно на минимальное искажение всех попарных расстояний между объектами выборки в исходном пространстве признаков, а, например, на максимально точное отображение только сравнительно больших расстояний или наоборот, только малых. Такая гибкость методов нелинейного отображения позволяет настраивать их на тот или иной интересующий аспект структуры данных и как бы целенаправленно зондировать изучаемую выборку. Для получения нелинейных отображений y (x) задается некоторый критерий (мера) искажения структуры данных J { y (x)} и решается задача на определение минимума J. Большинство мер искажения основано на сравнении попарных расстояний между объектами в исходном пространстве
где
Если в приведенном критерии положить a < 0, то он станет более чувствительным к ошибкам отображения малых расстояний и менее чувствительным к искажению больших расстояний. При a > 0, наоборот, точнее отображаются большие расстояния и загрубляются малые, так критерий начинает сильнее реагировать на ошибки в передаче больших расстояний Обычно результаты, полученные для a < 0 лучше, чем для a > 0 /Айвазян С. А. и др., 1989/. Несколько более разнообразные возможности предоставляет использование двухпараметрического критерия, предложенного в /Терехина А. Ю., 1986/,
Данный критерий может оказаться полезным, если при отображении объектов в Поиск отображений объектов в пространство меньшей размерности, минимизирующих значение критерия J, осуществляется, как правило, с помощью различных градиентных процедур. Большой выбор таких процедур для решения данной задачи, а также разнообразные варианты критерия J предлагаются, например в /Попечителев Е. П. и др., 1985; Терехина А. Ю., 1986/. В качестве начального приближения для новых координат объектов часто используются их проекции на первые главные компоненты. Размерность пространства для визуального анализа данных в Многомерное шкалирование Многомерное шкалирование — совокупность методов, позволяющих по заданной информации о мерах различия (близости) между объектами рассматриваемой совокупности приписывать каждому из этих объектов вектор характеризующих его количественных показателей. При этом размерность искомого координатного пространства задается заранее, а «погружение» в него анализируемых объектов производится таким образом, чтобы структура взаимных различий (близостей) между ними, измеренных с помощью приписываемых им вспомогательных координат, в среднем наименее отличалась бы от заданной в смысле того или иного функционала качества /Айвазян С. А., и др., 1989/.Процедуры многомерного шкалирования отличаются от описанных выше методов линейного и нелинейного проецирования данных в пространство меньшей размерности в основном тем, что исходной информацией для них служит только матрица различий (близостей) между исследуемыми объектами и не требуется знания значений признаков для этих объектов. Когда информация задана в виде матрицы попарных расстояний между объектами, используются методы так называемого метрического шкалирования. Если же элементы матрицы выражают порядковые отношения между объектами, то применяются методы неметрического шкалирования. Ниже охарактеризован классический подход к решению задачи метрического шкалирования.
Обычно, хотя и не обязательно, пространство Метод определения координат точек x1, …, x N (с точностью до ортогонального вращения) и заодно размерности пространства, в которое они отображаются, основан не на непосредственном использовании матрицы D, а на преобразовании ее в матрицу B скалярных произведений центрированных векторов
где m — вектор средних значений. Между элементами матрицы B и расстояниями dij установлено следующее соотношение
Процедура перехода от D к B называется двойным центрированием D. Матрица B размера (N ´ N) обладает следующими свойствами: a) Неотрицательно определена. b) Ранг матрицы B равен размерности искомого пространства отображения. c) Ненулевые собственные числа матрицы B, упорядоченные в порядке убывания, совпадают с соответствующими собственными числами матрицы S = XX T, где X — центрированная матрица данных (неизвестная нам). Матрица S / N есть матрица ковариаций для X. d) Пусть ur есть r‑ й собственный вектор матрицы S,соответствующий r‑ му собственному числу lr. Тогда вектор значений r ‑й главной компоненты будет zr = X T ur. В то же время пусть yr — r ‑й собственный вектор матрицы B, соответствующий тому же самому собственному значению lr, то есть
Тогда
Из свойства 4 следует, что, решая задачу собственных чисел и собственных векторов для матрицы B и ограничиваясь ненулевыми собственными числами l 1, …, lp’, получаем координатное представление точек в пространстве главных компонент, основываясь на приведенных формулах. Элементы матрицы B могут быть представлены в виде
Очевидно, решение Z является линейной функцией X и определяется лишь с точностью до ортогонального преобразования, поскольку, применяя к матрице Z преобразование вращения, получим, что преобразованная матрица Z * столь же точно восстанавливает матрицу B, как и матрица Z. Поэтому такое шкалирование называют линейным.
Подробно с классическим подходом к многомерному шкалированию можно ознакомиться в работах /Torgerson W. S., 1952; Терехина А. Ю., 1986; Дэйвисон М., 1988/. Решение задачи шкалирования, полученное классическим линейным методом, часто используется как начальное приближение в процедурах нелинейного многомерного шкалирования, которые строятся аналогично рассмотренным выше процедурам нелинейного проецирования данных в пространство меньшей размерности. Особенности этих процедур описаны в приведенной литературе по многомерному шкалированию.
|
||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 83; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.147 (0.014 с.) |
 и пространстве отображения
и пространстве отображения 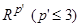 . Например, используется мера, предложенная в /Sammon J. W., 1969/ и являющаяся аналогом критерия «стресса», применяемого в многомерном шкалировании,
. Например, используется мера, предложенная в /Sammon J. W., 1969/ и являющаяся аналогом критерия «стресса», применяемого в многомерном шкалировании,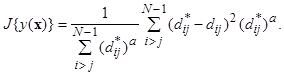
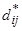 — расстояние между i -м и j -м объектами в исходном пространстве
— расстояние между i -м и j -м объектами в исходном пространстве 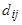 — евклидово расстояние между отображениями этих объектов в
— евклидово расстояние между отображениями этих объектов в 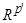 .
.