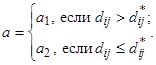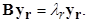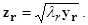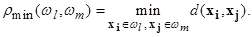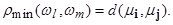Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Урок 7. Методы исследования структуры данныхСтр 1 из 6Следующая ⇒
Урок 7. Методы исследования структуры данных Анализ многомерных данных без использования обучающей информации направлен на выяснение структуры взаимоотношений объектов и признаков ТЭД. В настоящее время накоплен обширный арсенал средств такого анализа. Наиболее полное изложение применяемых здесь подходов, сопровождающееся подробными ссылками на ключевые работы, содержится в /Айвазян С. А. и др., 1989/. Классификация известных методов анализа структуры многомерных данных приведена в табл. 7. 1. Таблица 7. 1. Классификация методов анализа структуры данных
Разделение методов носит достаточно условный характер, так как различные методы имеют немало пересечений в отдельных приемах обработки информации. В основу приведенной классификации положен признак, отражающий степень участия экспериментатора в выделении особенностей взаимоотношений между исследуемыми объектами и признаками. Если в методах автоматического группирования это участие минимально, применение методов визуализации данных нацелено на поиск наиболее выразительных изображений совокупности исследуемых объектов для последующего максимального задействования потенциала зрительного анализатора экспериментатора. Рассмотрим указанные методы более подробно. Методы визуализации данных Основное назначение рассматриваемой группы методов — дать визуальное представление о структуре изучаемых данных. Визуализация данных предполагает получение тем или иным способом графического отображения совокупности объектов на числовую ось, на плоскость или в трехмерный объем, максимально отражающего особенности распределения этих объектов в многомерном пространстве. Пример применения метода главных компонент Ниже рассматривается пример, относящийся к сравнительному оцениванию изделий, характеризующихся одновременно несколькими параметрами. Это — автомобили. В таблице приводятся выборочные сведения о фирме-изготовителе автомобиля, названии модели, а также оценочные параметры — вес (переменная weight), число цилиндров (переменная cylinders), ускорение (переменная accel), объем двигателя (переменная displace) и мощность в лошадиных силах (переменная horspower).
Таблица 7. 2
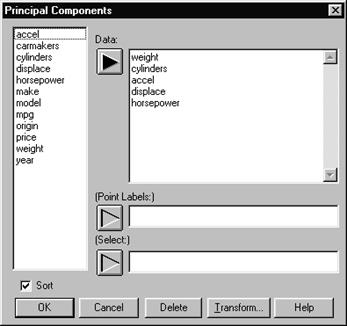
Введем эти данные в электронную таблицу STATGRAPHICS (в ней присутствуют также другие дополнительные параметры). Назовем файл данных cardata. Выберем Special | Multivariate Methods | Principal Components. Появляется окно диалога для задания анализируемых переменных (Рис. 7. 1).
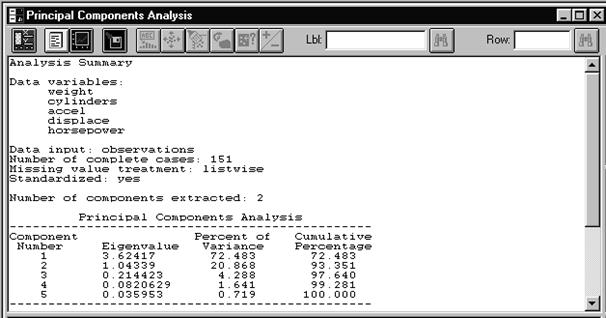
Рис. 7. 1. Окно задания переменных для анализа по методу главных компонент Нажимаем OK. Получаем исходную сводку анализа МГК (Рис. 7. 2). Из полученной сводки заключаем, что анализу подвергаются переменные weight, cylinders, accel, displace и horspower, и что число объектов составляет 151. Далее следует информация непосредственно МГК: собственные значения главных компонент, упорядоченные по величине (Eigenvalue); процент дисперсии, приходящийся на каждую выделенную главную компоненту (Percent of Variance); накопленный процент дисперсии (Cumulative Percentage). Приведенные цифры говорят о том, что уже первые две главные компоненты описывают 93,4 % дисперсии исходных данных. Третья главная компонента добавляет еще приблизительно 4,2 % дисперсии, так что в сумме это получается 97, 6% дисперсии.
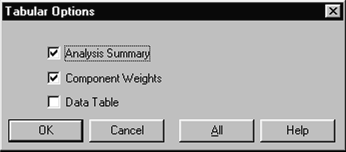
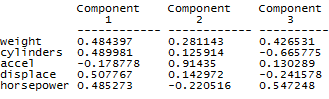
Для более детального анализа нажмем кнопку табличных опций (вторая слева в верхнем ряду) и в соответствующем окне диалога (Рис. 7. 3) установим флажок компонентных весов (Component Weights). Получим следующую таблицу (Рис. 7. 4).
Рис. 7. 2. Исходная сводка МГК
Рис. 7. 3. Окно диалога табличных опций МГК
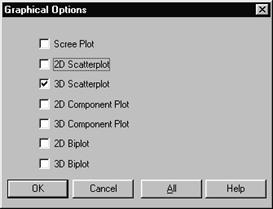
Рис. 7. 4. Веса признаков в главных компонентах Как следует из полученных цифр, в первой главной компоненте примерно одинаковые по величине положительные коэффициенты имеют: вес, количество цилиндров, объем двигателя и мощность в лошадиных силах. Вместе с тем, во второй главной компоненте превалирует только одна величина: ускорение. А в третьей главной компоненте наблюдается сочетание веса машины и ее мощности (с положительным знаком), которому противопоставляется количество цилиндров (с отрицательным знаком). Не углубляясь в интерпретацию полученных главных компонент, которая, конечно, может представлять интерес для специалистов, перейдем к рассмотрению диаграммы рассеивания всей совокупности автомашин в пространстве выделенных трех первых главных компонент. Для этого щелкнем левой кнопкой мыши на кнопке графических опций и инициализируем данное трехмерное отображение.
Рис. 7. 5. Графические опции метода главных компонент
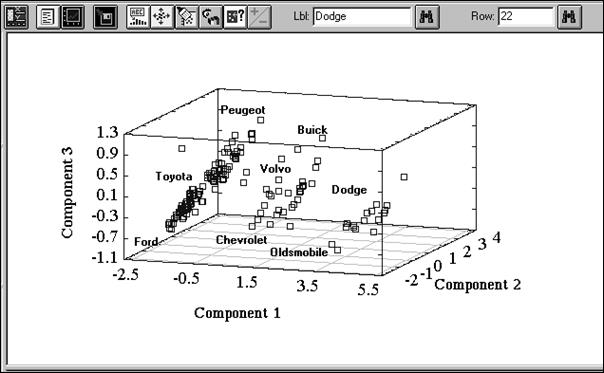
Рис. 7. 6. Проекция исследуемых автомобилей в пространство первых трех ГК На представленном рисунке хорошо видно, что вся исследуемая совокупность автомашин разделилась на три достаточно четко выраженные группы. Для большей выразительности на рисунке даны названия некоторых фирм, производящих автомобили, которые выдаются в специальных окнах STATGRAPHICS после нажатия пятой справа кнопки в верхнем ряду и маркировки интересующей точки. Для первой наиболее многочисленной группировки характерны сравнительно небольшие: вес, количество цилиндров, мощность и объем двигателя (первая слева группа). Вместе с тем, большая доля автомашин этой группы обладают хорошим ускорением (высокие значения 2‑й ГК) и высоким соотношением веса и мощности к количеству цилиндров (3‑я ГК). Вторая группировка не столь многочисленна, но для нее также свойственны указанные характеристики, хотя и менее ярко выраженные. И, наконец, третья группа автомашин (сравнительно малочисленная) имеет большой вес, мощность, количество, цилиндров. В то же время, показатели ускорения и соотношение веса и мощности к количеству цилиндров здесь (если говорить в целом) гораздо меньшие.
Таким образом, произведенный анализ данных с помощью метода главных компонент позволяет получить более «объемное» видение современного автомобильного рынка, что может способствовать лучшей ориентации как потребителей этой продукции, так и производителей с позиций оценки существующих тенденций. Факторный анализ. В отличие от метода главных компонент факторный анализ основан не на дисперсионном критерии автоинформативности системы признаков, а ориентирован на объяснение имеющихся между признаками корреляций. Основная модель факторного анализа записывается следующей системой равенств /Налимов В. В., 1971/
То есть полагается, что значения каждого признака xi могут быть выражены взвешенной суммой латентных переменных (простых факторов) fj, количество которых меньше числа исходных признаков, и остаточным членом ei с дисперсией s 2(ei), действующей только на xi, который называют специфическим фактором. Коэффициенты lij называются нагрузкой i -й переменной на j -й фактор или нагрузкой j -го фактора на i -ю переменную. В самой простой модели факторного анализа считается, что факторы fj взаимно независимы и их дисперсии равны единице, а случайные величины ei тоже независимы друг от друга и от какого-либо фактора fj. Максимально возможное количество факторов m при заданном числе признаков p определяется неравенством
которое должно выполняться, чтобы задача не вырождалась в тривиальную. Данное неравенство получается на основании подсчета степеней свободы, имеющихся в задаче /Лоули Д. и др., 1967/. Сумму квадратов нагрузок называют общностью соответствующего признака xi и чем больше это значение, тем лучше описывается признак xi выделенными факторами fj. Общность есть часть дисперсии признака, которую объясняют факторы. В свою очередь, дисперсия признака = общность Основное выражение факторного анализа показывает, что коэффициент корреляции любых двух признаков xi и xj можно выразить суммой произведения нагрузок некоррелированных факторов
Задачу факторного анализа нельзя решить однозначно. Равенства в факторной модели не поддаются непосредственной проверке, так как p исходных признаков задается через (p + m) других переменных — простых и специфических факторов. Поэтому представление корреляционной матрицы факторами, как говорят ее факторизацию можно произвести бесконечно большим числом способов. Если удалось произвести факторизацию корреляционной матрицы с помощью некоторой матрицы факторных нагрузок F, то любое линейное ортогональное преобразование F (ортогональное вращение) приведен к такой же факторизации /Налимов В. В., 1971/. Поэтому нередко в одном и том же пакете программ анализа данных реализовано сразу несколько версий методов факторизации, и у исследователей возникает закономерный вопрос, какой из них лучше. Здесь сошлемся на слова одного из основоположников современного факторного анализа Г. Хартмана: «Ни в одной из работ не было показано, что какой-либо один метод приближается к ²истинным² значениям общностей лучше, чем другие методы… Выбор среди группы методов наилучшего производится в основном с точки зрения вычислительных удобств, а также склонностей и привязанностей исследователя, которому тот или иной метод казался более адекватным его представлениям об общности» /цит. по Александров В. В. и др., 1990/.
В настоящее время одними из наиболее популярных являются три метода вращения факторов: варимакс, квартимакс и эквимакс. Вращение методом варимакс ставит целью упростить столбцы факторной матрицы, сводя все значения к 1 или 0. Вращение методом квартимакс ставит целью аналогичное упрощение только по отношению к строкам факторной матрицы. И, наконец, эквимакс занимает промежуточное положение — при вращении факторов по этому методу одновременно делается попытка упростить и столбцы и строки. Кроме перечисленных трех методов нередко осуществляют вращение факторов до тех пор, пока не получатся результаты, поддающиеся содержательной интерпретации. Можно, например, потребовать, чтобы один фактор был нагружен преимущественно признаками одного типа, а другой — признаками другого типа. Или, скажем можно потребовать, чтобы исчезли какие-то трудно интерпретируемые нагрузки с отрицательными знаками. Нередко исследователи идут дальше и рассматривают прямоугольную систему факторов как частный случай косоугольной, то есть ради содержания жертвуют условием некоррелированности факторов. В целом по факторному анализу можно отметить следующее. С помощью такого анализа снижение размерности достигается за счет существования групп взаимосвязанных признаков, которые агрегируются в строящихся факторах. Как и при использовании метода главных компонент, полезные сведения о структуре данных можно почерпнуть на основании визуального анализа проектов объектов в одно-, двух- и трехмерные пространства, образованные комбинациями различных факторов. Также ценную информацию о структуре исследуемой выборки могут дать результаты факторного анализа, проведенного раздельно в различных подгруппах объектов. Другие методы линейного проецирования данных, развиваются в рамках направления, получившего название разведочный анализ данных /Тьюки Дж., 1981/. Современные методы проецирования, в частности методы целенаправленного проецирования, являются естественным обобщением охарактеризованных выше классических методов анализа данных. Их систематизация и характеристики представлены в /Айвазян С. А. и др., 1989/. Пример применения факторного анализа Факторный анализ широко применяется в экономике, социологии, медицине для выявления скрытых закономерностей в данных. Но, может быть, наиболее широко он используется в психологии, из которой собственно идут корни факторной статистической техники. Этим объясняется выбор нижеследующего примера, связанного с изучением структуры интеллекта на основе данных, полученных с помощью психологического тестирования. Настоящий пример адаптирован по данным, приведенным в отчете об изучении пожилых людей /Morrison D. F., 1990/. Испытуемые были разбиты с помощью теста Векслера на две полярные группы. Для первой группы характерно наличие признаков старения, для второй такие признаки отсутствуют. В нашем случае будут рассмотрены 37 человек, у которых признаки старения выражены. Мы выделим (на основе экспериментальных данных) факторы и проинтерпретируем их. Откроем файл данных с названием Senile.sf. Таблица 7. 3. Таблица с экспериментальными данными
Нелинейные отображения Нелинейные методы отображения данных в пространство меньшей размерности, как правило, пренебрегают аналитическим выражением преобразования исходного пространства признаков в новые координатные оси, позволяющим интерпретировать новое координатное пространство. Они не скованы никакими ограничениями на вид допустимых преобразований. Все операции подчинены одной главной цели: построить графическое изображение совокупности данных, дающее наиболее наглядное представление об особенностях их структуры. Причем особенности структуры понимаются достаточно широко. Это приводит к тому, что алгоритмы нелинейного отображения могут быть направлены не обязательно на минимальное искажение всех попарных расстояний между объектами выборки в исходном пространстве признаков, а, например, на максимально точное отображение только сравнительно больших расстояний или наоборот, только малых. Такая гибкость методов нелинейного отображения позволяет настраивать их на тот или иной интересующий аспект структуры данных и как бы целенаправленно зондировать изучаемую выборку. Для получения нелинейных отображений y (x) задается некоторый критерий (мера) искажения структуры данных J { y (x)} и решается задача на определение минимума J. Большинство мер искажения основано на сравнении попарных расстояний между объектами в исходном пространстве
где
Если в приведенном критерии положить a < 0, то он станет более чувствительным к ошибкам отображения малых расстояний и менее чувствительным к искажению больших расстояний. При a > 0, наоборот, точнее отображаются большие расстояния и загрубляются малые, так критерий начинает сильнее реагировать на ошибки в передаче больших расстояний Обычно результаты, полученные для a < 0 лучше, чем для a > 0 /Айвазян С. А. и др., 1989/. Несколько более разнообразные возможности предоставляет использование двухпараметрического критерия, предложенного в /Терехина А. Ю., 1986/,
Данный критерий может оказаться полезным, если при отображении объектов в Поиск отображений объектов в пространство меньшей размерности, минимизирующих значение критерия J, осуществляется, как правило, с помощью различных градиентных процедур. Большой выбор таких процедур для решения данной задачи, а также разнообразные варианты критерия J предлагаются, например в /Попечителев Е. П. и др., 1985; Терехина А. Ю., 1986/. В качестве начального приближения для новых координат объектов часто используются их проекции на первые главные компоненты. Размерность пространства для визуального анализа данных в Многомерное шкалирование Многомерное шкалирование — совокупность методов, позволяющих по заданной информации о мерах различия (близости) между объектами рассматриваемой совокупности приписывать каждому из этих объектов вектор характеризующих его количественных показателей. При этом размерность искомого координатного пространства задается заранее, а «погружение» в него анализируемых объектов производится таким образом, чтобы структура взаимных различий (близостей) между ними, измеренных с помощью приписываемых им вспомогательных координат, в среднем наименее отличалась бы от заданной в смысле того или иного функционала качества /Айвазян С. А., и др., 1989/.Процедуры многомерного шкалирования отличаются от описанных выше методов линейного и нелинейного проецирования данных в пространство меньшей размерности в основном тем, что исходной информацией для них служит только матрица различий (близостей) между исследуемыми объектами и не требуется знания значений признаков для этих объектов. Когда информация задана в виде матрицы попарных расстояний между объектами, используются методы так называемого метрического шкалирования. Если же элементы матрицы выражают порядковые отношения между объектами, то применяются методы неметрического шкалирования. Ниже охарактеризован классический подход к решению задачи метрического шкалирования. Обычно, хотя и не обязательно, пространство Метод определения координат точек x1, …, x N (с точностью до ортогонального вращения) и заодно размерности пространства, в которое они отображаются, основан не на непосредственном использовании матрицы D, а на преобразовании ее в матрицу B скалярных произведений центрированных векторов
где m — вектор средних значений. Между элементами матрицы B и расстояниями dij установлено следующее соотношение
Процедура перехода от D к B называется двойным центрированием D. Матрица B размера (N ´ N) обладает следующими свойствами: a) Неотрицательно определена. b) Ранг матрицы B равен размерности искомого пространства отображения. c) Ненулевые собственные числа матрицы B, упорядоченные в порядке убывания, совпадают с соответствующими собственными числами матрицы S = XX T, где X — центрированная матрица данных (неизвестная нам). Матрица S / N есть матрица ковариаций для X. d) Пусть ur есть r‑ й собственный вектор матрицы S,соответствующий r‑ му собственному числу lr. Тогда вектор значений r ‑й главной компоненты будет zr = X T ur. В то же время пусть yr — r ‑й собственный вектор матрицы B, соответствующий тому же самому собственному значению lr, то есть
Тогда
Из свойства 4 следует, что, решая задачу собственных чисел и собственных векторов для матрицы B и ограничиваясь ненулевыми собственными числами l 1, …, lp’, получаем координатное представление точек в пространстве главных компонент, основываясь на приведенных формулах. Элементы матрицы B могут быть представлены в виде
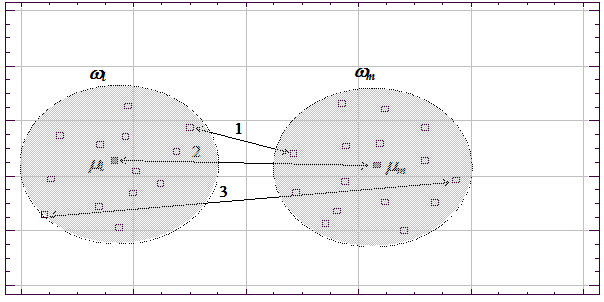
Очевидно, решение Z является линейной функцией X и определяется лишь с точностью до ортогонального преобразования, поскольку, применяя к матрице Z преобразование вращения, получим, что преобразованная матрица Z * столь же точно восстанавливает матрицу B, как и матрица Z. Поэтому такое шкалирование называют линейным. Подробно с классическим подходом к многомерному шкалированию можно ознакомиться в работах /Torgerson W. S., 1952; Терехина А. Ю., 1986; Дэйвисон М., 1988/. Решение задачи шкалирования, полученное классическим линейным методом, часто используется как начальное приближение в процедурах нелинейного многомерного шкалирования, которые строятся аналогично рассмотренным выше процедурам нелинейного проецирования данных в пространство меньшей размерности. Особенности этих процедур описаны в приведенной литературе по многомерному шкалированию. Факторный анализ объектов. При факторном анализе объектов используется формальный аппарат факторного анализа, изначально предназначавшийся для агрегирования взаимосвязанных признаков. Этому аппарату была дана характеристика в предыдущем подразделе. Отличие состоит в том, что в факторном анализе объектов таблица экспериментальных данных поворачивается на 90 0 (транспонируется), то есть объекты и признаки меняются местами. Если при факторном анализе признаков ищутся группы близких (коррелированных) признаков на основе корреляционной матрицы, то для транспонированных данных аналогом корреляционной матрицы является матрица, описывающая попарные коэффициенты корреляции (сходства) объектов. Она вводится в алгоритм формального факторного анализа, и в результате получаются факторы, описывающие уже не группы коррелированных признаков, а группы сходных объектов /Александров В. В. и др., 1990/. Особенности данной процедуры подробно рассмотрены в /Айвазян С. А. и др., 1974/. Кластерный анализ. Этот анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации (cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством). Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования /Миркин Б. Г., 1980/: a) внутри групп объекты должны быть тесно связаны между собой; b) объекты разных групп должны быть далеки друг от друга; c) при прочих равных условиях распределения объектов по группам должны быть равномерными. Требования a) и b) выражают стандартную концепцию компактности классов разбиения /Аркадьев А. Г. и др., 1971/; требование c) состоит в том, чтобы критерий не навязывал объединения отдельных групп объектов. Узловым моментом в кластерном анализе считается выбор метрики (или меры близости объектов), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения /Айвазян С. А. и др., 1989/. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы исследуемой информации и т.п. Другой важной величиной в кластерном анализе является расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний, характеризующих взаимное расположение отдельных групп объектов. Пусть wl — l ‑я группа (класс, кластер) объектов, Nl — число объектов, образующих группу, вектор ml — среднее арифметическое объектов, входящих в wl (другими словами «центр тяжести» l -й группы), а r (wl, wm ) — расстояние между группами wl и wm.
Рис. 7. 18. Различные способы определения расстояния между кластерами: 1 — по ближайшим объектам, 2 — по центрам тяжести, 3 — по самым дальним объектам Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:
Расстояние центров тяжести равно расстоянию между центральными точками кластеров
Расстояние дальнего соседа — расстояние между самыми дальними объектами кластеров
Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояние центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы. Нацеленность алгоритмов кластерного анализа на определенную структуру группировок объектов в пространстве признаков может приводить к неоптимальным или даже неправильным результатам, если гипотеза о типе группировок неверна. В случае отличия реальных распределений от гипотетических указанные алгоритмы часто «навязывают» данным не присущую им структуру и дезориентируют исследователя. Поэтому экспериментатор, учитывающий данный факт в условиях априорной неопределенности прибегает к применению батареи алгоритмов кластерного анализа и отдает предпочтение какому либо выводу на основании комплексной оценки результатов работы этих алгоритмов. Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. Вместе с тем, большинство таких алгоритмов состоит из двух этапов. На первом этапе задается начальное (возможно, искусственное или даже произвольное) разбиение множества объектов на классы и определяется некоторый математический критерий качества автоматической классификации. Затем, на втором этапе, объекты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться. Многообразие алгоритмов кластерного анализа обусловлено также множеством различных критериев, отражающих те или иные аспекты качества автоматического группирования. Простейший критерий качества непосредственно базируется на величине расстояния между кластерами. Однако такой критерий не учитывает «населенность» кластеров — относительную плотность распределения объектов внутри выделяемых группировок. Поэтому другие критерии основываются на вычислении средних расстояний между объектами внутри кластеров. Но наиболее часто применяют критерии в виде отношений показателей «населенности» кластеров к расстоянию между ними. Это, например, может быть отношение суммы межклассовых расстояний к сумме внутриклассовых (между объектами) расстояний или отношение общей дисперсии данных к сумме внутриклассовых дисперсии и дисперсий центров кластеров. Функционалы качества и конкретные алгоритмы автоматической классификации (группирования) достаточно полно и подробно рассмотрены в /Айвазян С. А. и др., 1989/. Иерархическое группирование Процедуры иерархического типа предназначены для получения наглядного представления о стратификационной структуре всей исследуемой совокупности объектов. Эти процедуры основаны на последовательном объединении кластеров (агломеративные процедуры) и на последовательном разбиении (дивизимные процедуры). Наибольшее распространение получили агломеративные процедуры. Они выглядят следующим образом. На первом шаге все объекты считаются отдельными кластерами. Затем на каждом шаге два ближайших кластера объединяются в один. Каждое объединение уменьшает число кластеров на один так, что в конце концов все объекты объединяются в один кластер. Наиболее подходящее разбиение выбирает чаще все
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.51.3 (0.11 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
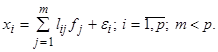
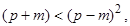
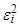 показывает, какая часть дисперсии исходного признака остается необъясненной при используемом наборе факторов, и данную величину называют специфичностью признака. Таким образом,
показывает, какая часть дисперсии исходного признака остается необъясненной при используемом наборе факторов, и данную величину называют специфичностью признака. Таким образом,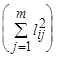 + специфичность
+ специфичность 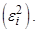
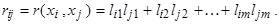
 и пространстве отображения
и пространстве отображения 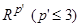 . Например, используется мера, предложенная в /Sammon J. W., 1969/ и являющаяся аналогом критерия «стресса», применяемого в многомерном шкалировании,
. Например, используется мера, предложенная в /Sammon J. W., 1969/ и являющаяся аналогом критерия «стресса», применяемого в многомерном шкалировании,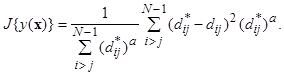
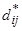 — расстояние между i -м и j -м объектами в исходном пространстве
— расстояние между i -м и j -м объектами в исходном пространстве 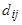 — евклидово расстояние между отображениями этих объектов в
— евклидово расстояние между отображениями этих объектов в 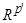 .
.