
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевод чисел из восьмеричной системы счисления в десятичную
Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики: X8 = An ∙ 8n – 1 + An – 1 ∙ 8n – 2 + An – 2 ∙ 8n – 3 +... + A2 ∙ 81 + A1 ∙ 80. Для перевода восьмеричного числа 254 в десятичную систему, согласно правилу, необходимо каждый разряд исходного числа умножить на 8n (n – номер разряда): 2548 = 2 ∙ 82 + 5 ∙ 81 + 4 ∙ 80 = 128 + 40 + 4 = 17210. Пример. Число 75 0138 перевести в десятичную систему счисления: 75 0138 = 7 ∙ 84 + 5 ∙ 83 + 0 ∙ 82 + 1 ∙ 81 + 3 ∙ 80 = 31 24310. Перевод чисел из шестнадцатеричной системы счисления в десятичную. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики: X16 = An ∙ 16n – 1 + An – 1 ∙ 16n – 2 + An – 2 ∙ 16n – 3 +... + A2 ∙ 161 + A1 ∙ 160. Пример. Число FDA116 перевести в десятичную систему счисления: FDA116 = 15 ∙ 163 + 13 ∙ 162 + 10 ∙ 161 + 1 ∙ 160 = 64 92910. Перевод дробных чисел в различные системы счисления Перевод простой десятичной дроби в другие позиционные системы счисления. При переводе правильной десятичной дроби в другую систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножить на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывают как последовательность полученных целых частей произведения. Умножение производят до тех поp, пока дробная часть произведения не станет равной нулю. Перевод осуществляют до заданной точности. Пример. Перевести число 0,35 из десятичной системы: а) в двоичную, б) восьмеричную, в) шестнадцатеричную: Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916. Перевод чисел из различных систем счисления в десятичную систему При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в развернутой форме. Примеры: Разряды 3 2 1 0 -1 Число 1 0 1 1, 12= 1 ∙ 23 + 1 ∙ 21 + 1 ∙ 20 + 1 ∙ 2–1 = 11,510. Разряды 2 1 0 -1 Число 2 7 6, 58 = 2 ∙ 82 + 7 ∙ 81 + 6 ∙ 80 + 5 ∙ 8–1 = 190,62510. Разряды 2 1 0 -1 Число 1 F 3, 416 = 1 ∙ 162 + 15 ∙ 161 + 3 ∙ 160 + 4 ∙ 16-1 = 499,2510.
Перевод из 2-й в 8-ю и 16-ю системы счисления и обратно. Перевод чисел из двоичной в другие системы счисления Перевод чисел двоичной системы счисления в восьмеричную. Для перевода многозначного числа из двоичной системы в восьмеричную его нужно разбить влево и вправо от запятой на триады (тройки цифр), начиная с младшего разряда, и каждую такую группу (триаду) двоичных цифр заменить соответствующей восьмеричной цифрой; недостающее число разрядов дополнить нулями. Например:
Для удобства перевода следует использовать таблицу соответствия чисел. Пример. Число 10010112 перевести в восьмеричную систему счисления: 001 001 0112 = 1138; 011 001 0012 = 6118 (3 триады); 1 110 011 1012=14358 (4 триады). Перевод чисел из двоичной системы счисления в шестнадцатеричную. Для перевода числа из двоичной системы в шестнадцатеричную его нужно разбить влево и вправо от запятой на тетрады (четверки цифр), начиная с младшего разряда, и каждую такую группу (тетраду) заменить соответствующей шестнадцатеричной цифрой; недостающее число разрядов дополнить нулями. Например:
Пример. Число 10111000112 перевести в шестнадцатеричную систему счисления: 0010111000112 = 2Е316. Перевод чисел из других систем счисления в двоичную Перевод чисел из восьмеричной системы счисления в двоичную. Для перевода восьмеричных чисел в двоичную систему счисления нужно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр). Число необходимо разбить по три разряда и заменить каждую триаду (тройку) соответствующей ей цифрой восьмеричной системы счисления; недостающее число разрядов дополнить нулями. Например:
Пример. Число 5318 перевести в двоичную систему счисления: 5318 = 1010110012; 4758 = 1001111012 = 1001111012; 1428 = 0011000102 = 11000102. Перевод чисел из шестнадцатеричной системы счисления в двоичную. Перевод шестнадцатеричных чисел в двоичную систему аналогичен переводу чисел из восьмеричной системы.
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой (четверкой цифр). Например:
Пример. Число ЕЕ816 перевести в двоичную систему счисления: ЕЕ816 = 1110111010002. Перевод чисел в восьмеричной и шестнадцатеричной системах счисления При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно необходим промежуточный перевод чисел в двоичную систему. Примеры. 1. Число FEA16 перевести в восьмеричную систему счисления: FEA16 = 1111111010102; 1111111010102 = 77528. 2. Число 66358 перевести в шестнадцатеричную систему счисления: 66358 = 1101100111012; 1101100111012 = D9D16. В качестве примера рассмотрим число 4F516. Для перевода в восьмеричную систему сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Для того чтобы преобразовать данное число в двоичное, необходимо каждую цифру представить в виде 4-разрядного двоичного числа: 4F516 = 100 1111 1012. Так как в 1-й и 3-й группах не достает разряда, заполним каждый нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n: (0 ∙ 22 + 1 ∙ 21 + 0 ∙ 20) ∙ (0 ∙ 22 + 1 ∙ 21 + 1 ∙ 20) ∙ (1 ∙ 22 + 1 ∙ 21 + 0 ∙ 20) ∙ (1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20) = 23658. Подтема №9 «Функции алгебры логики и логические элементы» Логика – наука, изучающая законы и формы мышления. Логика изучает внутреннюю структуру процесса мышления, который реализуется в естественно сложившихся формах мышления. Основные формы абстрактного мышления: понятие, суждение (высказывание), умозаключение, доказательство. Алгебра логики (алгебра высказываний) – раздел математической логики, в котором изучают логические операции над высказываниями. Алгебра логики – это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания. Алгебра множеств – одна из основополагающих современных математических теорий, которая позволяет исследовать отношения между множествами и, соответственно, объемами понятий. Между множествами (объемами понятий) могут быть различные виды отношений: ü равнозначность, когда объемы понятий полностью совпадают; ü пересечение, когда объемы понятий частично совпадают; ü подчинение, когда объем одного понятия полностью входит в объем другого, и т. д. Понятие – это форма мышления, в которой отражаются существенные признаки отдельного предмета (или класса однородных предметов), отличающие его от других (например, портфель, трапеция, ураганный ветер). В структуре каждого понятия нужно различать две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков предмета. Для того чтобы раскрыть содержание понятия, следует определить признаки, необходимые и достаточные для выделения данного предмета по отношению к другим предметам. Объем понятия определяется совокупностью предметов, на которую оно распространяется, и может быть представлен в форме множества объектов, состоящего из элементов множества.
Суждение (высказывание) – это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними (например, весна наступила и грачи прилетели). О предметах можно судить верно или неверно, т. е. суждение (высказывание) может быть истинным или ложным. Истинным будет являться суждение, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным суждение будет в том случае, когда связь понятий искажает объективные отношения, не соответствует реальной действительности. Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, предложение «6 – четное число» следует считать высказыванием, так как оно истинное. Предложение «Рим – столица Франции» – тоже высказывание, так как оно ложное. Предложения типа «в городе A более миллиона жителей», «у него голубые глаза» не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называют высказывательными формами. Алгебра логики рассматривает любое высказывание только с одной точки зрения – является оно истинным или ложным. Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если... то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называют логическими связками. Высказывания, образованные из других высказываний с помощью логических связок, называют составными. Высказывания, не являющиеся составными, называют элементарными. Умозаключение – это форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам логического вывода получают новое знание о предметах реального мира (вывод). Умозаключения бывают дедуктивные, индуктивные и по аналогии. В дедуктивных умозаключениях рассуждения ведут от общего к частному. Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» путем умозаключения можно сделать вывод, что: «Ртуть электропроводна». В индуктивных умозаключениях рассуждения ведут от частного к общему.
Например, установив, что отдельные металлы (железо, медь, цинк, алюминий и т. д.) обладают свойством электропроводности, можно сделать вывод, что все металлы электропроводны. Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений. Например, химический состав Солнца и Земли сходный по многим показателям, поэтому, когда на Солнце обнаружили неизвестный на Земле химический элемент гелий, то по аналогии заключили: такой элемент есть и на Земле. Основные операции алгебры логики Отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность – логические операции, необходимые для описания логических высказываний. Алфавит языка логики высказываний, разделен на следующие категории: ü пропозициональные буквы (пропозициональные переменные) – p, q, r, s, t, p1, q1, r1, s1, t1 и т. п.; ü логические знаки (логические союзы); ü технические знаки. Логические и технические знаки приведены в таблице. Элементы алфавита языка логики высказываний
Простые высказывания в алгебре логики обозначают заглавными латинскими буквами: А = {Аристотель – основоположник логики}; В = {На яблонях растут бананы}. Истинному высказыванию ставится в соответствие 1, ложному – 0. Таким образом, А = 1, В = 0. Логическая операция конъюнкции (логическое умножение) Конъюнкция (соединение), или логическое умножение, – логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Операция в естественном языке выражается связкой «и». Обозначается знаком ˄ точкой «·» (в алгебре высказываний – знаком &), в языках программирования имеет обозначение And либо &&, например: А & B; A аnd B; A && B. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т. е. множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам. Высказывание А ∙ В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание «10 делится на 2 и 5 больше 3» истинно, а высказывания «10 делится на 2 и 5 не больше 3», «10 не делится на 2 и 5 больше 3», «10 не делится на 2 и 5 не больше 3» ложны. Логическая операция дизъюнкции (логическое сложение) Дизъюнкция (разделение), или логическое сложение, – логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В обычной речи операция дизъюнкции, выражается связкой «или» и обозначается знаком «˅» (или плюсом), в языках программирования имеет обозначение or, || либо |. Например: A | B; A || B; A or B. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т. е. множеству, получившемуся в результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В. Высказывание А ˅ В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание «10 не делится на 2 или 5 не больше 3» ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3» истинны. Логическая операция инверсии (отрицание) Отрицание (инверсия) – логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. Обозначается чертой над высказыванием Ᾱ либо знаком, например: А. В обычной речи операция выражается словом «не», соответствует словам «неверно, что...», в языках программирования имеет обозначения Not, ~,!, например: ~A;!A; not A. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т. е. множеству, получившемуся в результате отрицания множества А, соответствует множество, дополняющее его до универсального множества. Высказывание Логическая операция импликации (логическое следование) Импликация (тесно связаны) – логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно (обозначение →). В обычной речи операция выражается связками «если... то», «из...следует», «...влечет...». Высказывание А→В ложно тогда и только тогда, когда А истинно, а В ложно. Импликацию можно выразить через дизъюнкцию и отрицание: А→В = Логическая операция эквиваленция (равнозначность), или двойная импликация Эквиваленция (равносильно), или двойная импликация, – логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. В обычной речи операция эквиваленции выражается связками «тогда и только тогда», «в том и только в том случае», «необходимо и достаточно», «...равносильно...». Обозначается знаком ↔ или ~. Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания: «24 делится на 6 тогда и только тогда, когда 24 делится на 3», «23 делится на 6 тогда и только тогда, когда 23 делится на 3» истинны, а высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 5», «21 делится на 6 тогда и только тогда, когда 21 делится на 3» ложны. Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: А↔В = (Ā ˅ В) ∙ (B ˅ А). Логические элементы компьютера Логические элементы – устройства, предназначенные для обработки информации в цифровой форме (последовательность сигналов высокого – 1 и низкого – 0 уровней в двоичной логике, последовательность 0, 1 и 2 в троичной логике, последовательности 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 в десятичной логике). Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными). Всего возможно Будем рассматривать только простейшие и важнейшие логические элементы. Всего возможно Кроме 16 двоичных двухвходовых логических элементов и 256 трехвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трехвходовых троичных логических элементов (троичные функции). Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются такие электронные схемы, как И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер. Работу логических элементов описывают с помощью таблиц истинности. Схема И реализует конъюнкцию двух или более логических значений.
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Если хотя бы на одном входе будет 0, на выходе также будет 0. Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x ˄ y (читается как «x и y»). Операцию конъюнкции на функциональных схемах обозначают знаком &.
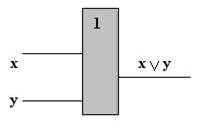
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Если хотя бы на одном входе схемы ИЛИ будет 1, то на ее выходе также будет 1.
Знак «1» на схеме (устаревшее обозначение дизъюнкции) означает, что значение дизъюнкции равно 1, если сумма значений операндов больше или равна 1. Связь между выходом z этой схемы и входами x и y описывают соотношением: z = x ˅ y (читается как «x или y»).
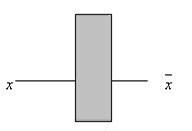
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =
Если на входе схемы 0, то на выходе 1, если на входе 1, то на выходе 0.
Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:
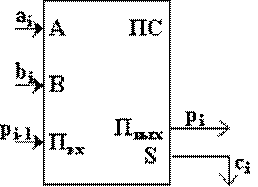
Вентиль представляет собой выполняющий элементарную логическую операцию логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание. Логика работы вентиля основана на битовых операциях с входными цифровыми сигналами в качестве операндов. При создании цифровой схемы вентили соединяют между собой, при этом выход используемого вентиля должен быть подключен к одному или к нескольким входам других вентилей. Сумматоры и триггеры – это относительно сложные устройства, состоящие из более простых элементов – вентилей. Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел. Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров. Условное обозначение и соответствующая таблица истинности:
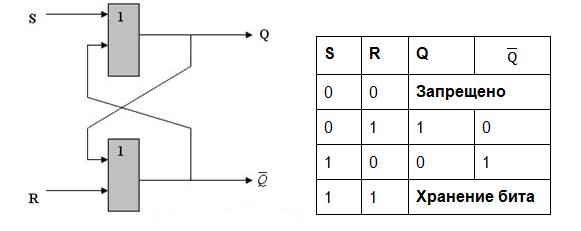
Сложение чисел A и B в одном i-м разряде осуществляется с помощью: ü цифры ai первого слагаемого; ü цифры bi второго слагаемого; ü переноса pi-1 из младшего разряда. В результате сложения получают две цифры: ü цифра ci для суммы; ü перенос pi из данного разряда в старший. Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами. Триггер – это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое – двоичному нулю. Термин «триггер» происходит от английского слова trigger – защелка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip – flop, что в переводе означает «хлопанье». Это звукоподражательное название электронной схемы указывает на ее способность почти мгновенно переходить из одного электрического состояния в другое и наоборот. Самый распространенный тип триггера – так называемый RS – триггер (S и R соответственно от английских слов set – установка и reset – сброс). Он имеет два симметричных входа S и R и два симметричных выхода Q и На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем. Условное обозначение триггера:
На рисунке показаны реализация триггера с помощью вентилей ИЛИ-НЕ и соответствующая таблица истинности.
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ. Если на входы триггера подать S = 1, R = 0, то независимо от состояния на выходе Q верхнего вентиля появится 0. После этого на входах нижнего вентиля окажется R = 0, Q = 0 и выход Q станет равным 1. При подаче 0 на вход S и 1 на вход R на выходе Q появится 0, а на Q – 1. Если на входы R и S подана логическая единица, то состояние Q и Q не меняется. Подача на оба входа R и S логического нуля может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, а для килобайта – соответственно 8
Подтема №10 «Формы логических функций. Функционально-полные системы» Логические формулы С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т. е. заменить логической формулой. Пропозициональная формула – итоговая последовательность знаков алфавита, построенная по определенным правилам и образующая законченное выражение языка логики высказываний. Заглавные латинские буквы A, B и др., которые употребляют в определении формулы, принадлежат языку, используемому для описания самого языка логики высказываний. Буквенные выражения А, (А → В) и др. – это схемы формул. Например, выражение (А ˄ В) есть схема формул (p ˄ q), (p ˄ (r ˅ s)). Определения формулы логики высказываний: ü пропозициональная переменная есть формула; ü если А – произвольная формула, то А – тоже формула; ü если А и В – произвольные формулы, то (А → В), (А ˄ В), (А ↔ В), (А ˅ В) и (А ˅ В) – тоже формулы. Других формул в языке логики высказываний нет. Для формул логики высказываний можно определить понятие интерпретации как приписывание каждой пропозициональной переменной истинностного значения. В качестве примера рассмотрим высказывание: «Если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог». Это высказывание формализуется в виде формулы (A ˅ B) → C. При определенных сочетаниях значений переменных A, B и C она принимает значение «истина», при некоторых других сочетаниях – значение «ложь». Такие формулы называют выполнимыми. Некоторые формулы принимают значение «истина» при любых значениях истинности входящих в них переменных. Например, формула А ˅ Данная формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называют тождественно истинными формулами, или тавтологиями. Высказывания, которые формализуются тавтологиями, называют логически истинными высказываниями. В качестве другого примера рассмотрим формулу Эта формула ложна, так как либо А, либо Такие формулы называют тождественно ложными формулами, или противоречиями. Высказывания, которые формализуются противоречиями, называют логически ложными высказываниями. Если две формулы А и В «одновременно», т. е. при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то их называют равносильными (эквивалентными). Равносильность двух формул алгебры логики обозначают символом «=». Выражения А → В и (А) ˅ В равносильны, а А ˄ В и А ˅ В – нет (значения выражений разные, например, при А = 1, В = 0). Замену формулы другой, ей равносильной, называют равносильным преобразованием данной формулы. Пример. Запишем в форме логического выражения составное высказывание: (2 ∙ 2 = 5 или 2 ∙ 2 = 4) и (2 ∙ 2 ≠ 5 или 2 ∙ 2 ≠ 4). Проанализируем составное высказывание. Оно содержит два простых высказывания: А = 2 ∙ 2 = 5 – ложно (0); В = 2 ∙ 2 = 4 – истинно (1). Перепишем составное высказывание. Получим: (А или В) и (А или В). Необходимо записать высказывание в форме логического выражения. Для этого нужно подставить знаки логических операций (A ˅ B) ˄ (A ˅ B). Выполняем логические операции в строго определенном порядке. Подставим в логическое выражение значения логических переменных и получим значение логической функции F = (A ˅ B) ˄ (A ˅ B) = (0 ˅ 1) ˄ (1 ˅ 0) = 1 ˄ 1 = 1. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т. е. заменить логической формулой. Связь между алгеброй логики и двоичным кодированием Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: 1 и 0. Из этого следует два вывода: 1) одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных; 2) на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. Данные и команды представляются в виде двоичных последовательностей разной структуры и длины. Существуют различные физические способы кодирования двоичной информации. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули, т. е. для кодирования нуля и единицы используют разные уровни напряжения. Основные законы алгебры логики В алгебре логики существует четыре пары основных законов: ü два переместительных (коммутативных); ü два сочетательных (ассоциативных); ü два распределительных (дистрибутивных) ü два закона инверсии. В алгебре логики доказано, что любую логическую функцию можно выразить только через комбинацию логических операций И, ИЛИ и НЕ. Для приведения логических выражений к эквивалентным, но более простым в записи используют ряд логических законов. Закон тождества. Согласно данному закону мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует A = A. Закон противоречия утверждает, что никакое предложение не может быть истинно одновременно со своим отрицанием: «Это яблоко спелое» и «Это яблоко неспелое»
Закон исключенного третьего утверждает, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно, либо ложно; третьего не дано: «Сегодня я либо получу 10, либо не получу». Истинно либо суждение, либо его отрицание A ∨ Закон двойного отрицания заключается в том, что отрицать отрицание какого-нибудь высказывания то же, что утверждать это высказывание: «Неверно, что 2 ∙ 2< >4»
Законы идемпотентности утверждают, что в алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых «сомножителей» равносильна одному из них; дизъюнкция одинаковых «слагаемых» равносильна одному из них: A ∨ A = A; A Законы коммутативности и ассоциативности заключаются в том, что конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел: законы коммутативности: A ∨ B = B ∨ A; A законы ассоциативности: (A ∨ B) ∨ C = A ∨ (B ∨ C); (A Законы дистрибутивности утверждают, что логическое сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции: (A ∨ B) (A Законы де Моргана показывают как отрицаются высказывания: ( ( Данные законы можно выразить в следующих кратких формулировках: · отрицание логического произведения эквивалентно логической сумме отрицаний множителей; · отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.171.20 (0.223 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
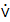
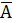 истинно, когда A ложно, и ложно, когда A истинно (например, «Луна — спутник Земли» (А); «Луна — не спутник Земли» (Ᾱ).
истинно, когда A ложно, и ложно, когда A истинно (например, «Луна — спутник Земли» (А); «Луна — не спутник Земли» (Ᾱ).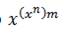 логических функций и соответствующих им логических элементов, где x – основание системы счисления; n – число входов (аргументов); m – число выходов, т. е. бесконечное число логических элементов.
логических функций и соответствующих им логических элементов, где x – основание системы счисления; n – число входов (аргументов); m – число выходов, т. е. бесконечное число логических элементов. двоичных двухвходовых логических элементов и
двоичных двухвходовых логических элементов и 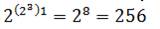 двоичных трехвходовых логических элементов (булева функция).
двоичных трехвходовых логических элементов (булева функция).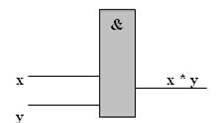
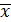 (
(
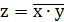 (
(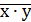 читается как «инверсия x и y»).
читается как «инверсия x и y»).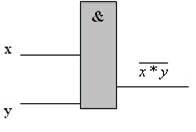
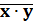
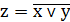 (
(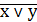 читается как «инверсия x или y»).
читается как «инверсия x или y»).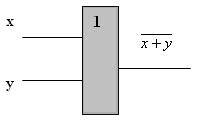
 , причем выходной сигнал Q является логическим отрицанием сигнала
, причем выходной сигнал Q является логическим отрицанием сигнала 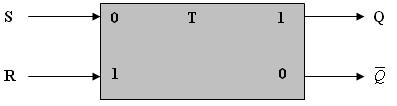
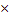 210 = 8192 триггера.
210 = 8192 триггера. , соответствующая высказыванию: «Этот треугольник прямоугольный или косоугольный».
, соответствующая высказыванию: «Этот треугольник прямоугольный или косоугольный».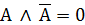 .
.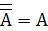 .
.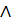 A = A.
A = A.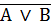 ) =
) = 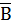 ;
; ) =
) = 


