Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимальные плоские размещения ⇐ ПредыдущаяСтр 8 из 8
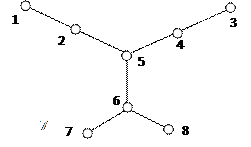
Рассмотрим свойства нумераций j Î F *, соответствующих реализациям дерева t (V, E) каноническими j (vi) < j (vk) < j (vj) < j (vr) или j (vk) < j (vi) < j (vr) < j (vj). (5.2.1.) Не ограничивая общности рассмотрения, полагаем в (5.2.1) j (vi) < j (vj), a j (vk) < j (vr). Класс плоских нумераций пересекается с классом нумераций Ф* (например, монотонная нумерация любой цепи s (V, E)), однако ни один из них не содержится целиком в другом (рис. 5.2.1.).
плоская j Ï F *
неплоская j Î F * Рисунок 5.2.1. Теорема 5.2.1. Нумерация j Î F * вершин дерева t (V, E) является плоской тогда и только тогда, когда соответствующая ей последовательность цепей разложения s j (Vj, Ej),
Доказательство. Необходимость. Покажем, что если нумерация j Î F * является плоской, то условие (5.2.1) выполнено. Предположим, что найдется хотя бы одно Так как j Î F *, то вершины j ( Отсюда, учитывая порядок выделения цепей и сплошность нумерующих последовательностей всех поддеревьев разложения, получаем соотношения j ( Из (5.2.3) и (5.2.4) следует, что при любом соотношении между номерами j (
Достаточность. Пусть нумерация j Î F * вершин дерева t (V, E) удовлетворяет условию теоремы. Разместим вершины Условие (5.2.2) означает, что все нумерации j Î F *, соответствующие каноническим Лемма 5.2.1. Всякая минимальная плоская нумерация j дерева t (V, E) принадлежит классу F *. Доказательство. Разложим дерево t (V, E) на пореберно непересекающиеся цепи s j (Vj, Ej), Если нумерующая последовательность хотя бы одного поддерева разложения, образующегося в процессе выделения цепей s j (Vj, Ej) не является сплошной, то нумерация j не будет плоской, поскольку нумерующая последовательность всего дерева сплошная и каждое поддерево разложения связно. Если хотя бы одна из концевых вершин некоторой цепи s j (Vj, Ej),
Если хотя бы на одной из цепей s j (Vj, Ej), Рассмотрим, какие канонические Теорема 5.2.2. Плоская нумерация j Î F * произвольного дерева t (V, E) является минимальной тогда и только тогда, когда цепи s j (Vj, Ej), Доказательство. Необходимость. Пусть j минимальная плоская нумерация дерева t (V, E). Для вершин 1.Цепь s 1 проходит через вершину vi. При этом из теоремы 5.1.1, леммы 5.1.4 и свойств нумераций класса F * следует, что нумерующие последовательности всех веток к vi будут сплошными. Взаиморасположения их вдоль числовой прямой приведены на рис.5.2.2.
p - четно 1 j (
p – нечетно.
Рисунок 5.2.2. Поскольку минимальная плоская нумерация j дерева t (V, E) принадлежит классу F *, то Из сплошности нумерующих последовательностей всех веток к vi следует возможность перехода на каждой из них к двойственной нумерации. При этом сумму длин всех ребер, инцидентных вершине vi - величину
при p четном
при p нечетном. Необходимым условием минимальности каждого из выражений (5.2.4) и (5.2.5) является, очевидно, выполнение для первой взвешенной суммы соотношений
2.Цепь s 1 не содержит вершину vi. Пусть Достаточность. Нетрудно видеть, что если способ выделения цепей s j (Vj, Ej), Если меняется разложение на цепи s j (Vj, Ej), Поскольку минимальные плоские нумерации содержатся среди рассматриваемых (это следует из необходимости условий теоремы), получаем отсюда минимальность всех нумераций, удовлетворяющих условиям теоремы. ð Алгоритм построения минимальной плоской нумерации
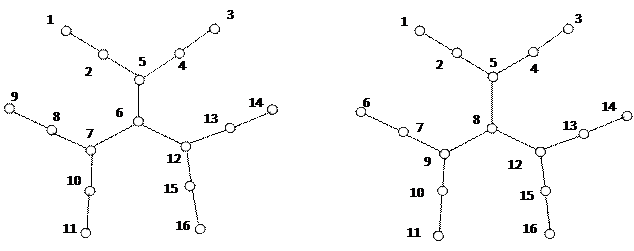
На основе теоремы 5.1.2 можно предложить алгоритм построения минимальной плоской нумерации вершин произвольного дерева. Основу его составляет следующая процедура: 1. Выбрать в текущем поддереве разложения (исходном дереве) произвольную вершину дерева v 0. 2. Перейти от вершины v 0 по веткам с наибольшим числом вершин в некоторую висячую вершину v 1. 3. Начиная от вершины v 1, построить по веткам с наибольшим числом вершин цепь в некоторую другую висячую вершину v 2. 4. Присвоить вершинам v 1 и v 2 наибольшие и наименьшие номера из диапазона, выделенного под текущее поддерево разложения (1 и n для исходного дерева). 5. Занумеровать монотонно цепь, соединяющую вершины v 1 и v 2, оставляя под каждое выделяемое поддерево разложения соответствующие диапазоны номеров. Процедура повторяется до тех пор, пока не будут занумерованы все вершины. Пример 5.2.1. Для нижеприведенного дерева одна из возможных минимальных плоских нумераций имеет следующий вид:
Для реализации алгоритма необходимо предварительно вычислить веса веток ко всем вершинам дерева и упорядочить их. Для произвольного n – вершинного дерева это можно сделать с линейной трудоемкостью O (n), используя дополнительную память объема O (n log n) [12]. Для небольших деревьев с n £ 15 минимум функционала (5.1.1) в классе плоских нумераций совпадает с глобальным минимумом в классе всех нумераций. Для больших значений n минимум в классе плоских нумераций в общем случае не позволяет достичь глобального минимума, достигаемого на нумерациях, которым соответствуют реализации деревьев Пример 5.2.2. Для следующего дерева t (V, E) с числом вершин n =16 минимальная нумерация не является плоской.
минимальная плоская нумерация j минимальная нумерация j Оценки длин деревьев Алгоритм построения минимальной нумерации произвольного дерева имеет сложную рекурсивную структуру с трудоемкостью Каково значение самого минимума, насколько оно отличается, например, от среднего значения функционала (5.1.1) на множестве всех n! нумераций. Оценим минимум сверху через максимальное значение функционала (5.1.1) на множестве всех n – вершинных деревьев при использовании нумераций j Î F *. Геометрическая интерпретация нумераций класса F * Рассмотрим линейную укладку дерева t (V, E), | V |= n соответствующую произвольной нумерации j Î F *. Для этого разместим вершины дерева вдоль числовой прямой таким образом, чтобы каждая вершина
... ...... 1 Рисунок 5.3.1 Разобьем множество всех дуг на ярусы. К первому ярусу отнесем внешнюю дугу, соединяющую, очевидно, точки с координатами 1 и n и соответствующую цепи s 1 (V 1 , E 1). Ко второму ярусу отнесем дуги, которые становятся внешними после удаления дуги первого яруса. Они соответствуют цепям, выделяемым в поддеревьях, образующихся после выделения цепи s 1 (V 1 , E 1) и т.д. Обозначим через q - общее число ярусов, ni -число цепей i -го яруса, Теорема 5.3.1. Для любого дерева t (V, E), | V |= n и нумерации j Î F *
Доказательство. Поскольку цепи s j (Vj, Ej),
Так как нумерация j на каждой цепи Учитывая, что ni ³ 1,
при n нечетном,
при n четном. Таким образом, утверждение теоремы справедливо при любом n. ð Подсчитаем среднее значение минимизируемого функционала (5.1.1) для произвольного графа G (V, E), / V /= n на множестве всех n! нумераций - величинуравную
При последовательном построении n! нумераций на концах любого ребра e Î E каждая пара номеров
Поскольку это верно для произвольного ребра e Î E, то числитель в (5.3.3) равен Так как в дереве t (V, E), | V |= n число ребер | E |= n -1, то среднее значение длины дерева на множестве всех нумераций равно (n 2 -1)/3. Учитывая утверждение теоремы 5.3.1, получаем, что при Список литературы 1. Мельников О.И. Занимательные задачи по теории графов. - Минск: НТ ООО "ТетраСистемс", 2001. - 144 с. 2. Лекции по теории графов / Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. - М.: Наука, 1990. - 384 с. 3. Мальцев И.А.Дискретная математика. - СПб.: Изд-во «Лань», 2011. - 304 с. 4. Перечисление графов / Харари Ф., Палмер Э. – М.: Изд-во «Мир», 1977. – 324 с. 5. Иорданский М.А. Конструктивные описания графов // Дискретный анализ и исследование операций. - 1996. - Т. 3, № 4. - С. 35 - 63. 6. Бурков Е.В. Операционные базисы замкнутых классов графов // Материалы IX международного семинара "Дискретная математика и её приложения" (Москва, 18-23 июня 2007г.). - М.: Изд-во мехмата МГУ. 2007. - С. 105-116. 7. Иорданский М.А. Конструктивная классификация графов // Моделирование и анализ информационных систем. - 2012. - Т. 19, № 4. - С. 144 - 153. 8. Alon N. Tough Ramsey Graphs Without Short Cycles // Journal of Algebraic Combinatorics. – 1995. – V.4, № 3. – P.189 - 195. 9. Бурков Е.В. Конструктивные описания планарных и эйлеровых графов // Вестник Нижегородского государственного университета. Математика. - 2010. № 5(1). - С. 165 - 170. 10. Иорданский М.А. Конструктивные описания гамильтоновых графов // Вестник Нижегородского государственного университета. Математика. - 2012.,№ 3(1). - С. 137 - 140. 11. Иорданский М.А. Избыточность конструктивных описаний гамильтоновых планарных графов // Материалы XI Международного семинара «Дискретная математика и её приложения» (Москва, МГУ, 18-22 июня 2012 г.) – М: Изд-во механико-математического факультета МГУ. 2012. - С. 285-288. 12. Иорданский М.А Минимальные плоские размещения деревьев // Методы дискретного анализа в решении экстремальных задач. - 1979. выпуск 33. - С. 3 - 30. 13. Chung F.R.K. On optimal linear arrangement algorithm for undirected trees // SIAM J. Comput.- 1984. -V. 8, № 1. - P. 15 - 32.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.36.141 (0.112 с.) |
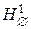 - суперпозициями над S. Линейная укладка дерева t (V, E) называется плоской, если она допускает геометрическую реализацию графа в полуплоскости. Соответствующая ей нумерация j также называется плоской. Нумерация j является плоской тогда и только тогда, когда между номерами вершин произвольной пары ребер (v, vj) и (vk, vr) не существует соотношений:
- суперпозициями над S. Линейная укладка дерева t (V, E) называется плоской, если она допускает геометрическую реализацию графа в полуплоскости. Соответствующая ей нумерация j также называется плоской. Нумерация j является плоской тогда и только тогда, когда между номерами вершин произвольной пары ребер (v, vj) и (vk, vr) не существует соотношений:
 обладает следующим свойством
обладает следующим свойством связно при
связно при 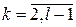 (5.2.2)
(5.2.2)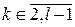 такое, что
такое, что  не имеет общей вершины с цепью s k. Выделим в дереве цепь, соединяющую вершину
не имеет общей вершины с цепью s k. Выделим в дереве цепь, соединяющую вершину 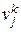 цепи s k с вершиной
цепи s k с вершиной 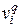 из
из  sqÎ
sqÎ 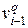 и
и 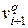 (
( и
и 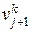 )вершины, смежные с
)вершины, смежные с 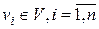 вдоль целочисленной прямой в точках с координатами j (
вдоль целочисленной прямой в точках с координатами j ( 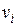 ) и соединим дугами смежные вершины. Дуги, соответствующие ребрам одной цепи, очевидно, не пересекаются, так как нумерация вдоль каждой цепи s j,
) и соединим дугами смежные вершины. Дуги, соответствующие ребрам одной цепи, очевидно, не пересекаются, так как нумерация вдоль каждой цепи s j, 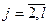 содержится номер лишь одной вершины
содержится номер лишь одной вершины 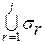 , вершина
, вершина 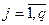 , соединяющие в каждом поддереве разложения вершины с наименьшими и наибольшими номерами. Покажем, что если j минимальная плоская нумерация, то указанное разложение обладает всеми свойствами нумераций из класса Ф* и, следовательно q = l.
, соединяющие в каждом поддереве разложения вершины с наименьшими и наибольшими номерами. Покажем, что если j минимальная плоская нумерация, то указанное разложение обладает всеми свойствами нумераций из класса Ф* и, следовательно q = l. не является висячей в поддерева, в котором она выделяется, то, не выходя из класса плоских нумераций, можно уменьшить значение функционала (5.1.1), перейдя к двойственной нумерации на поддереве, "висящем" на такой концевой вершине.
не является висячей в поддерева, в котором она выделяется, то, не выходя из класса плоских нумераций, можно уменьшить значение функционала (5.1.1), перейдя к двойственной нумерации на поддереве, "висящем" на такой концевой вершине. - суперпозиции надS соответствуют минимальным плоским нумерациям. Выделим в дереве t { V, E) произвольную вершину
- суперпозиции надS соответствуют минимальным плоским нумерациям. Выделим в дереве t { V, E) произвольную вершину  степени s (vi)= p и все инцидентные ей ребра (vi, vr),
степени s (vi)= p и все инцидентные ей ребра (vi, vr),  . Любая вершина vq ¹ vi связана с вершиной vi единственной цепью. Будем говорить, что вершина vq принадлежит ветке, выходящей из вершины vi по ребру (vi, vr),
. Любая вершина vq ¹ vi связана с вершиной vi единственной цепью. Будем говорить, что вершина vq принадлежит ветке, выходящей из вершины vi по ребру (vi, vr),  , если в vq можно попасть из vi по цепи, содержащей ребро (vi, vr). Число вершин ветки определяет её вес.
, если в vq можно попасть из vi по цепи, содержащей ребро (vi, vr). Число вершин ветки определяет её вес.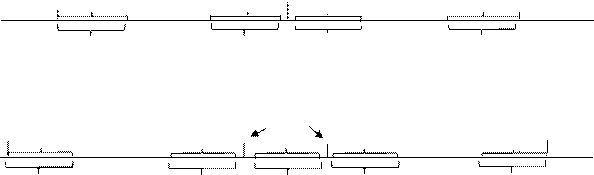 1 j (
1 j (  ) · · · j (
) · · · j ( 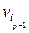 ) j (vi) j (
) j (vi) j ( 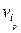 ) · · · j (
) · · · j ( 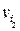 ) n
) n
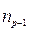

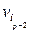 ) j (vi) j (
) j (vi) j (  и
и 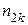 ,
, 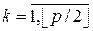 - число вершин в ветках, по которым k -ая цепь разложения проходит через вершину vi. При нечетном p указаны две возможности для нумерации вершины vi, поскольку последняя цепь разложения проходит через vi только по одной ветке (с числом вершин пр) и в зависимости от выбора направления нумерации на этой цепи последняя ветка может быть занумерована как до, так и после вершины vi (в последующих расчетах выбран вариант, когда последняя ветка занумерована до вершины vi).
- число вершин в ветках, по которым k -ая цепь разложения проходит через вершину vi. При нечетном p указаны две возможности для нумерации вершины vi, поскольку последняя цепь разложения проходит через vi только по одной ветке (с числом вершин пр) и в зависимости от выбора направления нумерации на этой цепи последняя ветка может быть занумерована как до, так и после вершины vi (в последующих расчетах выбран вариант, когда последняя ветка занумерована до вершины vi).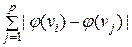 , можно оценить сверху следующим образом:
, можно оценить сверху следующим образом: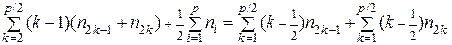 (5.2.4)
(5.2.4)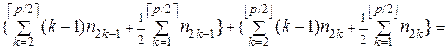
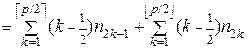 (5.2.5)
(5.2.5)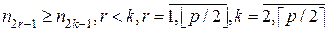 , а для второй взвешенной суммы соотношений
, а для второй взвешенной суммы соотношений 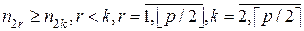 . В противном случае, поменяв порядок нумерации вершин соответствующих веток, можно уменьшить величину
. В противном случае, поменяв порядок нумерации вершин соответствующих веток, можно уменьшить величину  проходят через вершины vi по веткам с наибольшим числом вершин.
проходят через вершины vi по веткам с наибольшим числом вершин.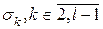 - первая цепь разложения, проходящая через vi. Так как
- первая цепь разложения, проходящая через vi. Так как 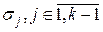 . Число вершин в этой ветке больше, чем в какой-либо другой ветке к vi, так как она содержит цепь s 1, проходящую через вершины дерева по веткам с наибольшим числом вершин. Следовательно, нарушение условий теоремы невозможно ни на какой паре веток к vi, одна из которых содержит цепь s 1. Поскольку нумерация остальных веток к vi производится сплошными нумерующими последовательностями, то дальнейшее доказательство проводится аналогично первому случаю. Итак, и для всех вершин vi, через которые не проходит цепь s 1,условия теоремы также выполнены, то есть все цепи разложения s j (Vj, Ej),
. Число вершин в этой ветке больше, чем в какой-либо другой ветке к vi, так как она содержит цепь s 1, проходящую через вершины дерева по веткам с наибольшим числом вершин. Следовательно, нарушение условий теоремы невозможно ни на какой паре веток к vi, одна из которых содержит цепь s 1. Поскольку нумерация остальных веток к vi производится сплошными нумерующими последовательностями, то дальнейшее доказательство проводится аналогично первому случаю. Итак, и для всех вершин vi, через которые не проходит цепь s 1,условия теоремы также выполнены, то есть все цепи разложения s j (Vj, Ej), 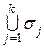 ,
, 
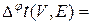 26
26 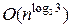 [13]. Относительно простой алгоритм построения минимальной плоской нумерации можно рассматривать как способ приближенного решения задачи построения минимальной нумерации. В работе [12] показано, что минимум в классе плоских нумераций может превосходить глобальный минимум не более чем в полтора раза.
[13]. Относительно простой алгоритм построения минимальной плоской нумерации можно рассматривать как способ приближенного решения задачи построения минимальной нумерации. В работе [12] показано, что минимум в классе плоских нумераций может превосходить глобальный минимум не более чем в полтора раза.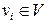 попала в точку с координатой
попала в точку с координатой 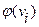 . Выделим вершины, являющиеся концевыми для цепей разложения s j (Vj, Ej),
. Выделим вершины, являющиеся концевыми для цепей разложения s j (Vj, Ej),  и
и 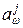 . Каждой цепи s j (Vj, Ej),
. Каждой цепи s j (Vj, Ej), 
 - цепь, соответствующая k -ой дуге i -го яруса.
- цепь, соответствующая k -ой дуге i -го яруса. ë n 2 /4 û
ë n 2 /4 û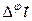 так
так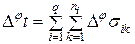 . (5.3.1)
. (5.3.1)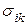 монотонна, то величина
монотонна, то величина 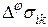 равна длине отрезка [
равна длине отрезка [  ,
, 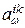 ]. Отрезки, соответствующие цепям одного яруса, очевидно, не имеют общих точек. Тогда, учитывал способ разбиения цепей на ярусы, получаем
]. Отрезки, соответствующие цепям одного яруса, очевидно, не имеют общих точек. Тогда, учитывал способ разбиения цепей на ярусы, получаем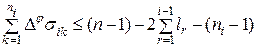 . (5.3.2)
. (5.3.2)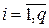 , q £ ë n /2 û, из (5.3.1) и (5.3.2) следует
, q £ ë n /2 û, из (5.3.1) и (5.3.2) следует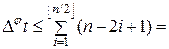 n ë n/2 û - ë n/2 û é n/2 ù + ë n/2 û =ë n/2 û é n/2 ù = ë n2/4 û
n ë n/2 û - ë n/2 û é n/2 ù + ë n/2 û =ë n/2 û é n/2 ù = ë n2/4 û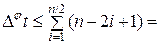 n (n/2)- (n/2) (n/2+1) + n/2= n/2(n/2-1)+ n/2=n2/4
n (n/2)- (n/2) (n/2+1) + n/2= n/2(n/2-1)+ n/2=n2/4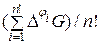 (5.3.3)
(5.3.3) побывает 2(n -2)! раз. Длина ребра e принимает при этом значения | i - j | равные
побывает 2(n -2)! раз. Длина ребра e принимает при этом значения | i - j | равные 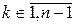 по (n - k) раз. Общий вклад ребра e в числитель выражения (5.3.3) равен
по (n - k) раз. Общий вклад ребра e в числитель выражения (5.3.3) равен .
. и среднее значение длины графа G на множестве всех n! нумераций равно
и среднее значение длины графа G на множестве всех n! нумераций равно 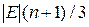 .
.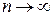 значение минимизируемого функционала 5.1.1 на множестве нумераций из класса F *, по крайней мере, на четверть меньше среднего значения на множестве всех нумераций. При использовании минимальных нумераций или минимальных плоских нумераций сокращение длины дереваможет быть еще значительнее.
значение минимизируемого функционала 5.1.1 на множестве нумераций из класса F *, по крайней мере, на четверть меньше среднего значения на множестве всех нумераций. При использовании минимальных нумераций или минимальных плоских нумераций сокращение длины дереваможет быть еще значительнее.