
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классы всех графов, мультиграфов и простых графовСодержание книги Поиск на нашем сайте Рассмотрим конструктивные описания некоторых замкнутых и Теорема 4.2.1. Замкнутый класс всех графов имеет элементный базис Доказательство. Из определения операций склейки следует, что каждая из них сохраняет отсутствие в графах-операндах изолированных вершин, петель и ребер. Таким образом, имеем 1. Построим пустой граф, содержащий | V (G)| вершин. Это можно сделать с помощью (| V (G)|-1) операцийсклейки по O 0 . Вначале реализуется граф 2. Дополним пустой граф ребрами и (или) петлями до величины равной | E (G)| с помощью операций склейки заданных пар вершин текущего графа с K 2 по O 2 и (или) заданных вершин текущего графа с C 1 по O 1. После выполнения всех указанных операций склейки получаем требуемый граф G (V, E). При этом установлена полнота системы операций склейки. Покажем минимальность по включению этой системы. Без операций склейки по O 0 нельзя реализовать несвязные графы, поскольку все графы элементного базиса связны. Без операций склейки по O 1 нельзя построить графы, вершины которых инцидентны нескольким петлям. Без операций склейки по O 2 нельзя построить графы, содержащие кратные ребра. ð На основе подмножеств порождающих базисов замкнутого класса всех графов можно строить конструктивные описания для различных подклассов всех графов. В [7] построена решетка всех 35 таких нетривиальных замкнутых подклассов. Ниже приведены конструктивные описания некоторых из них Графы, не содержащие петель, называются мультиграфами. Следствие 4.2.1. Замкнутый класс мультиграфов имеет элементный базис Любая операция склейки по подграфу, содержащему не более одной вершины, очевидно, сохраняет отсутствие циклов. Граф, не содержащий циклы, образует лес. Следствие 4.2.2. Замкнутый класс лесов имеет элементный базис Следствие 4.2.3. Замкнутый класс деревьев имеет элементный базис Для сохранения отсутствия в графах кратных ребер в общем случае необходимо накладывать ограничение на выбор в графах-операндах отождествляемых подграфов, содержащих не менее двух вершин (см. рис. 4.1.2). Достаточным условием для этого может быть следующее ограничение: каждой паре несмежных в подграфе Следствие 4.2.4. Класс простых графов Подграф G ’ Í G называется порожденным, если для каждой пары смежных вершин, включаемых в G ’, в подграф включается и соответствующее ребро. Подграф, порожденный вершинами V ’ Í V (G), обозначается через G (V ’). Число вершин связного графа G, удаление которых приводит к несвязному или одновершинному графу, называется числом вершинной связности (связностью), обозначаемым через À (G). Подмножество V ’ Í V (G) называется разделяющим множеством вершин графа G, если граф G (V \ V ’) имеет больше компонент связности, чем граф G. Если | V (G)|> max { | V (G 1)|,| V (G 2)| }, то V ( Теорема 4.2.2. < H > - замкнутый класс простых графов имеет счетные элементный и операционный базисы. Доказательство. Бесконечность элементного базиса следует из того, что каждый полный граф Kn, n ³ 3 не может быть получен в результате выполнения нетривиальной операции < H > - склейки. Поскольку в противном случае множество V ( Покажем бесконечность операционного базиса. Рассмотрим счетную последовательность графов À (G)< n -1. Следовательно, в операционный базис должно входить счетное множество операций < H > - склейки по Kn, n =1,2,…. ð Следствие 4.2.5. Мощность множества всех < H > – замкнутых классов простых графов континуальна. 4.3. Классы планарных графов Выделим в плоском графе G некоторую грань Г, имеющую связную границу. Перечисление без повторения всех вершин грани Г последовательно вдоль границы грани назовем круговым обходом грани Г. Окружность, все точки которой принадлежат грани Г или её границе, называется вписанной в грань Г. Каждый планарный граф G допускает плоскую укладку, в которой все вершины произвольной грани Г со связной границей расположены на окружности, вписанной в грань Г. Пусть все вершины подграфов Теорема 4.3.1. Операции H Ä – склейки сохраняют планарность графов. Доказательство. Рассмотрим плоские укладки графов G 1 и G 2, в которых все вершины соответственно граней Г1 и Г2 расположены вдоль вписанных в них окружностей. Каждую из этих окружностей можно интерпретировать как линию разреза сферы на две полусферы, на которых размещены рассматриваемые плоские укладки графов G 1 и G 2. Для отождествления вершин из Конструктивные описания планарных графов с использованием различных модификаций операции Теорема 4.3.2. Класс планарных графов H Ä -замкнут с порождающими базисами Доказательство. Планарность графа G, реализуемого H Ä -суперпозицией над Реализуемость любого планарного графа G указаннойсуперпозицией устанавливается с помощью построений аналогичных тем, что использовались при доказательстве теоремы 4.2.1. В данном случае при заполнении ребрами пустого графа они соединяют вершины, принадлежащие границе одной грани в плоской укладке текущего графа. Минимальность по включению множеств Переходя к подмножествам порождающих базисов H Ä -замкнутого класса планарных графов, а, также накладывая дополнительные ограничения на допустимые операции H Ä -склейки, можно получать различные замкнутые подклассы планарных графов. Если | V ( Следствие 4.3.1. Класс планарных графов H Г - замкнут с порождающими базисами Следствие 4.3.2. Класс планарных мультиграфов H Г - замкнут с порождающими базисами Следствие 4.3.3. Класс простых планарных графов Если ограничиться использованием операций Теорема 4.3.3. Доказательство. Поскольку все графы из элементного базиса Be являются простыми планарными и операции Покажем, что каждый простой планарный граф G может быть реализован Если G - полный граф, то он может содержать не более 4 вершин (K 5 не является планарным). Если граф G не является связным, то достаточно построить все его компоненты связности, объединив их затем с помощью операций склейки по O 0. Если простой связный планарный граф G содержит разделяющую вершину vi, то в G можновыделить два подграфа, объединение которых совпадает с G, а пересечение – с вершиной vi. Если взять в качестве графов - операндов графы G 1 и G 2, изоморфные этим подграфам, то получаем описание Если простой связный планарный граф G не содержит разделяющих вершин, то выберем в G вершину vi, смежную не со всеми вершинами (такая вершина найдется, так как граф G не является полным). Обозначим через Vi множество вершин, смежных с вершиной vi. Выделим в графе G связные подграфы Так как G 1 и G 2 являются простыми связными планарными графами и содержат меньшее число вершин, чем граф G, то, последовательно применяя к ним все предыдущие рассуждения в итоге, придем к системе полных графов из Be. Рассматривая этот процесс в обратном направлении, получаем задание произвольного простого планарного графа G в виде Минимальность по включению множества графов из Be следует из того, что ни один из них нельзя получить, используя операции Минимальность по включению множества графов из Переход от операций
O0 O1 O2 O3 O4 O5
Рисунок 4.3.1 Если накладывать на операции склейки более жесткие ограничения, требуя, на пример, чтобы отождествляемые подграфы были порожденными, то для построения простых планарных графов потребуется ещё большее разнообразие типов операций склейки. При использовании операций склейки по порожденным подграфам увеличивается избыточность конструктивных описаний. Для ограничения величины избыточности рассматривают процессы сборки простых планарных графов, когда вершины из Эйлеровы графы Граф G является эйлеровым тогда и только тогда, когда степени всех его вершин четны (теорема 1.3.1). Выясним, при каких ограничениях на операции склейки они сохраняют свойство эйлеровости графов-операндов. Теорема 4.4.1. Если графы G 1 и G 2 эйлеровы, то граф G = Доказательство. Рассмотрим любую вершину где Необходимость. Если графы G 1 и G 2 являются эйлеровыми, то степени Достаточность. Если степени вершин отождествляемых подграфов Следствие 4.4.1. Операции H Æ - склейки сохраняют эйлеровость графов. Использование операций H Æ - склейки по пустым подграфам упрощает конструктивное описание, минимизируя избыточность задания. Теорема 4.4.2. Класс эйлеровых графов H Æ - замкнут с порождающими базисами Доказательство. Каждый эйлеров граф G может быть разложен на пореберно непересекающиеся простые циклы (следствие 1.3.1).Бесконечность элементного базиса следует из того, что простые циклы С n, n =1,2,… не содержат эйлеровых подграфов и поэтому все они входят в Be. Бесконечность операционного базиса следует из того, что для любого сколь угодно большого n найдется эйлеров граф G, | V (G)|= n, связность которого À (G)> n и обхват g (G) (длина кратчайшего простого цикла) удовлетворяет условию g (G) > n [8]. Покажем, что такой граф не может быть получен склейкой по Ok, k £ n. Если V ( Следствие 4.4.2. Класс обыкновенных эйлеровых графов Далее ограничимся рассмотрением эйлеровых планарных графов. При этом операционный базис станет конечным и возможно использование различных базисов. В работе [9] были получены следующие результаты. Лемма 4.4.1. В каждом эйлеровом планарном графе найдется простой цикл, содержащий не более трех вершин степени больше двух. Доказательство. Не ограничивая общности рассмотрения можно считать граф простым и не содержащим вершин степени два. Действительно, если перейти к топологически эквивалентному (не содержащему вершин второй степени) графу, то из существования в нем требуемого цикла будет следовать существование его и в исходном графе. При наличии в графе петель или кратных ребер утверждение леммы очевидно. Пусть G произвольный простой эйлеров планарный граф, не содержащий вершин степени два. Так как в эйлеровом графе не может быть вершин нечетной степени, то степени всех вершин графа G не меньше четырех. В любом графе G, | V (G)|= n имеет место равенство Предположим, что утверждение леммы неверно для графа G, то есть все простые циклы графа G имеют длину не меньше 4. Рассмотрим произвольную плоскую укладку графа G. Для величины Q (G), равной общему числу рёбер вокруг всех граней графа G, получаем оценки 2 m = Q (G) ³ 4 f, откуда следует, что m ³ 2 f. Учитывая равенство (2.2.1), получаем утверждение m £ 2 n -4, противоречащее соотношению (4.4.2). ð Операции склейки, сохраняющие эйлеровость и планарность графов, обозначим как операции Теорема 4.4.3. Класс эйлеровых планарных графов Доказательство. Поскольку простые циклы С n, n =1,2,… являются эйлеровыми и планарными, то обоснование 1. M =1. Таким графом является простой цикл 2. Предположим, что все эйлеровы планарные графы с числом ребер 3. Пусть G произвольный эйлеров планарный граф, содержащий m +1 ребер. Если G является простым циклом, то G Î Покажем минимальность по включению используемых типов операций Рассмотренный операционный базис не является единственным для класса эйлеровых планарных графов. Справедлива Теорема 4.4.4. Класс эйлеровых планарных графов Доказательство этой теоремы, требующее более тщательного анализа структуры эйлеровых планарных графов, приведено в [9]. ð Различные операционные базисы можно выделить и для некоторых других замкнутых классов графов. Гамильтоновы графы В гамильтоновом графе G можно выделить цепь, содержащую все вершины графа, называемую гамильтоновой цепью графа G. Сформулируем условия наследования свойства гамильтоновости при выполнении операций склейки.
Лемма 4.5.1. Граф G = Доказательство. Действительно, в первом случае гамильтонов цикл результирующего графа соответствует гамильтонову циклу графа-операнда, обладающего не меньшим числом вершин. Во втором случае гамильтонов цикл результирующего графа соответствует объединению гамильтоновых цепей графов-операндов, не содержащих ребра, отождествляемого при выполнении операции склейки. ð Операции, удовлетворяющие указанным ограничениям, обозначим как операции Теорема 4.5.1. Конструктивные описания Доказательство. Поскольку все графы элементного базиса Покажем, что при этом можно получить любой гамильтонов граф Далее, не теряя общности рассуждений, ограничимся рассмотрением простых гамильтоновых графов Покажем, что использования операций 1. Подграфы склейки
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.015 с.) |

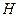 - замкнутых классов графов. Множество всех графов Â является, очевидно, замкнутым классом. В работе [5] были получены следующие конструктивные описания вышеназванных классов.
- замкнутых классов графов. Множество всех графов Â является, очевидно, замкнутым классом. В работе [5] были получены следующие конструктивные описания вышеназванных классов.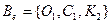 и операционный базис
и операционный базис 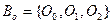 .
.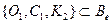 . Поскольку элементный базис единственный, то для доказательства обратного включения достаточно показать, что любой граф G (V, E) представим в виде суперпозиции графов из множества
. Поскольку элементный базис единственный, то для доказательства обратного включения достаточно показать, что любой граф G (V, E) представим в виде суперпозиции графов из множества 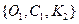 . Рассмотрим следующую суперпозицию.
. Рассмотрим следующую суперпозицию.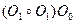 , состоящий из двух изолированных вершин, а затем с помощью операций склейки текущего графа с O 1 по O 0 число изолированных вершин доводится до | V (G)|.
, состоящий из двух изолированных вершин, а затем с помощью операций склейки текущего графа с O 1 по O 0 число изолированных вершин доводится до | V (G)|.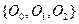 трех типов
трех типов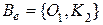 и операционный базис
и операционный базис 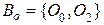 .
.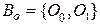 .
.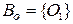 .
.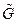 вершин должна соответствовать пара несмежных вершин хотя бы в одном из графов-операндов
вершин должна соответствовать пара несмежных вершин хотя бы в одном из графов-операндов 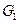 или
или 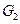 . Соответствующую систему ограничений на операции склейки обозначим через
. Соответствующую систему ограничений на операции склейки обозначим через 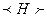 . При этом из теоремы 4.2.1 получаем
. При этом из теоремы 4.2.1 получаем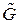 ) является разделяющим множеством вершин связного графа G =
) является разделяющим множеством вершин связного графа G = 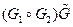 . Указанное неравенство имеет место при выполнении любой нетривиальной операции склейки по порожденному подграфу (операции < H > - склейки). Введенное ограничение на операции склейки существенно уменьшает «силу» операций, что приводит к увеличению мощности порождающих базисов.
. Указанное неравенство имеет место при выполнении любой нетривиальной операции склейки по порожденному подграфу (операции < H > - склейки). Введенное ограничение на операции склейки существенно уменьшает «силу» операций, что приводит к увеличению мощности порождающих базисов.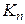 ) £ n -2, но по определению связность полного графа À (
) £ n -2, но по определению связность полного графа À ( 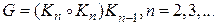 . Каждый граф G этой последовательности имеет связность À (G)= n -1 и поэтому G не может быть получен в результате выполнения склейки
. Каждый граф G этой последовательности имеет связность À (G)= n -1 и поэтому G не может быть получен в результате выполнения склейки 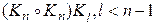 , так как при этом
, так как при этом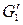 и
и 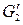 принадлежат граням со связными границами Г1 и Г2 соответственно в графах G 1 и G 2. Преобразуем плоские укладки графов G 1 и G 2 таким образом, чтобы все вершины этих граней располагались вдоль окружностей, вписанных соответственно в грани Г1 и Г2. Отождествим подграфы
принадлежат граням со связными границами Г1 и Г2 соответственно в графах G 1 и G 2. Преобразуем плоские укладки графов G 1 и G 2 таким образом, чтобы все вершины этих граней располагались вдоль окружностей, вписанных соответственно в грани Г1 и Г2. Отождествим подграфы  H Ä - склейки.
H Ä - склейки.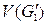 с вершинами из
с вершинами из 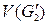 в соответствии с круговыми обходами граней Г1 и Г2 достаточно поворота одной полусферы относительно другой вдоль линии разреза с «растяжениями» или «сжатиями» в случае необходимости длин дуг окружностей, соединяющих вершины из
в соответствии с круговыми обходами граней Г1 и Г2 достаточно поворота одной полусферы относительно другой вдоль линии разреза с «растяжениями» или «сжатиями» в случае необходимости длин дуг окружностей, соединяющих вершины из 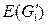 с ребрами из
с ребрами из 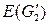 новые ребра не появляются, то результирующий граф G планарен. ð
новые ребра не появляются, то результирующий граф G планарен. ð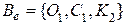 и
и  .
.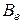 и
и 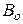 устанавливается также как и при доказательстве теоремы 4.2.1. ð
устанавливается также как и при доказательстве теоремы 4.2.1. ð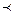 H Г
H Г 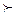 -замкнут с порождающими базисами
-замкнут с порождающими базисами 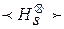 - склейки), то есть
- склейки), то есть 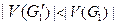 и
и 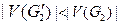 , то получаем следующий результат.
, то получаем следующий результат.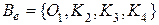 и
и 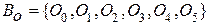 .
.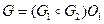 , в котором, очевидно, используется операция
, в котором, очевидно, используется операция 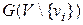 и звезду с центром в вершине vi и с множеством висячих вершин Vi. Если выбрать графы-операнды G 1 и G 2 изоморфными соответственно этим подграфам, то получаем для графа G представление
и звезду с центром в вершине vi и с множеством висячих вершин Vi. Если выбрать графы-операнды G 1 и G 2 изоморфными соответственно этим подграфам, то получаем для графа G представление 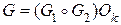 , k = | Vi |. При этом используется операция
, k = | Vi |. При этом используется операция 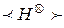 - склейки к операциям
- склейки к операциям 
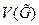 образуют минимальное разделяющее множество вершин результирующего графа каждой операции склейки. При использовании таких операций склейки число необходимых типов операций склейки – мощность операционного базиса, увеличивается до 16. Если же потребовать, чтобы и число ребер в подграфах склейки было минимальным, то мощность операционного базиса становится равной 22 [5]. Элементный базис при этом остается неизменным и содержит полные графы.
образуют минимальное разделяющее множество вершин результирующего графа каждой операции склейки. При использовании таких операций склейки число необходимых типов операций склейки – мощность операционного базиса, увеличивается до 16. Если же потребовать, чтобы и число ребер в подграфах склейки было минимальным, то мощность операционного базиса становится равной 22 [5]. Элементный базис при этом остается неизменным и содержит полные графы.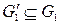 и
и 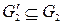 четны.
четны.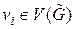 . Каждая из них является результатом отождествления вершин
. Каждая из них является результатом отождествления вершин 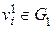 и
и 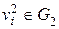 . Из определения операции склейки следует, что
. Из определения операции склейки следует, что 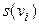 - степень вершины
- степень вершины 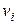 в графе G можно подсчитать по формуле
в графе G можно подсчитать по формуле 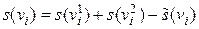 , (4.4.1)
, (4.4.1)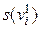 - степень вершины
- степень вершины 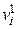 в графе G 1;
в графе G 1; 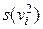 - степень вершины
- степень вершины 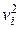 в графе G 2;
в графе G 2; 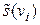 - степень вершины
- степень вершины 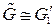 и
и 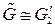 , то степени всех вершин отождествляемых подграфов четны.
, то степени всех вершин отождествляемых подграфов четны.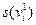 и
и 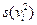 . Отсюда, учитывая (4.4.1), получаем четность степеней
. Отсюда, учитывая (4.4.1), получаем четность степеней 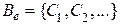 и
и 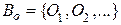 .
.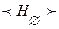 - замкнут с порождающими базисами
- замкнут с порождающими базисами 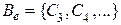 и
и 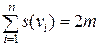 . Поскольку в рассматриваемом графе G степень каждой вершины не меньше 4, то справедливо соотношение
. Поскольку в рассматриваемом графе G степень каждой вершины не меньше 4, то справедливо соотношение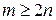 . (4.4.2)
. (4.4.2)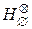 - склейки (операции
- склейки (операции 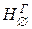 - склейки, если | V (
- склейки, если | V (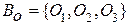 .
.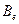 в качестве элементного базиса проводится аналогично теореме 4.4.2. Покажем, что операции
в качестве элементного базиса проводится аналогично теореме 4.4.2. Покажем, что операции 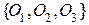 образуют операционный базис класса эйлеровых планарных графов. Установим вначале полноту указанного набора типов операций
образуют операционный базис класса эйлеровых планарных графов. Установим вначале полноту указанного набора типов операций 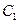 Î
Î 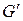 , состоящий из одной или нескольких компонент связности. Каждая из компонент является эйлеровым графом, так как степени их вершин сохранили четность после удаления ребер цикла Ci. Если компонента связности одна, то получаем представление
, состоящий из одной или нескольких компонент связности. Каждая из компонент является эйлеровым графом, так как степени их вершин сохранили четность после удаления ребер цикла Ci. Если компонента связности одна, то получаем представление 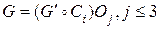 , в котором подграф
, в котором подграф 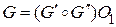 , где
, где 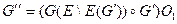 подграф, порожденный ребрами графа G, не принадлежащими
подграф, порожденный ребрами графа G, не принадлежащими 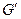 и
и 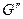 , являются эйлеровыми планарными, содержащими каждый не более чем по m -1 ребру, могут быть построены по предположению индукции.
, являются эйлеровыми планарными, содержащими каждый не более чем по m -1 ребру, могут быть построены по предположению индукции.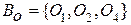 .
.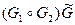 сохраняетгамильтоновость графов
сохраняетгамильтоновость графов 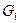 и
и 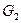 , если | V (
, если | V (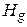 - склейки. Поскольку наличие кратных ребер не существенно для наличия гамильтонова цикла, то будем также пользоваться операциями
- склейки. Поскольку наличие кратных ребер не существенно для наличия гамильтонова цикла, то будем также пользоваться операциями 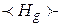 - склейки, сохраняющими и отсутствие кратных ребер. Простая цепь, содержащая n вершин, обозначается как Ln. Нижеследующие результаты получены в работе [10].
- склейки, сохраняющими и отсутствие кратных ребер. Простая цепь, содержащая n вершин, обозначается как Ln. Нижеследующие результаты получены в работе [10].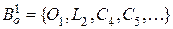 ,
, 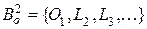 или
или 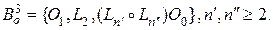 .
.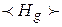 - склейки сохраняют эти свойства, то все графы, реализуемые операциями
- склейки сохраняют эти свойства, то все графы, реализуемые операциями 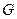 . Если граф
. Если граф 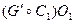 или
или 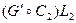 , где граф
, где граф 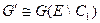 или
или 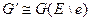 содержит на одну петлю С1 или на одно кратное ребро e меньше, чем граф
содержит на одну петлю С1 или на одно кратное ребро e меньше, чем граф 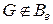 , содержащих
, содержащих 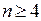 вершин. Пусть
вершин. Пусть 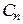 - гамильтонов цикл (один из гамильтоновых циклов) графа
- гамильтонов цикл (один из гамильтоновых циклов) графа 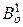 или
или  или
или 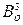 достаточно для построения простого гамильтонова графа
достаточно для построения простого гамильтонова графа 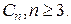
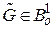 . При наличии в графе
. При наличии в графе 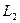 воспользуемся представлением
воспользуемся представлением 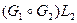 . Применяя далее это представление к гамильтоновым графам
. Применяя далее это представление к гамильтоновым графам 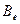 , либо к графам, не соде
, либо к графам, не соде


